Добавил:

d3YWMzbM Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский авиационный институт (национальный исследовательский университет)

Предмет:

Математический анализ

Файл:

ЛК Осипенко КЮ - весна 2021 (1 сем)

.pdf

Скачиваний:

Добавлен:

11.06.2021

Размер:

1.07 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 1313

121

									y				6
									1				q											q		y = x3





									O					q									q1														-		x



									1				q										q			y =							p

																																				x
																	Ðèñ. 78
Имеем																												∫0					dx ∫ px (								5xy + 11x2y2) dy
∫∫D (	5xy + 11x2y2) dxdy =																											∫0					dx ∫ px (								5xy + 11x2y2) dy
	4	9																										1									x3				4					9
										∫						(
										∫						(																					)
															1		2											3											x3
						=				0							5		xy2 +										11				x2y3							p		dx
										0							5												11											p	x	dx
						1				2							3															2					3
		=	∫0				(					x7 +											x11											x2 +						x3px dx
		=										x7 +											x11											x2 +						x3px dx
										5							11															5					11						)		1
							1										1															2							2						1

																																									x9=2) 0
		= (									x8 +										x12														x3		+
		= (						20			x8 +							44			x12											15			x3		+	33
																	1															1					2				2					1					1
																					=							+											+				=						+			= 0:
																					=	20						+			44						15		+		33		=				12		+		12	= 0:
Задача 3. Вычислить криволинейный интеграл
∫ (x2 + y) dx + (x								y2) dy;																	= [AB : y = 3 + x2; A(0; 3); B(2; 7):
Имеем																												(																								)
							2																					(																								)
∫ (x2+y) dx+(x y2) dy = ∫0 2																												x2				+ 3 + x2 + (x (3 + x2)2)2x dx
		= ∫0								(																				2													)
		= ∫0										3 18x + 4x2																							12x3						2x5			dx
		4															1																						32							64						266

= (3x	9x2 +			3	x3						3x4									3	x6) 0											= 6					36+				3		48					3		=		3	:
Задача 4. Найти d2z: z = √
Задача 4. Найти d2z: z = √																											3xy								y2.

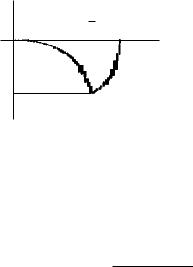
122

Имеем

zx′

;

√

′

3xy

zy =

;

2√

3xy9y2y2

zxx′′

;

4(3xy

y2)3=2

zxy′′

(

y(3x

2y)

)

9xy

;

2(3xy

y2)3=2

4(3xy

y2)3=2

√

3xy

zyy′′

(3x 2y)2

9x2

√

4(3xy

y2)3=2

4(3xy

y2)3=2

3xy

Следовательно,

d2z = z′′ dx2 + 2z′′

dxdy + z′′ dy2 =

9 (y2dx2

2xydxdy + x2dy2)

4(3xy

y2)3=2

Задача 5. Изменить порядок интегрирования в повторном интеграле:

p
p	3	0		2			0
∫0		dx ∫p		2 f(x; y) dy + ∫p		dx ∫	p		f(x; y) dy:
∫0		dx ∫p	4 x2	2 f(x; y) dy + ∫p	3	dx ∫	p	4 x2

Нарисуем сначала область интегрирования.

y 6	p3q	2q -x
Oq	p3q	2q -x
1 q	q

Ðèñ. 79

Чтобы написать повторный интеграл в другом порядке, надо написать уравнение левой кривой и правой кривой. Левая кривая

часть окружности (y+2)2 +x2 = 4. Учитывая, что это правая часть

√

этой окружности, получаем x = 4 (y + 2)2. Правая кривая это часть окружности x2 + y2 = 4. Так как рассматриваемая часть

123

является правой частью окружности, x = 4 x2. Таким образом,

получаем		p

				2
	∫ 0	dy ∫p	4	x	f(x; y) dx:
	∫ 0	dy ∫p		(y+2)2	f(x; y) dx:
	1		4	(y+2)2

Задача 6. Найти точки экстремума функции z = 2x3 + 3y2 24x + 6y + 5. Указать тип экстремума.

Найдем стационарные точки

	zx′ = 6x2 24 = 0;
	zy′ = 6y + 6 = 0:
Таким образом, имеем две точки: (2; 1) è ( 2;		1). Посчитаем
производные второго порядка
	zxx′′ = 12x;
	zxy′′ = 0;
	zyy′′ = 6:
Äëÿ ∆ = zxx′′	zyy′′ (zxy′′ )2 получаем: ∆ > 0 в точке (2;	1) è ∆ < 0 â
точке ( 2;	1). Следовательно, в точке ( 2; 1) экстремума нет, а

в точке (2; 1) экстремум есть, причем там локальный максимум, т.к. zxx′′ > 0.

Задача 7. Найти объем тела, ограниченного поверхностями
x2 + y2 = y; x2 + y2 = 4y; z = 3√x2 + y2; z = 0:
		z 6
AA		q12
	AAAA		4 -
		A	4 -
			y

x

Ðèñ. 80

Проекция тела на плоскость Oxy представляет собой круг с цен-

2	2	из которого вырезан
тром в точке (0; 2) радиуса 2: x + (y	2) 4,
		2	+ (y	1=2)	2	1=4.
круг с центром в точке (0; 1=2) радиуса 1=2: x

А само тело цилиндр с этим основанием и верхней поверхностью

124

√

конуса z = 3 x2 + y2. Для вычисления объема перейдем к цилин-

дрической системе координат. Тогда цилиндры, в основаниях которых лежат описанные выше круги, будут задаваться уравнениями

= sin φ; = 4 sin φ;

àконус уравнением z = 3 .

Имеем

dxdydz = ∫0

dφ

∫sin φ

d ∫0

jV j =

∫∫∫V

∫

4 sin φ

∫

4 sin φ

0 3

dφ

sin φ

3 2 d =

sin φ

dφ =

63 sin3 φ dφ

∫

(

)

(1 cos2 φ) d cos φ =

cos φ

cos3 φ

= 84:

Задача 8. а) Найти наибольшее и наименьшее значения

ôóíê-

öèè z = x2

y2 в круге x2 + y2 4.

Найдем стационарные точки

zx′ = 2x; zy′ = 2y:

Стационарная точка (0; 0). Далее,

∆ = zxx′′ zyy′′

(zxy′′ )2 = 4 < 0:

Тем самым экстремумов внутри круга нет. Исследуем функцию на границе круга. Зададим окружность параметрически

x = 2 cos t; y = 2 sin t:

Тогда

z = 4 cos 2t:

Следовательно, наибольшее значение 4 достигается в точках ( 2; 0), а наименьшее 4 в точках (0; 2).

б) Найти наибольшее и наименьшее значения функции z = x2 + 2xy 4x + 8y в прямоугольнике 0 x 1, 0 y 2.

Найдем стационарные точки

zx′ = 2x + 2y 4 = 0; zy′ = 2x + 8 = 0:

Стационарная точка ( 4; 6). Эта точка не принадлежит прямо-

угольнику. Найдем наибольшее и наименьшее значения функции на сторонах прямоугольника. При x = 0; 1 z линейная функция,

а линейная функция достигает наибольшего и наименьшего значе- ний на концах отрезка. При y = 0; 2 z параболы, но их вершины

125

находятся вне интервала (0; 1). Поэтому наибольшее и наименьшее

значения функции находятся в вершинах прямоугольника. Посчи- таем значения в вершинах

z(0; 0) = 0; z(1; 0) = 3; z(1; 2) = 17; z(0; 2) = 16:

Итак, наибольшее значение 17 достигается в точке (1; 2), а наименьшее 3 в точке (1; 0).

Задача 9. Вычислить тройной интеграл:

∫∫∫

x2y dxdydz;

по области V , если область ограничена поверхностями

x2 + y2 + z2 = 4; x = 0; y = 0; z = 0 (x 0; y 0; z 0):

Легко понять, что V шар радиуса 2, находящийся в первом октанте. Перейдем к сферической системе координат

x = r sin cos φ; y = r sin sin φ; z = r cos :

Тогда

∫∫∫

x2y dxdydz

∫0

dφ

(r sin cos φ)2r sin sin φr2 sin dr

= ∫0

=2 cos2 φ sin φ dφ ∫0

=2 sin4 d ∫0

2 r5 dr

cos 2 )2

∫0

cos2 φ d cos φ

∫0

8 cos3 φ

∫

(

1 +

cos 4

) =2

2 cos 2 +

sin 4

(

sin 2 +

) 0

Задача 10. Вычислить ∫

(x + 2y) dl;

ãäå L : x2 + y2 = 9y.

126

Кривая L окружность с центром в точке (0; 4; 5) и радиусом

4; 5: x2 + (y		4; 5)2 = 4; 52. Зададим L в параметрическом виде
		x(t) = 4; 5 cos t;				t 2 [0; 2 ]:
		y(t) = 4; 5 + 4; 5 sin t;
Тогда			√
	2
∫L(x + 2y) dl = ∫0 2 (x(t) + 2y(t))					x′2(t) + y′2(t)			dt
= ∫0						√
	(4; 5 cos t + 2(4; 5 + 4; 5 sin t))						4; 52 sin2 t + 4; 52 cos2 t dt
		= 4; 52	∫0	2		(cos t + 2 + 2 sin t) dt = 81 :

81. Вопросы к экзамену по математическому анализу

(2021 ãîä)

1.Множества. Операции над множествами, их свойства. Множество действительных чисел, его подмножества.

2.Числовая последовательность, способы задания. Монотонность, ограниченность. Предел последовательности, определение и свойства. Теорема Вейерштрасса.

3.Предел функции в точке и на бесконечности. Свойства пределов. Односторонние пределы.

4.Первый замечательный предел и его следствия. Второй заме- чательный предел и его следствия.

5.Основные теоремы о пределах. Бесконечно малые, бесконечно большие и их свойства. Связь определения предела с бесконечно малыми. Сравнение бесконечно малых.

6.Непрерывность функции в точке и на отрезке. Точки разрыва

èих классификация. Свойства функций, непрерывных в точке и на отрезке.

7.Производная, ее геометрический и механический смысл. Уравнение касательной. Свойства производной (правила дифференцирования).

8.Производная сложной, обратной, неявной и параметрически заданной функции. Таблица основных производных. Дифференцируемость функции, ее связь с непрерывностью. Дифференциал функции, его геометрический смысл.

9.Теоремы Ферма, Ролля, Лагранжа и Коши. Правило Лопита-

ëÿ.

10.Формула Тейлора. Разложение основных элементарных функций по формуле Тейлора.

127

11.Условия возрастания и убывания функции. Экстремумы: определение, необходимое условие. Достаточные условия экстремума.

12.Выпуклость вверх и вниз: определение, связь с производными. Точки перегиба: определение, необходимое и достаточное условия существования.

13.Асимптоты графика функции: виды и способы нахождения. Общая схема исследования функции. Производные и дифференциалы высших порядков, их свойства.

14.Комплексные числа, их изображение на плоскости. Алгебра- ические операции над комплексными числами. Комплексное сопряжение. Модуль и аргумент комплексного числа. Алгебраическая и тригонометрическая формы комплексного числа. Формула Муавра. Корни из комплексных чисел. Формула Эйлера. Показательная форма комплексного числа.

15.Многочлены и их корни. Теорема Безу. Основная теорема алгебры. Разложение многочлена на множители в комплексной и действительной области. Рациональные дроби. Правильная рациональная дробь, ее разложение в сумму простейших в комплексной

èдействительной области.

16.Первообразная и ее свойства. Определение неопределенного интеграла. Свойства неопределенного интеграла. Таблица основных интегралов. Замена переменной в неопределенном интеграле. Формула интегрирования по частям.

17.Интегрирование рациональных дробей.

18.Интегрирование дробно-линейных и квадратичных иррациональностей.

19.Интегрирование рациональных тригонометрических выражений и выражений вида sinn x cosm x.

20.Понятие интегральной суммы. Определение определенного интеграла. Ограниченность интегрируемой функции. Свойства определенного интеграла.

21.Интегрируемость кусочно-непрерывных и монотонных функций. Производная определенного интеграла по переменному верхнему пределу. Формула Ньютона-Лейбница.

22.Замена переменной и интегрирование по частям в определенном интеграле. Объем тела и площадь поверхности вращения.

23.Площадь фигуры в декартовых и полярных координатах. Длина кривой, заданной параметрически, а также в виде графика функции в декартовых или полярных координатах.

24.Несобственные интегралы 1 и 2 рода: определение, понятие сходимости, признак сравнения. Признак сравнения в предельной форме. Абсолютная и условная сходимость несобственных интегралов.

128

25.Определение числового ряда, частичной суммы, сходимости ряда. Простейшие свойства сходящихся рядов. Необходимое условие сходимости ряда. Остаток ряда, его связь со сходимостью. Критерий Коши сходимости числового ряда.

26.Ограниченность частичных сумм как условие сходимости знакоположительных рядов. Признаки сравнения. Интегральный признак Коши.

27.Признак Даламбера. Радикальный признак Коши. Знакопеременные ряды. Признак Лейбница. Абсолютная и условная сходимость. Свойства абсолютно сходящихся рядов.

28.Определение функционального ряда, область сходимости, сумма функционального ряда. Равномерная сходимость функциональных рядов. Признак Вейерштрасса. Свойства равномерно сходящихся рядов.

29.Степенные ряды. Теорема Абеля. Определение радиуса и интервала сходимости степенного ряда. Формулы Даламбера и КошиАдамара. Почленное дифференцирование и интегрирование степенных рядов.

30.Разложение функции в степенной ряд. Ряды Тейлора и Маклорена. Разложение в ряд Маклорена основных элементарных функций. Формула Эйлера.

31.Функция нескольких переменных. Геометрическое изображение функции двух переменных. Линии и поверхности уровня. Предел функции нескольких переменных. Свойства пределов. Непрерывность функции нескольких переменных, свойства непрерывных функций.

32.Частные производные, их свойства и геометрический смысл. Дифференцируемость функции нескольких переменных. Дифференциал, его геометрический смысл и свойства. Применение дифференциала к приближенным вычислениям.

33.Дифференцирование сложных функций. Инвариантность формы дифференциала. Неявные функции, условия их существования. Дифференцирование неявных функций.

34.Производная по направлению. Градиент и его свойства. Касательная плоскость и нормаль к поверхности.

35.Частные производные и дифференциалы высших порядков. Формула Тейлора для функции нескольких переменных.

36.Экстремумы функций нескольких переменных. Необходимое условие экстремума. Достаточное условие экстремума. Критерий Сильвестра.

37.Условный экстремум. Метод множителей Лагранжа. Нахождение наибольших и наименьших значений функции в ограниченной замкнутой области.

38.Двойной и тройной интеграл, их определение и свойства. Геометрический смысл двойного интеграла.

129

39.Вычисление двойного и тройного интегралов сведением к повторным.

40.Замена переменных в кратных интегралах. Якобиан, его геометрический смысл. Вычисление двойного интеграла в полярных координатах. Примеры.

41.Вычисление тройного интеграла в цилиндрической и сфери- ческой системах координат. Примеры.

42.Криволинейный интеграл 1-го рода: определение, свойства. Вычисление криволинейного интеграла 1-го рода для кривых, заданных параметрически, в декартовых или полярных координатах.

43.Криволинейный интеграл 2-го рода: определение, свойства, способ вычисления. Условия независимости криволинейного интеграла 2-го рода от пути интегрирования. Формула Грина.

44.Поверхностный интеграл 1-го рода: определение, свойства, способ вычисления.

45.Поверхностный интеграл 2-го рода: определение, свойства, способ вычисления.

46.Элементы теории поля. Формула Гаусса-Остроградского. Формула Стокса.

47.Геометрические и физические приложения кратных, криволинейных и поверхностных интегралов.

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 1313