Добавил:

d3YWMzbM Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский авиационный институт (национальный исследовательский университет)

Предмет:

Математический анализ

Файл:

ЛК Осипенко КЮ - весна 2021 (1 сем)

.pdf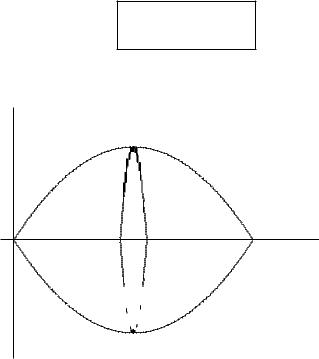

Скачиваний:

Добавлен:

11.06.2021

Размер:

1.07 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 133 4 5 6 7 8 9 10 11 12 13 > Следующая >>>

Если вращать криволинейную трапецию, которая соответствует этой функции, то получится тело вращения. В каждой точке x 2 [a; b] легко посчитать площадь сечения это площадь круга

радиуса R = f(x). Тем самым S(x) = f2(x). Следовательно, объем

этого тела вращения равен

∫ b

V = f2(x) dx:

Пример 7. Вычислить объем тела, полученного вращением одной арки синусоиды.

y 6

y = sin x

0					x

Ðèñ. 28

Имеем				∫				(		)
	∫			∫				(		)		2
V =	0			0		cos 2x) dx =		x	sin22x	0	=	2
V =	0	sin2 x dx =	2	0	(1	cos 2x) dx =	2	x	sin22x	0	=	2 :

6. Вычисление объема тел вращения, когда образующая задана

параметрически. Пусть образующая задана в виде

{

y = y(t);

t :

x = x(t);

Если бы она задавалась в виде y = f(x), то объем вычислялась бы

по формуле ∫ b

V = f2(x) dx:

Сделаем в этом интеграле замену x = x(t). Тогда

∫

V = f2(x(t)) dx(t):

Òàê êàê f(x(t)) = y(t), то получаем формулу

∫

V = y2(t)x′(t) dt:

Лекция 2 марта 2021 г.

7. Вычисление длины дуги кривой. Пусть кривая задана функцией y = f(x) на отрезке [a; b]. Разобьем отрезок [a; b] íà n частей

точками a = x0 < x1 < x2 : : : < xn = b. И заменим вычисление длины дуги на каждом из кусков вычислением длины хорды ∆lk.

y 6

				y = f(x)
		,			Q
	,	,			Q
%	,				QQ
%%
						-
0 a x1 x2 x3					xn 1 b		x
					Ðèñ. 29
Тогда
n			n			n	∆2yk
L ∆lk =					∆2xk + ∆2yk =	√1 +	∆2yk	∆xk:
L ∆lk =					∆2xk + ∆2yk =	√1 +	∆2xk	∆xk:
=1			k=1			=1
∑k			∑√			∑k

					∆lk ∆yk
				∆xk
				∆xk
						-
		xk 1			xk	x
					Ðèñ. 30
По теореме Лагранжа существует точка k 2 [xk							1; xk] такая, что
∆yk = f(xk) f(xk 1) = f′( k)(xk						xk 1) = f′( k)∆xk:

Следовательно,

∆2yk = f′2( k): ∆2xk

Отсюда

∑√

√

lim

∫a

f 2

dx:

= d(T )!0 k=1

1 +

′

( k)∆

k =

1 +

′

( )

Тем самым

L = ∫ab

√

1 + f′2(x) dx:

(2)

8. Вычисление длины дуги параметрически заданной кривой. Пусть кривая y = f(x) задана параметрически

y = y(t);

{x = x(t);

t :

Тогда

f′(x) =

y′(t)

x′(t)

Сделав в формуле (2) замену x = x(t), будем иметь

∫

√

√1 +

y 2(t)

L =

′

x′(t) dt =

x′2(t) + y′2(t) dt:

x′2(t)

Тем самым получена формула

L = ∫

√

x′2(t) + y′2(t) dt:

(3)

В случае пространственной кривой

y = y(t);

8x = x(t);

t ;

имеет место

<z = z(t);

аналогичная формула

L = ∫

√

x′2(t) + y′2(t) + z′2(t) dt:

Пример 8. Найти длину одной арки циклоиды

y = R(1

cos t);

{x = R(t

sin t);

0 t 2 :

y 6
'PiR	$
Pq
&%		-
0		2 R x

Ðèñ. 31

Имеем

∫0

2 √

dt = ∫0

2 √

L =

x′2(t) + y′2(t)

R2(1 cos t)2 + R2 sin2 t

= R ∫0

dt = R ∫0

2 p

2 cos t + cos2 t + sin2 t

2 cos t dt

∫

√

∫

(

)

√4 sin2

= R

dt = 2R

sin

dt = 4R

cos

= 8R:

9. Вычисление длины дуги кривой, заданной в полярной системе координат. Пусть кривая задана в полярной системе координат

= (φ); φ :

От задания кривой в полярной системе координат можно перейти

к заданию той же кривой в параметрическом виде

{

y = (φ) sin φ;

φ :

x = (φ) cos φ;

Имеем

y′(φ) = ′(φ) sin φ + (φ) cos φ; x′(φ) = ′(φ) cos φ (φ) sin φ:

Поэтому

x′2(φ) + y′2(φ) = ′2(φ) + 2(φ):

Учитывая формулу (3), получаем

∫ √

L = ′2(φ) + 2(φ) dφ:

Пример 9. Найти длину кардиоиды = a(1 + cos φ), 0 φ 2 .

y	6
y	6

a
a
			-
			-
	0	2a	x

Ðèñ. 32

Имеем

L = 2 ∫0

√

dφ

a2 sin2 φ + a2(1 + cos φ)2

√

= 2a ∫0

√

∫0

sin2 φ + 1 + 2 cos φ + cos2

φ dφ = 2a

2(1 + cos φ) dφ

∫

= 4a

cos

dφ = 8a sin

= 8a:

9. Несобственные интегралы с бесконечными пределами

Пусть дана функция f(x), непрерывная на промежутке [a; +1).

Для любого b a существует интеграл

∫ b

f(x) dx:

y 6

y = f(x)

						-
	0 a				b	x
			Ðèñ. 33
Определение 6.		Несобственным интегралом называется
	∫		+1 f(x) dx = lim	∫	b f(x) dx:

b!+1 a

Если этот предел существует, то говорят, что несобственный интеграл сходится. В противном случае говорят, что несобственный интеграл расходится.

Пусть функция f(x), непрерывная на промежутке ( ; a]. Тогда аналогичным образом определяется несобственный интеграл

∫	a						a
	f		x		dx	lim	f		x		dx:
		(		)		= b!	∫b	(		)

Если функция f(x) непрерывна на всей числовой оси, то

∫ +1 ∫ c ∫ +1

f(x) dx = f(x) dx + f(x) dx:

Нетрудно убедиться, что это определение не зависит от точки c.

10. Обобщенная формула Ньютона Лейбница

Пусть функция f(x) непрерывна на промежутке [a; +1) è F (x)

ее первообразная. Тогда

∫a	+1 f	x		dx def	lim	b
∫a	(		)	=	b!+1	∫a

f(x) dx = lim (F (b)	F (a))
b!+1
=	lim F (b) F (a):
	b!+1

Положив

F (+1) = lim F (b);

b!+1

получаем	∫a+1 f(x) dx = F (+1) F (a):
	∫a+1 f(x) dx = F (+1) F (a):
Эта формула, которую можно записывать и в виде
	∫		+
		a+1 f(x) dx = F (x) a 1;		Лейбница.
носит название обобщенной формулы Ньютона				Лейбница.

Аналогичные формулы имеют место и для двух других типов

интегралов:					f(x) dx = F (x) a
			a		f(x) dx = F (x) a					;
		∫+		1				+		1
				1						1
		∫
		∫							интеграл
Примеры. Вычислить несобственный									интеграл
					f(x) dx = F (x)					:
	1:				∫	+1
						+1	dx	:

							x2 + 1

y =

x2+1

Ðèñ. 34

Имеем

2: При каких сходится несобственный

интеграл

∫

x2 + 1

= arctg x

(

2 ) = :

∫1

dx?

y =

Ðèñ. 35

Имеем

1 1; ̸= 1;

+1 1

+ 1

∫

dx =

Òàê êàê

то интеграл

расходится при

ln x 1

;

= 1:

limx

ln x = +

= 1

+1 < 0. Поэто-

Предел limx!+1 x

существует только при

му интеграл сходится только при > 1.

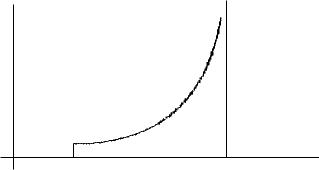
11. Несобственные интегралы от неограниченных функций

Пусть дана функция f(x), непрерывная на промежутке [a; b), но неинтегрируема на отрезке [a; b] (например, f(x) ! 1 ïðè x ! b). Точка b в таком случае называется особой.

y 6

y = f(x)

Ðèñ. 36

Определение 7. Несобственным интегралом называется

∫ b ∫ c

f(x) dx = lim f(x) dx:

ac!b 0 a

Если функция f(x) непрерывна на промежутке (a; b], а точка a

является особой, то несобственный интеграл определяется следующим образом ∫ b ∫ b

f(x) dx = lim f(x) dx:

ac!a+0 c

Если обе точки a è b являются особыми, то

b						∫c	b	c
f		x		dx	lim		f(x) dx + lim	f(x) dx:
∫a	(		)		= c!a+0		c!b 0	∫a

Терминология, связанная со сходимостью, остается такой же, как для несобственных интегралов с бесконечными пределами.

12. Обобщенные формулы Ньютона Лейбница для интегралов от неограниченных функций

Пусть функция f(x) непрерывна в промежутке [a; b) и имеет в точке b особенность. Предположим, что F (x) первообразная функции f(x). Тогда

b				dx def		c
f		x		dx def	lim	f(x) dx
∫a	(		)	=	c!b 0	∫a
						= lim (F (c)		F (a)) = lim	F (c) F (a):
						c!b	0	c!b	0
Обозначив F (b					0) = limc!b		0 F (c), получаем формулу, которая

называется обобщенная формула Ньютона Лейбница

∫ b

f(x) dx = F (b 0) F (a):

Ее также записывают в виде

∫			b	0
	ab f(x) dx = F (x) a			:
Аналогичные формулы имеют место и				для функций, имеющих

особенности в точке a или в обеих точках a è b:
∫		b
∫		b		0
	ab f(x) dx = F (x) a+0;
	b
∫
∫
	a
	a	f(x) dx = F (x) a+0:

Пример 10. При каких сходится интеграл

∫ 1 1

0 x

dx?

y 6

y =

Ðèñ. 37

Имеем

;

̸= 1;

1 1

+ 1

0+0

∫

dx =

Òàê êàê

,>то интеграл расходится при

<ln x 0+0;

= 1:

limx 0+0 ln x =

= 1

Предел limx!0+0 x

существует только при +1 > 0. Поэто-

му интеграл сходится только при < 1 (при 0 рассматриваемый интеграл не является несобственным).

<<< < Предыдущая 1 23 / 133 4 5 6 7 8 9 10 11 12 13 > Следующая >>>