
ЛК Осипенко КЮ - весна 2021 (1 сем)
.pdf
Лекция 9 февраля 2021 г.
1. Задачи, приводящие к понятию определенного интеграла
Обсудим сначала понятие площадь . Всем хорошо знакомо, что площадь прямоугольника со сторонами a è b равна ab. ×òî ýòî
означает? Если длины сторон мы измеряли в сантиметрах, то фактически это означает, что в прямоугольнике размещается ab êâàä-
ратиков со стороной 1см. Это число, конечно, может быть и не
целым, тогда там разместятся не целые квадратики, а какие-то их части.
А как быть с параллелограммом?
|
|
B |
a |
|
B′ |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
A |
C |
|
A′ C′ |
||||||
Ðèñ. 1
Так как площади треугольников ABC è A′B′C′ равны, то все сводится к вычислению прямоугольника CBB′C′, а его площадь равна ah.
Теперь займемся вычислением площади треугольника.
ZpppppppppppppppppppppZ |
pp |
p |
||||
ph |
ZZZ |
a |
|
pppp |
|
|
B |
|
|
|
B′ |
||
|
|
ZZZ |
ppppppp |
|
|
|
A |
|
Cp |
|
|
|
|
|
|
|
p |
|
|
|
Ðèñ. 2
Достроим треугольник ABC до параллелограмма ABB′C. ßñíî,
что площадь параллелограмма равна удвоенной площади треугольника, а площадь параллелограмма мы умеем находить. Она равна ah. Поэтому площадь треугольника равна
12ah:
1

2
Тем самым можно найти площадь любой фигуры, которая может быть разбита на треугольники. Например, площадь трапеции.
|
pp |
p |
b |
|
AA |
|
|
|
|
B |
|
|
C |
|
|
||
|
|
|
|
|
|
|
||
|
h ppppppp |
ppppp |
AA |
ApA |
||||
|
|
|
|
ppp |
||||
|
|
|
|
|
|
|
|
p |
A |
|
a |
|
|
|
pD |
||
Ðèñ. 3
Разбиваем трапецию ABCD на два треугольника ABC è BCD. Площадь каждого из них известна, поэтому получаем
ah2 + bh2 = a +2 bh:
А как быть с кругом. Здесь уже не обойтись без понятия предела. В круг радиуса R вписывается правильный n-угольник. Пло-
щадью круга называется предел площадей правильных вписанных n-угольников при n ! 1. Площадь каждого из треугольников,
на которые разбивается правильный вписанный n-угольник легко
посчитать
Sn = 12R2 sin 2n
(эта еще одна формула для площади треугольника, выражающая площадь через длину сторон и угол между ними, и которая непосредственно выводится из полученной нами выше). Вспоминая первый замечательный предел, получаем формулу для площади круга радиуса R
S = lim n12R2 sin 2n = R2:
Рассмотри теперь более общую ситуацию. Пусть задана функция y = f(x) > 0 на отрезке [a; b]. Множество точек между графиком
этой функции и осью Ox называется криволинейной трапецией.
Как вычислить площадь данной криволинейной трапеции. Давайте разобьем отрезок [a; b] íà n кусков точками a = x0 < x1 < : : : <
xn = b. В каждом куске [xk 1; xk] выберем точку k. Заменим кусок криволинейной трапеции между точками xk 1 è xk на прямоуголь- ник с основанием ∆xk = xk xk 1 и высотой f( k) (см. рис. 4). Площадь каждого такого прямоугольника равна f( k)∆xk. Поэто- му приближенное выражение для площади равно
e ∑n
S = f( k)∆xk:
k=1
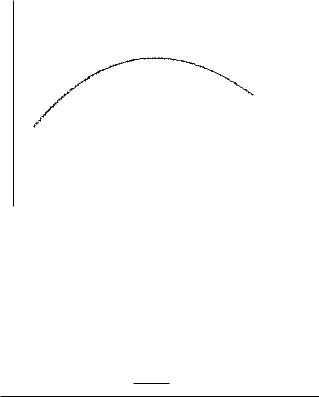
3
y 6
y = f(x)
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 a 1 x1 2 x2 3 x3 |
xn 1 n b |
x |
|||||||||||
Ðèñ. 4
На самом деле это и есть определение площади криволинейной трапеции (надо только уточнить, что понимается под пределом).
Рассмотрим еще одну задачу, приводящую к вычислению предела подобных сумм.
aq |
1q |
xq1 q |
F (x) |
xnq |
1 qn bq |
|
2 xq2 q3 xq3 - |
- |
Ðèñ. 5
Предположим, что материальная точка перемещается из a â b по отрезку [a; b] под действием силы F (x), которая направлена параллельно отрезку [a; b], но значение которой, вообще говоря, ме-
няется от точки к точке. Требуется вычислить работу. Поступим следующим образом. Снова разобьем [a; b] íà n кусков точками
a = x0 < x1 < : : : < xn = b. В каждом куске [xk 1; xk] выберем точку k. Если считать, что на каждом маленьком отрезке сила мало меняется и приближенно равна силе в некоторой внутренней точке, то работа на каждом отрезке приближенно равна F ( k)∆xk. Поэтому приближенное выражение для работы равно
e ∑n
A = F ( k)∆xk:
k=1
Чем больше мы измельчаем рассматриваемый отрезок, тем точ- нее мы вычисляем работу. И снова мы приходим к необходимости вычислять предел суммы, подобной той, которая встретилась при вычислении площади криволинейной трапеции.
2. Определенный интеграл
Начнем с ряда определений.

4
Определение 1. Разбиением отрезка [a; b] будем называть систему точек a = x0 < x1 < : : : < xn = b и точек k 2 [xk 1; xk], k = 1; : : : ; n.
aq |
1q |
xq1 q2 xq2 q3 xq3 |
xnq |
1 qn bq |
- |
Ðèñ. 6
Будем обозначать разбиения буквой T .
Определение 2. Диаметром разбиения T называется величина
d(T ) = max ∆xk; ∆xk = xk xk 1:
1 k n
Пусть дана функция f(x) на отрезке [a; b], è T некоторое раз-
биение этого отрезка. |
|
Определение 3. Интегральной суммой для разбиения T называ- |
|
ется величина |
∑k |
|
n |
S(T ) = |
f( k)∆xk: |
|
=1 |
Определение 4. Число I называется пределом интегральных |
|
ñóìì S(T ) ïðè d(T ) ! 0 |
|
I = |
lim S(T ); |
d(T )!0
если для любого " > 0 найдется > 0 такое, что при d(T ) < выполняется неравенство
jI S(T )j < ":
Определение 5. Пусть задана функция f(x) на отрезке [a; b]. Определенным интегралом от функции f(x) îò a äî b называется
|
∑ |
|
|
|
b |
n |
|
|
|
f(x) dx |
lim |
f( )∆x |
: |
|
∫a |
= d(T )!0 k=1 |
k |
k |
|
Теорема 1 (о существовании определенного интеграла) . Äëÿ ëþ-
бой функции f(x), непрерывной на отрезке [a; b], определенный ин- теграл ∫ab f(x) dx существует.
3. Свойства определенного интеграла
Далее считаем, что все встречающиеся функции непрерывны на отрезке [a; b], и, следовательно, соответствующие интегралы суще-
ствуют. |
∫ a |
1. |
def
f(x) dx = 0:
a
5
2. Пусть a > b.
|
|
|
|
|
|
|
|
∫a |
b |
|
def |
∫b |
a |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
f(x) dx = |
f(x) dx: |
|
|
|
|
|||||||||
3. |
|
|
|
|
|
|
|
|
|
∫ab |
1 dx = b |
|
a: |
|
|
|
|
|
||||
Доказательство. |
|
|
∑ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 dx |
|
lim |
|
x |
|
|
|
lim (b |
a) = (b |
a): |
|||||||||
|
|
∫a |
|
|
|
= d(T )!0 k=1 |
|
∆ k = d(T )!0 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. |
|
|
|
|
|
|
|
∫ab Cf(x) dx = C ∫ab f(x) dx: |
|
|
|
|
||||||||||
Доказательство. |
|
|
∑ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
Cf(x) dx |
|
|
|
lim |
Cf( |
)∆x |
|
|
|
|
|
|
|
|
||||||||
∫a |
|
|
|
|
= d(T )!0 k=1 |
|
k |
|
|
k |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑ |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
C lim |
|
|
|
f( )∆x |
|
= C |
f(x) dx: |
||||
|
|
|
|
|
|
|
|
|
|
= |
|
d(T )!0 k=1 |
k |
k |
|
|
∫a |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. |
|
|
∫ab(f(x) + g(x)) dx = ∫ab f(x) dx + ∫ab g(x) dx: |
|||||||||||||||||||
Доказательство. |
|
|
|
|
∑ |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
b |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
∫a ( |
f |
x |
|
g |
x |
|
|
dx |
|
lim |
|
|
(f( ) + g( ))∆x |
|
|
|||||||
( |
|
) + |
( |
|
)) |
|
= d(T )!0 k=1 |
|
|
k |
|
k |
|
|
k |
|
||||||
|
|
|
|
|
|
|
|
|
∑ |
|
|
|
|
|
|
∑k |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
= |
|
|
lim |
|
f( k)∆xk + |
|
lim |
g( k)∆xk |
||||||||||
|
|
|
|
|
d(T )!0 k=1 |
|
|
|
d(T )!0 |
=1 |
|
|
|
∫ab g(x) dx: |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ∫ab f(x) dx + |
|||||
6. Пусть a < c < b. Тогда
∫ b ∫ c ∫ b
f(x) dx = f(x) dx + f(x) dx:
a |
a |
c |

6
y 6
y = f(x)
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 a |
c |
|
b |
x |
||||
Ðèñ. 7
Доказательство. Добавим в каждом разбиении T точку c â ñè-
стему точек fxkg (если ее не было в исходном разбиении). Новое разбиение обозначим через T ′. Очевидно, что диаметр разбиения
при этом не увеличится d(T ) d(T ′). Поэтому
∫ b
a
|
∑k |
|
|
|
|
|
∑ |
|
|
|
n |
|
|
|
|
|
n |
|
|
f(x) dx = lim |
f( k)∆xk = lim |
|
f( k)∆xk |
||||||
d(T )!0 |
=1 |
|
|
|
|
d(T ′)!0 k=1 |
|
||
|
∑ |
|
|
|
|
∑ |
|
|
|
|
n1 |
|
|
|
|
n |
|
|
|
lim |
|
f |
|
x |
|
|
f |
|
x |
= d(T ′)!0(k=1 |
( |
k)∆ |
|
k + k=n1+1 |
( |
k)∆ k) |
|||
∑ |
|
|
|
|
k=∑1 |
|
|||
n1 |
|
|
|
|
|
n |
|
|
|
= lim |
f( k)∆xk + |
lim |
|
|
f( k)∆xk |
||||
d(T ′)!0 k=1 |
|
|
|
|
d(T ′)!0 |
n +1 |
|
||
|
|
|
|
|
|
= ∫ |
c f(x) dx + ∫ b f(x) dx: |
||
a |
c |
|
|
7. Для любого расположения точек a, b è c |
|
∫ b ∫ c ∫ b
f(x) dx = f(x) dx + f(x) dx:
a a c
Доказательство. Пусть, например, c < a < b.
cq |
aq |
|
Ðèñ. 8 |
bq |
- |
Тогда по доказанному в предыдущем пункте |
|||||
∫ |
b f(x) dx = |
∫ |
a f(x) dx + |
∫ |
b f(x) dx: |
c |
c |
a |
|
7 |
Отсюда |
∫c a f(x) dx + ∫c b f(x) dx = ∫ac f(x) dx + ∫c b f(x) dx: |
∫ab f(x) dx = |
|
|
|
8.Åñëè f(x) 0 ïðè x 2 [a; b], òî
∫b
f(x) dx 0:
a
Доказательство.
|
|
|
|
|
∑ |
|
|
|
b |
|
|
|
|
n |
|
|
|
f |
|
x |
|
dx |
lim |
f( )∆x |
: |
|
∫a |
( |
|
) |
|
= d(T )!0 k=1 |
k |
k |
|
Òàê êàê f( k) 0 è ∆xk 0, òî
∑n
f( k)∆xk 0
k=1
для любого разбиения T . Поэтому и ее предел неотрицательный.
9. Åñëè f(x) g(x) ïðè x 2 [a; b], òî
∫ b ∫ b
f(x) dx g(x) dx:
aa
Доказательство. Так как f(x) |
g(x) 0, то из предыдущего пунк- |
||
та следует, что |
∫ab(f(x) |
|
|
Следовательно, |
g(x)) dx 0: |
||
∫ b f(x) dx |
∫ b g(x) dx 0: |
||
|
|||
|
a |
a |
|
|
|
|
|
10. Åñëè m f(x) M ïðè x 2 [a; b], òî
∫ b
m(b a) f(x) dx M(b a):
a
Доказательство. Из предыдущего пункта получаем
∫ b ∫ b ∫ b
m dx f(x) dx M dx:
a a a
Из свойств 4 и 3 следует, что
∫ b ∫ b
m dx = m 1 dx = m(b a):
aa

8
Аналогично ∫ b |
∫ b |
|
M dx = M 1 dx = M(b a): |
a |
a |
|
|
11. |
|
Теорема 2 (теорема о среднем). Пусть функция f(x) непрерывна
на отрезке [a; b]. Тогда найдется точка 2 [a; b] такая, что
∫ b
f(x) dx = f( )(b a):
a
y 6
y = f(x)
|
|
|
|
|
|
- |
|
0 a |
|
b |
x |
||||
Ðèñ. 9
Доказательство. Непрерывная функция на отрезке достигает своего минимального значения m и своего максимального значения M.
Тем самым m f(x) M ïðè x 2 [a; b]. Следовательно, из свой-
ñòâà 10 |
∫ab f(x) dx M(b a): |
m(b a) |
Отсюда |
∫ab f(x) dx M: |
m b 1 a |
Но непрерывная функция принимает все свои значения между минимальным и максимальном. Значит, существует такая точка2 [a; b], для которой
1 ∫ b
f( ) = b a a f(x) dx:
Умножив обе части на b a, получаем доказываемое равенство.

9
Лекция 16 февраля 2021 г.
4. Дифференцирование интеграла по верхнему пределу
Рассмотрим функцию f(t), непрерывную на отрезке [a; b].
q q q -
a x b t
|
Ðèñ. 10 |
|
|
|
Положим |
(x) = ∫ax f(t) dt: |
|
||
Найдем ′(x). Имеем |
|
|
||
|
′(x) = lim |
(x + ∆x) (x) |
: |
|
|
|
|||
|
∆x!0 |
∆x |
|
|
Вычислим выражение в числителе |
|
|
||
(x + ∆x) (x) = ∫ax+∆x f(t) dt |
∫ax f(t) dt |
|
||
= ∫ax f(t) dt + ∫xx+∆x f(t) dt |
∫ax f(t) d = ∫xx+∆x f(t) dt: |
|||
По теореме о среднем найдется такая точка 2 [x; x + ∆x], äëÿ
которой ∫ x+∆x
f(t) dt = f( )∆x:
x
Таким образом,
′(x) = lim |
f( )∆x |
= |
lim f( ): |
|
|||
∆x!0 |
∆x |
∆x!0 |
|
Из непрерывности функции f(t) вытекает, что |
|||
lim |
f( ) = f(x): |
||
∆x!0 |
|
|
|
Следовательно, ′(x) = f(x). |
|
|
|
Тем самым доказана следующая теорема.
Теорема 3 (о дифференцировании интеграла по верхнему пределу). Если функция f(t) непрерывна на отрезке [a; b], òî
(∫ x )′
f(t) dt = f(x):
a
Иными словами, мы доказали, что (x) является первообразной для f(x). Отсюда вытекает, что у каждой непрерывной функции есть первообразная.
10
5. Основная формула интегрального исчисления. Формула Ньютона Лейбница
Пусть функция f(t) непрерывна на отрезке [a; b]. Мы выяснили, что ∫ x
(x) = f(t) dt
a
является первообразной для f(x). Пусть F (x) какая-то другая первообразная f(x). Тогда они могут отличаться только на посто-
янную. Тем самым |
∫ x |
|
f(t) dt = F (x) + C
a
äëÿ âñåõ x 2 [a; b]. Подставив в это равенство x = a, получаем
0 = F (a) + C:
Следовательно, C = ∫ Fx (a). Итак, мы получили равенство f(t) dt = F (x) F (a):
a
Подставим x = b
∫ b
f(t) dt = F (b) F (a):
a
Эта формула называется формулой Ньютона Лейбница и является основной формулой интегрального исчисления. Часто ее записывают в следующем виде
|
|
|
|
|
|
b |
|
|
ab f(t) dt = F (t) a: |
||||
|
|
∫ |
|
|
|
|
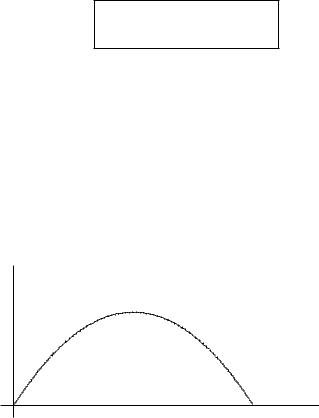
Пример 1. |
|
|
|
|
|
|
0 |
sin t dt = |
|
|
= cos |
|
|
cos t 0 |
( cos 0) = 1 + 1 = 2: |
|||||
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
y 6 |
|
|
|
|
|
|
|
|
|
|
|
||
|
y = sin t |
|
|
|
|
|
0 |
|
t |
Ðèñ. 11
