

В бесконечно малом объеме dV=dlds при наличии электромагнитной волны, движущейся только в одном направлении (прямой, либо обратной), запасена некоторая энергия, плотность которой в пределах бесконечно малого объема постоянна и равна:
W / W Э/ W М/ |
2W Э/ E 2 E |
|
H |
|
EH |
1 |
EH |
|
|
||||||||
|
|
|||||||
|
|
|
|
|
v |
|||
Энергия, запасенная в объеме dV, равна:
dW W / dV EH dl ds EH v dt ds EH ds dt v v

Так как электромагнитная волна движется вдоль оси z со скоростью v, то в том же направлении перемещается и связанная с ней энергия. Мощность потока электромагнитной энергии, проходящей сквозь площадку ds, определяется
соотношением: |
dW |
EH ds |
|
|
|
|
dt |
|
а мощность потока электромагнитной энергии, отнесенная к единице поверхности, обозначается через S , и равна:
dW dt S EH ds
dt S EH ds
Мощность потока электромагнитной энергии через единицу поверхности может рассматриваться как вектор, направленный в сторону движения электромагнитной волны, вместе с которой перемещается и связанная с ней энергия. Этот вектор называется вектором Умова-Пойнтинга, и его направление связано с направлением векторов напряженности электрического и магнитного поля с помощью их
векторного произведения: |
|
|
|
|
S E H

В прямой электромагнитной волне напряженность электрического и магнитного поля одного знака (Ex>0, Hy>0 или Ex<0, Hy<0) вектор скорости направлен вдоль оси z (Vz>0), и вектор Пойнтинга направлен в туже сторону. В обратной электромагнитной волне напряженность электрического и магнитного поля разного знака (Ex>0, Hy<0 или Ex<0, Hy>0) вектор скорости направлен против оси z (Vz<0), и вектор Пойнтинга также направлен против оси z
X E
|
|
|
S |
|
Z |
|
||
|
v |
Y
H
v
X
|
|
|
|
|
S |
Z |
|
|
|
||
Y |
|
|
|
H |
|||
E |
|||
|
|
прямая волна |
обратная волна |
Вектор Пойнтинга определяет мощность потока электромагнитной энергии сквозь единицу поверхности, перпендикулярной направлению движению волны, и совпадает с ним по направлению.
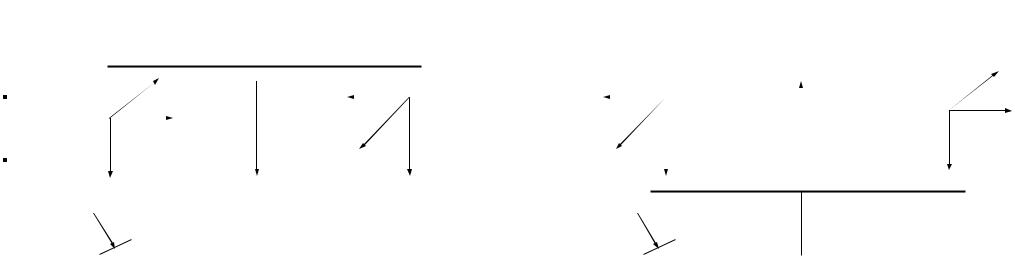
Рассмотрим в качестве примера переходные процессы при заряде и разряде плоского конденсатора
При заряде конденсатора вектор Пойнтинга направлен внутрь конденсатора, и энергия запасается в его электрическом поле, а при разряде – наоборот, конденсатор отдает энергию.
|
+ + + + + + + + + + |
+ + + + + + + + + + |
|
|
|
+ + + + + + + + + + |
+ + + + + + + + + + |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
|
|
|
|
|
H |
|
|
|
|
|
|
|
||||
+ |
|
|
|
|
S |
|
S |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
S |
||||||
_ |
|
S |
JСМ H |
|
|
|
E |
JСМ |
|
||||||
|
|
E |
|
|
|
E |
H |
|
|
E |
|
||||
|
|
|
|
|
|
|
|
|
|
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ |
|
|
|||
|
_ _ _ _ _ _ _ _ _ _ |
_ _ _ _ _ _ _ _ _ _ |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Направление вектора плотности тока смещения совпадает с направлением приращения вектора смещения или вектора напряженности электрического поля:
|
|
|
|
|
|
|
dD |
|
dE |
||
J см |
|||||
dt |
dt |
||||
|
|
|

Случай прямой синусоидальной электромагнитной волны.
Запишем выражения для напряженности электрического и магнитного поля прямой волны в произвольной точке при синусоидальном законе их изменения.
E / x Em sin( t ) |
H / y |
|
E m sin( t ) H m sin( t ) |
|
|||
|
|
|
|
Замена аргумента (ωt+ ) на принятый для бегущих волн аргумент (z-vt) осуществляется введением коэффициента « »:
ωt + = (z – vt).
Записанное соотношение справедливо для любого момента времени. При t=0 получаем = z. Тогда из того же соотношения можем записать:
ωt = – vt, |
откуда |
|
|
|
v
|
|
|
|
|
z |
|
/ |
Em |
|
sin (t |
z |
||
Ex/ Em |
sin( t |
z) Em |
sin (t |
) |
H y |
|
|
) |
|||||
|
v |
||||||||||||
|
|
||||||||||||
|
|
v |
|
v |
|
|
|
|
|
|
|||
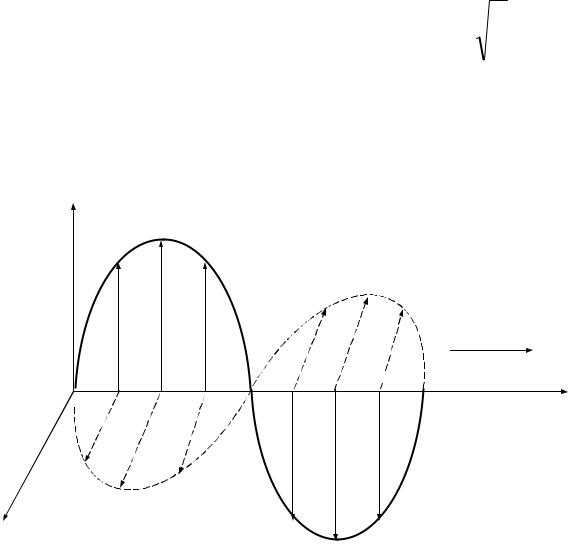
Бегущие волны записаны в обычной форме, из которой видно, что вдоль оси z они также распределены по синусоидальному закону. Картина распределения векторов напряженности электрического и магнитного поля для момента времени t=0,5T представлена на рисунке
x Ex
v
z
y
Hy
В прямой синусоидальной плоско поляризованной электромагнитной волне векторы E и H перпендикулярны друг другу в любой точке пространства, имеют одинаковую начальную фазу и
распространяются без затухания вдоль оси z.

Длина электромагнитной волны в диэлектрике.
Приращение координаты, на котором аргумент волны изменяется на 2 , называется длиной волны ( ). Из соотношения =2 получим:
2 2 v 2 v v2 f f
vT v f
Так как скорость распространения электромагнитной волны в диэлектрике зависит только от его диэлектрических и магнитных свойств и не зависит от частоты передаваемого сигнала, то длина волны в диэлектрике обратно пропорциональна частоте сигнала. Длина электромагнитных волн в воздухе в зависимости от частоты (таблица 11–1) определяется из соотношения:
|
v |
|
c |
|
3 108 |
|
f |
f |
f |
||||
|
|
|
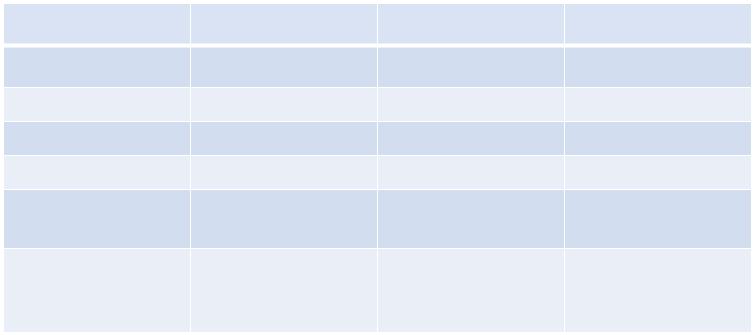
Длина волны в воздухе для различных частот
Частота |
Длина волны |
Диапазон |
Примечание |
|
|
f |
|
|
|
105 |
гц =100 кГц |
3000 м |
Длинные волны |
|
106 |
гц =1 МГц |
300 м |
Средние волны |
|
107 |
гц =10 МГц |
30 м |
Короткие волны |
|
108 |
гц =100 МГц |
3 м |
УКВ; FM; |
ТВ - метровый |
|
|
|
компьютер |
диапазон |
109 |
гц =1000 МГц |
0,3 м |
Мобильная связь |
ТВ - |
|
|
|
|
дециметровый |
|
|
|
|
диапазон |
