
Метод._MathCAD_Prime
.pdf
4 |
x4 18x2 6 0; |
12 |
x4 18x2 6 0; |
|
x3 0,1x2 0, 4x 12 0. |
|
x3 0, 2x2 0,5x 1 0. |
5 |
3x4 8x3 6x2 10 0; |
13 |
x4 x3 2x2 3x 3 0; |
|
x3 3x2 12x 3 0. |
|
x3 3x2 6x 5 0. |
6 |
2x4 x2 10 0; |
14 |
2x4 x2 10 0; |
|
x3 0, 2x2 0, 4x 1, 4 0. |
|
x3 0,1x2 0, 4x 2 0. |
7 |
x4 4x3 8x2 17 0; |
15 |
3x4 4x3 12x2 1 0; |
|
x3 0, 2x2 0,5x 1, 4 0. |
|
x3 0, 2x2 0, 5x 0,8 0. |
8 |
x4 x3 2x2 3x 3 0; |
16 |
3x4 8x3 18x2 2 0; |
|
x3 4x 6 0. |
|
x3 0,1x2 0, 4x 1, 2 0. |
51

Лабораторная работа 4. Решение систем уравнений
Цель: познакомиться с различными способами решения систем уравнений в системе MathCad Prime.
1. Решение систем линейных уравнений матричным методом
Матричный метод. Система линейных уравнений в матричной форме имеет вид Ax B Где, A – матрица коэффициентов системы линейных уравнений; B – вектор свободных членов; x – вектор решения. Решение получают по формуле: x A 1 B , Где, A 1 – обратная матрица. Решение существует, если определитель матрицы A 0 .
Упражнение Решить систему линейных алгебраических уравнений:
x 2 y 3z 7x 3y 2z 5x y z 3
Порядок выполнения:
1. |
Введите матрицу , состоящую из коэффициентов |
|||
2. |
Найти определитель матрицы |
. Если определитель отличен от |
||
нуля, то решение существует. |
|
|
||
3. |
Введите вектор |
– вектор |
свободных |
членов уравнений, |
стоящих справа от знака равно. |
|
|
||
4. |
Запишите формулу расчета корней системы |
· , наберите = |
||
иполучите решение системы уравнений.
5.Сделайте проверку полученного результата, для этого наберите
·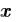 . Если решение найдено верно, то результат совпадет с вектором
. Если решение найдено верно, то результат совпадет с вектором
.
52

Вид документа Mathcad Prime:
2. Решение систем линейных уравнений с помощью функции 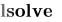
Для решения системы линейных уравнений в Mathcad Prime используют функцию 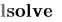
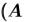
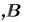
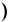 , Где,
, Где, 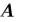 – матрица коэффициентов системы линейных уравнений; – вектор свободных членов.
– матрица коэффициентов системы линейных уравнений; – вектор свободных членов.
В функции 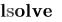 запрограммирован численный метод LU-разложения, основанный на алгоритме последовательных исключений Гаусса. Он состоит в преобразовании матрицы A линейной системы к треугольному виду, т. е. к форме, когда все элементы ниже главной диагонали матрицы являются нулевыми. Точнее, исходная система
запрограммирован численный метод LU-разложения, основанный на алгоритме последовательных исключений Гаусса. Он состоит в преобразовании матрицы A линейной системы к треугольному виду, т. е. к форме, когда все элементы ниже главной диагонали матрицы являются нулевыми. Точнее, исходная система 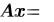 заменяется эквивалентной системой с другой матрицей
заменяется эквивалентной системой с другой матрицей 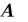 и другим вектором правых частей
и другим вектором правых частей 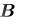 , но имеющей то же решение, что и исходная система.
, но имеющей то же решение, что и исходная система.
Упражнение Решить систему линейных уравнений:
x 2 y 3z 12x 3y z 2x 2 y 5z 3
Порядок выполнения:
1.Введите матрицу , состоящую из коэффициентов 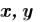
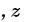

2.Введите вектор B – вектор свободных членов уравнений, стоящих справа от знака равно.
53

3. Для решения системы линейных уравнений введите функцию
Вид документа Mathcad Prime:
3.Решение систем нелинейных уравнений с помощью «блока решений»
Если необходимо решить систему нелинейных уравнений, то рассмотренные выше методы не годятся. Для этих целей в Mathcad Prime имеются функции 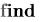 и , применение которых предусмотрено только в «блоке решений».
и , применение которых предусмотрено только в «блоке решений».
Блок решения – это контейнер, который может содержать любые другие области. Блоки решения используются для решения систем линейных, нелинейных или дифференциальных уравнений, а также для решения задач оптимизации. Блоки решения осуществляют поиск решения методом итераций, начиная с заданных значений начальных приближений. Часто найденное решение является аппроксимацией фактического решения, приемлемость которой определяется значениями допуска сходимости и допуска ограничения .
Каждый блок решения может иметь только одну функцию решения. Однако если в конце одного блока решения определить какую-либо функцию, например 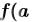
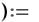 ( ), то ее можно будет использовать в другом блоке решения. Первый блок решения при этом называется параметризованным блоком решения.
( ), то ее можно будет использовать в другом блоке решения. Первый блок решения при этом называется параметризованным блоком решения.
Кроме функции в блоке решений необходимо задать начальные приближения, а также начальные или граничные условия. Начальное приближение к корням системы уравнений можно определить графическим способом. Если ожидается, что решение будет
комплексным, |
необходимо |
задать |
комплексные |
начальные |
приближения. Если задача решается для |
переменных, |
блок решения |
||
54
должен содержать уравнений. Допускается матричное представление как при решении с матричными переменными.
Функции  (
(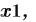
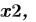 ),
), 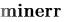 (
(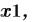
 ) возвращают значения
) возвращают значения 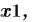
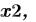 удовлетворяющие уравнениям и неравенствам, заданным в блоке решения. Аргументы
удовлетворяющие уравнениям и неравенствам, заданным в блоке решения. Аргументы 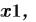
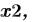
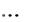 являются скалярами или переменными-массивами, имеющимися в системе уравнений. Эти функции могут использоваться только в блоке решения!
являются скалярами или переменными-массивами, имеющимися в системе уравнений. Эти функции могут использоваться только в блоке решения!
Функция 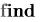 выбирает подходящий метод из группы имеющихся методов в зависимости от того, является задача линейной или нелинейной, а также исходя из других параметров.
выбирает подходящий метод из группы имеющихся методов в зависимости от того, является задача линейной или нелинейной, а также исходя из других параметров.
Функция отличается от функций 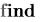 тем, что если выбранный алгоритм не сходится, то возвращается ответ, найденный на последней допустимой итерации, даже если он не удовлетворяет критерию
тем, что если выбранный алгоритм не сходится, то возвращается ответ, найденный на последней допустимой итерации, даже если он не удовлетворяет критерию
сходимости. Если алгоритм сходится, то функция |
возвращает те |
|
же результаты, что и |
. |
|
Если имеется только одна неизвестная переменная, решением будет скаляр. В противном случае решением будет вектор, в котором первый элемент – переменная 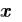 , второй –
, второй –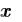 и т. д.
и т. д.
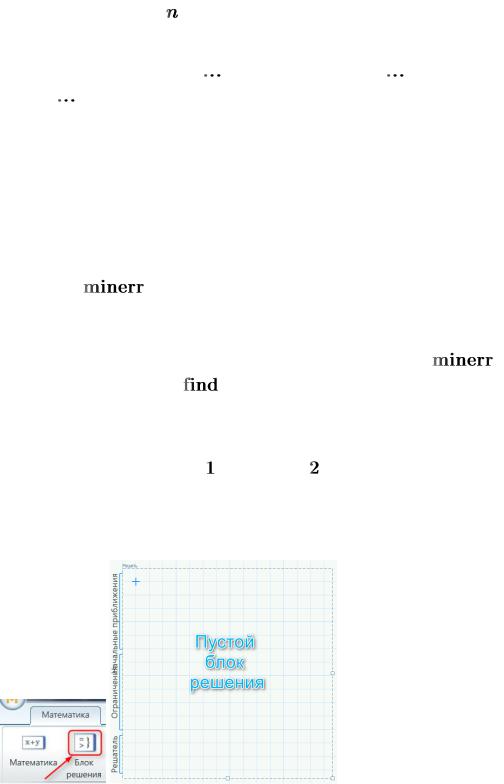
Вставка в документ блока решения:
Примечание: При вводе уравнения, вместо обычного знака равенства = необходимо использовать логический оператор сравнения (жирный знак равенства  ).
).
55
|
|
|
|
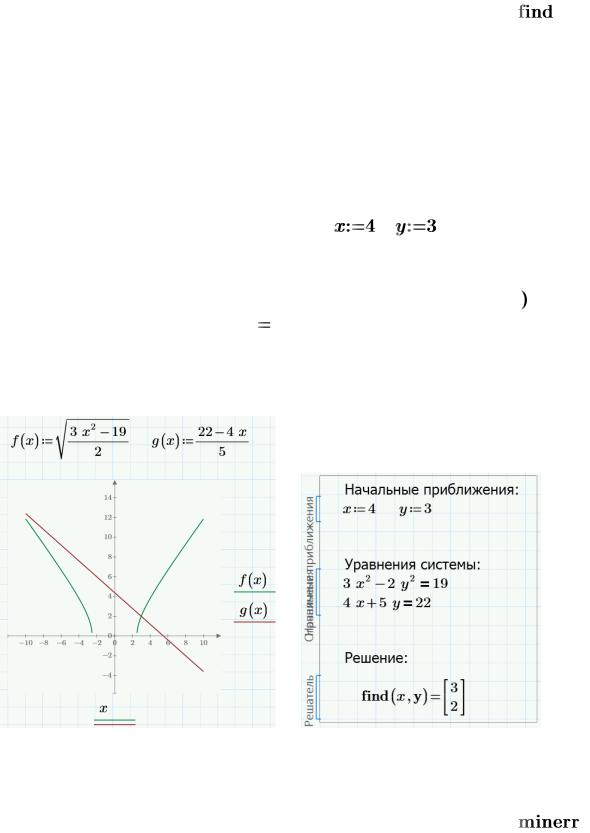
Упражнение 1 |
|
Решить систему нелинейных уравнений с помощью функции |
: |
||||
|
2 |
2 y |
2 |
19 |
|
3x |
|
|
|
||
4x 5y 22 |
|
||||
Порядок выполнения:
1.Постройте графики для обеих уравнений.
2.Вставьте блок решения.
3. Введите начальные приближения |
и |
. |
4.Введите заданные уравнения, используя логический оператор сравнения  из вкладки Математика/Операторы/Сравнение.
из вкладки Математика/Операторы/Сравнение.
5.Для получения решения, введите функцию 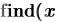
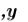 , и затем
, и затем
обычный знак равенства .
Вид документа Mathcad Prime:
Упражнение 2 |
|
Решить систему нелинейных уравнений с помощью функции |
: |
xy2 1 0
y ex 0
56

Порядок выполнения:
1.Вставьте блок решения.
2.Введите начальные приближения 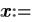 и
и 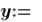 .
.
3.Введите заданные уравнения, используя логический оператор сравнения  из вкладки Математика/Операторы/Сравнение.
из вкладки Математика/Операторы/Сравнение.
4.Для получения решения, введите функцию 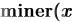
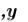 , и затем
, и затем
обычный знак равенства .
Вид документа Mathcad Prime:
|
|
|
Индивидуальные задания |
1. |
Решить |
систему |
линейных уравнений матричным способом |
|
x : A1 B (Табл.1). |
||
2. |
Решить систему линейных уравнений с помощью встроенной |
||
|
функции |
(Табл.2). |
|
3. |
Решить систему нелинейных уравнений с помощью встроенных |
||
|
функции |
и |
(Табл.3). |
57

Таблица 1
|
№ |
Система уравнений |
№ |
Система уравнений |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1 |
4x1 |
x2 |
4x3 |
138 |
2 |
3x1 |
4x2 |
2x3 |
162 |
||||||
|
|
|
|
4x2 |
6x3 |
225 |
|
|
5x2 |
3x3 |
200 |
|||||
|
|
2x1 |
|
x1 |
||||||||||||
|
|
|
2x2 |
x3 80 |
|
|
2x3 |
110 |
|
|||||||
|
|
x1 |
|
x2 |
|
|||||||||||
|
3 |
2x1 |
6x2 |
x3 |
470 |
4 |
2x1 |
2x2 |
5x3 |
345 |
||||||
|
|
|
3x2 |
2x3 |
305 |
|
|
|
3x2 |
6x3 |
520 |
|||||
|
|
x1 |
|
3x1 |
||||||||||||
|
|
|
x3 109 |
|
|
|
|
|
3x2 |
4x3 |
455 |
|||||
|
|
x2 |
|
|
|
4x1 |
||||||||||
|
5 |
2x1 |
x2 |
3x3 |
110 |
6 |
2x1 |
3x2 |
4x3 |
655 |
||||||
|
|
|
|
7x2 |
6x3 |
315 |
|
|
|
x2 |
4x3 |
588 |
||||
|
|
8x1 |
|
3x1 |
||||||||||||
|
|
|
|
4x2 2x3 |
115 |
|
|
2x2 2x3 |
360 |
|||||||
|
|
3x1 |
|
x1 |
||||||||||||
|
7 |
2x1 |
6x2 |
x3 |
225 |
8 |
3x1 |
4x2 |
180 |
|||||||
|
|
|
3x2 |
2x3 |
225 |
|
|
|
5x2 |
x3 |
255 |
|||||
|
|
x1 |
|
4x1 |
||||||||||||
|
|
|
x3 120 |
|
|
|
|
|
3x2 |
3x3 |
200 |
|||||
|
|
x2 |
|
|
|
2x1 |
||||||||||
|
9 |
x1 2x2 |
x3 200 |
10 |
2x1 |
2x2 |
125 |
|||||||||
|
|
|
2x2 |
4x3 |
315 |
|
|
|
4x2 |
x3 |
305 |
|||||
|
|
x1 |
|
5x1 |
||||||||||||
|
|
|
|
5x2 |
3x3 |
544 |
|
|
x2 2x3 120 |
|||||||
|
|
3x1 |
|
x1 |
||||||||||||
|
11 |
3x1 |
5x2 |
5x3 |
185 |
12 |
x2 2x3 |
140 |
|
|||||||
|
|
|
|
x2 |
2x3 |
185 |
|
|
|
x2 |
x3 175 |
|||||
|
|
7x1 |
|
2x1 |
||||||||||||
|
|
|
6x2 |
80 |
|
|
|
|
|
7x2 x3 290 |
||||||
|
|
x1 |
|
|
|
3x1 |
||||||||||
|
13 |
3x1 |
x3 |
115 |
|
14 |
3x1 |
3x2 |
x3 |
135 |
||||||
|
|
|
|
7x3 150 |
|
|
|
2x3 |
155 |
|||||||
|
|
2x2 |
|
6x2 |
||||||||||||
|
|
|
3x2 |
2x3 |
143 |
|
|
9x2 |
2x3 |
230 |
||||||
|
|
x1 |
|
x1 |
||||||||||||
|
15 |
3x1 |
5x2 |
6x3 |
640 |
16 |
2x1 |
2x2 |
x3 |
50 |
||||||
|
|
|
|
4x2 |
x3 |
380 |
|
|
|
5x2 |
3x3 |
140 |
||||
|
|
2x1 |
|
3x1 |
||||||||||||
|
|
|
|
x2 |
3x3 |
175 |
|
|
|
7x2 |
x3 |
125 |
||||
|
|
3x1 |
|
2x1 |
||||||||||||
58

Таблица 2
№ |
|
Система уравнений |
№ |
Система уравнений |
||||||||||
1 |
2x1 x2 2x3 3x4 8 |
2 |
2x1 x2 5x3 x4 4 |
|||||||||||
|
|
|
3x3 6 |
|
|
|
|
3x2 6x4 7 |
||||||
|
3x1 |
|
|
|
x1 |
|||||||||
|
|
|
x2 3x4 4 |
|
|
|
|
x3 2x4 2 |
||||||
|
2x1 |
|
|
2x2 |
||||||||||
|
x 2x x 2x 4 |
|
x 4x 7x 6x 2 |
|||||||||||
|
|
1 |
2 |
3 |
4 |
|
|
1 |
|
2 |
|
3 |
|
4 |
3 |
x1 2x2 3x3 4x4 22 |
4 |
x1 2x2 3x3 4x4 26 |
|||||||||||
|
|
|
3x2 x3 2x4 17 |
|
|
|
3x2 4x3 x4 34 |
|||||||
|
2x1 |
|
2x1 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
4x2 x3 2x4 26 |
||||
|
x1 x2 x3 x4 8 |
|
|
3x1 |
||||||||||
|
x 2x 3x 7 |
|
|
4x x 2x 3x 26 |
||||||||||
|
|
1 |
3 |
4 |
|
|
|
|
1 |
2 |
|
3 |
|
4 |
5 |
9x1 10x2 7x3 x4 23 |
6 |
2x1 8x2 3x3 2x4 18 |
|||||||||||
|
|
|
x3 5x4 37 |
|
|
|
2x2 3x3 2x4 28 |
|||||||
|
7x1 |
|
|
x1 |
||||||||||
|
|
|
2x3 x4 22 |
|
|
|
x3 x4 10 |
|||||||
|
5x1 |
|
|
x2 |
||||||||||
|
4x x 2x 3x 26 |
|
11x x 2x 21 |
|||||||||||
|
|
1 |
2 |
3 |
4 |
|
|
|
|
2 |
3 |
|
4 |
|
7 |
6x1 |
x2 10x3 |
x4 158 |
8 |
2x1 |
x2 |
4x3 |
x4 66 |
||||||
|
|
|
x2 10x3 |
7x4 |
128 |
|
|
|
6x2 |
x4 |
63 |
|||
|
2x1 |
|
2x1 |
|||||||||||
|
|
|
2x2 |
2x3 |
x4 7 |
|
|
|
3x2 |
6x3 |
5x4 146 |
|||
|
3x1 |
|
8x1 |
|||||||||||
|
x 12x 2x x 17 |
|
2x 7x 6x x 80 |
|||||||||||
|
|
1 |
2 |
3 |
4 |
|
|
|
1 |
|
2 |
|
3 |
4 |
9 |
x1 2x2 6x3 x4 88 |
10 |
2x1 3x3 2x4 16 |
|||||||||||
|
|
|
2x3 |
3x4 |
88 |
|
|
|
|
x2 13x3 |
4x4 213 |
|||
|
5x1 |
|
|
2x1 |
||||||||||
|
|
|
3x2 |
7x3 |
2x4 |
181 |
|
|
|
x2 2x3 |
x4 72 |
|||
|
7x1 |
|
3x1 |
|||||||||||
|
3x |
7x |
5x |
2x |
99 |
|
x 12x |
5x |
4 |
159 |
||||
|
|
1 |
2 |
3 |
4 |
|
|
1 |
|
|
3 |
|
|
|
11 |
x1 2x2 8x4 7 |
|
12 |
7x1 7x2 7x3 2x4 5 |
||||||||||
|
|
|
|
|
|
|
|
|
|
4x2 5x3 8x4 60 |
||||
|
x1 4x2 7x3 6x4 8 |
|
3x1 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
2x2 2x3 x4 27 |
||||
|
x1 x2 5x3 x4 10 |
|
2x1 |
|||||||||||
|
2x x 2x 7 |
|
|
2x 2x x 1 |
||||||||||
|
|
1 |
2 |
4 |
|
|
|
|
1 |
|
3 |
4 |
|
|
13 |
2x1 |
2x2 |
6x3 |
x4 15 |
14 |
6x1 |
9x2 |
5x3 |
x4 124 |
|||||
|
|
|
2x3 x4 18 |
|
|
|
|
5x3 x4 54 |
||||||
|
x2 |
|
|
7x2 |
||||||||||
|
|
|
3x2 x3 5x4 37 |
|
|
|
5x2 2x3 4x4 83 |
|||||||
|
4x1 |
|
5x1 |
|||||||||||
|
3x 5x x x 30 |
|
3x 9x x 6x 45 |
|||||||||||
|
|
1 |
2 |
3 |
4 |
|
|
|
1 |
|
2 |
3 |
|
4 |
15 |
4x1 |
5x2 |
7x3 |
5x4 |
165 |
16 |
x1 2x2 |
2x3 |
4x4 30 |
|||||
|
|
|
x2 3x3 x4 15 |
|
|
|
2x2 3x3 4x4 10 |
|||||||
|
2x1 |
|
x1 |
|||||||||||
|
|
|
4x3 |
x4 194 |
|
|
|
x3 x4 3 |
|
|||||
|
9x1 |
|
|
x2 |
|
|||||||||
|
x x 2x 3x 19 |
|
x 5x x x 10 |
|||||||||||
|
|
1 |
2 |
3 |
4 |
|
|
1 |
|
2 |
|
3 |
|
4 |
59

Таблица 3
№ |
Система уравнений |
№ |
Система уравнений |
|||||||||||||
1 |
|
|
0, 4) |
|
x |
2 |
2 |
2x2 5 y2 3 |
||||||||
|
tg(xy |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
2 y2 1 |
|
|
9 y 3 |
|||||||||||
|
0, 6x2 |
|
|
5x |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
sin(x |
y) 1, 6x 0 |
4 |
3x |
|
4 y |
|
4 |
||||||||
|
|
|
2 |
|
2 |
|
||||||||||
|
x2 y2 1 |
|
|
|
|
|
3x 4 y 2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
1) y 1, 2 |
6 |
5x |
|
2 y |
|
4 |
||||||||
|
sin(x |
|
|
2 |
|
2 |
|
|||||||||
|
2x cos( y) 2 |
|
|
|
2x 7 y 1 |
|||||||||||
7 |
|
1) y 0,5 |
8 |
4x 5 y 3 |
||||||||||||
|
cos(x |
|
|
2 |
|
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x cos( y) 3 |
|
|
|
|
5x 3y 1 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
10 |
5x |
|
6 y |
|
3 |
|
cos(x) y 1,5 |
|
|
|
2 |
|
2 |
|
||||||||
|
2x sin( y 0,5) 1 |
|
7x 3y 1 |
|||||||||||||
11 |
|
|
0,1) |
|
x |
2 |
12 |
3x2 5y2 3 |
||||||||
|
tg(xy |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
2 y 2 |
||||
|
x2 y2 1 |
|
|
|
|
|
5x |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
sin(x y) 1, 2x 0, 2 |
14 |
7x2 6 y2 3 |
|||||||||||||
|
x2 y2 1 |
|
|
|
|
|
5x 3y 2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
x |
2 |
|
|
|
|
16 |
5x2 6 y2 3 |
|||||
|
tg(xy) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2 y2 1 |
|
|
|
2 y 2 |
||||||||||
|
0,8x2 |
|
|
|
3x |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
60
