
Частина2
.pdf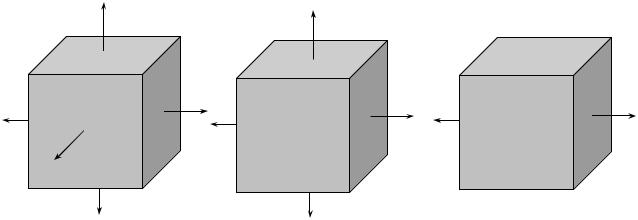
Матриця напружень (3.1) носить назву тензора напружень, а елементи цієї матриці називаються компонентами тензора напружень.
Тензор напружень {G} позбавлений фізичного змісту. Фізичний зміст мають лише ком-
поненти тензора напружень.
На основі закону парності дотичних напружень (див. 2.2), дотичні напруження, що виникають на двох взаємно перпендикулярних площинках, рівні і протилежні за напрямом. Тобто
txy |
= |
t yx |
; |
txz |
= |
tzx |
; |
t yz |
= |
tzy |
(3.2) |
|
|
|
|
|
|
|
|
|
|
|
|
Компоненти тензора напружень залежать від напрямків вибраних координатних осей. Тензор напружень володіє рядом властивостей. Зокрема певні комбінації компонент тензора напружень є інваріантними відносно вибору системи координат(на залежать від вибору системи координат). Тому інваріанти є основними характеристиками напруженого стану в точці.
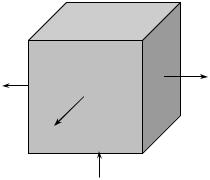
Виділений з тіла елемент можна зорієнтувати таким чином, що по його площинках виникатимуть тільки нормальні напруження, а дотичні будуть рівні нулеві (рис. 3.1, в). Площинки, на яких дотичні напруження рівні нулеві– головні площинки. Нормальні напруження, що діють на головних площинках – головні напруження.
В кожній точці тіла можна вказати три взаємно перпендикулярні площинки, на яких діють головні напруження .
В залежності від того, скільки головних напружень відмінні від нуля, відрізняють об’ємний (рис. 3.2, а), плоский (рис. 3.2, б) і лінійний (рис. 3.2, в) напружений стан.
s3 |
|
s3 |
|
|
|
|
|
|
s1 |
s1 |
s1 |
|
|
s2
а) |
б) |
в) |
рис. 3.2
На рис. 3.2 показані лише розтягуючі головні напруження, однак вони можуть бути як розтягуючими так і стискуючими.
При аналізі плоского (лінійного) напруженого стану виникають два типи задач:
1)при відомих головних напруженнях, визначити нормальні і дотичні напруження, що виникають на заданій площинці (пряма задача);
2)при відомих нормальних і дотичних напруженнях, що виникають на двох довільних взаємно перпендикулярних площинках, знайти положення головних площинок і визначити величину головних напружень (обернена задача).
-21 -
3.2. Аналіз плоского напруженого стану.
1. Пряма задача.
Плоским напруженим станом називають такий, коли три із компонент напружень рівні нулеві.
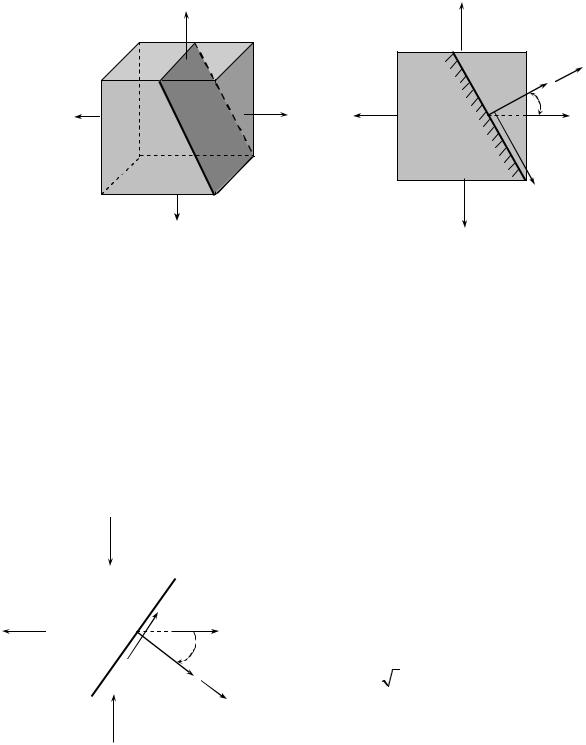
Нехай задано елементарний кубик, грані якого є головними площинками. На цих площинках діють головні напруженняs1 , s2 (рис.3.3. а) Потрібно визначити напруження на заштри-
хованій |
s2 |
s3 |
|
|
na |
|
sa |
s1 |
a |
s1
ta
а) |
б) |
рис. 3.3
площинці, перпендикулярній до фасадної грані і довільно нахиленій до бокових граней, зовнішня нормаль до якої утворює з напрямком напруженняs1 кут a , який вважатимемо додатнім при відкладанні проти ходу стрілки годинника (рис.3.3, б).
Напруження на таких площинках знаходяться за формулами:
|
|
|
2 |
|
|
2 |
|
ü |
|
sa = s1 cos a +s2 sin |
|
a |
(3.3) |
||||||
|
ï |
||||||||
ta = |
s |
1 |
-s |
2 |
sin 2a |
|
|
ý |
|
|
|
|
|
ï |
|
||||
|
|
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
þ |
|
|
Приклад 3.1. |
На гранях виділеного з тіла елемента діють головні напруження, що показані на |
||||||||||||||||||
|
|
s3 =10 МПа |
|
рис. 3.4. Визначити нормальні і дотичні напруження |
|||||||||||||||
|
|
|
на площинці, нахиленій до горизонтальної осі під вка- |
||||||||||||||||
|
|
|
|
|
заним на рисунку кутом a = 300 . |
|
|||||||||||||
|
|
|
|
|
Із |
формул (3.3), врахувавши, |
що напруження |
||||||||||||
|
|
|
|
|
|||||||||||||||
s1 |
|
|
s1 = 40 МПа |
s3 = -10 МПа (стиск) і кут a = -300 |
(за ходом стріл- |
||||||||||||||
|
|
ки годинника) отримуємо: |
|
|
|
|
|||||||||||||
|
|
ta |
a |
|
sa = s1 cos2 a +s3 sin2 a = |
|
|||||||||||||
|
|
|
|
|
|
æ |
|
|
|
ö |
2 |
|
æ 1 ö2 |
|
|||||
|
|
sa |
|
|
|
|
3 |
+ (-10) |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
n |
= |
40 ×ç |
|
|
|
÷ |
|
|
×ç |
|
÷ = 27,5 МПа ; |
|||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
a |
|
|
ç |
|
2 |
÷ |
|
|
|
è 2 ø |
|
||||
|
|
|
|
|
|
|
è |
|
ø |
|
|
|
|
||||||
|
|
s3 |
|
tа |
= |
|
s1 |
-s3 |
|
sin 2a = |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
рис. 3.4
- 22 -
= 40 - (-10) sin 2(-300 )= -21,5 МПа. |
|
|
|
|||
2 |
|
|
|
|
|
|
Тобто, на нахиленій площинці виникає розтягуюче напруження sa = 27,5 МПа і дотичне |
||||||
напруження, що оббігає елемент проти ходу стрілки годинника (знак “-“) ta = -21,5 МПа . |
||||||
2. Обернена задача. |
|
|
|
|
|
|
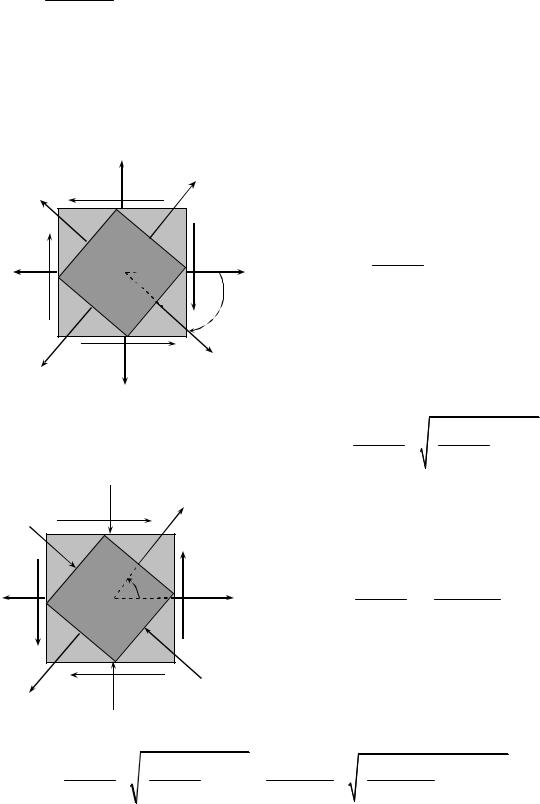
При плоскому напруженому стані задані нормальні і дотичні напруження на двох взаємно |
||||||
перпендикулярних площинках з нормалями, що паралельні до осейx і y (рис. 3.5). Потрібно |
||||||
s y |
|
|
знайти положення головних площинок і величину го- |
|||
|
|
ловних напружень. |
|
|
||
txy |
s |
2 |
Положення |
головної площинки по |
відношенню |
|
|
|
до площинки з |
напруженнямs x задається |
кутом a , |
||
|
txy |
|||||
|
що знаходиться з формули |
|
||||
|
|
sx |
tg 2a = - |
2t yx |
|
(3.4) |
|
|
|
|
|
||
|
|
|
s x -s y |
|
|
|
|
|
a |
При чому, коли s x |
> s y ,то знайдений кут a – це |
||
|
|
s1 |
кут між напрямками s x |
і s1 , коли s x < s y |
- між на- |
|
|
|
прямками s x і s2 . |
|
|
||
|
|
|
|
|
||
|
|
|
Величина головних напружень знаходиться з ви- |
|||
|
|
рис. 3.5 |
|
|
|
|
разу : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
s |
1 |
ü |
s |
x |
+s |
y |
æ s |
x |
-s |
y |
ö2 |
+t yx2 |
(3.5) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
ý = |
|
2 |
± ç |
|
2 |
|
÷ |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
s2 þ |
|
|
|
è |
|
|
|
|
ø |
|
|
|
|||||
|
|
|
s y |
= 10 МПа |
|
|
|
|
|
|
Приклад 3.2. |
Для |
елемента, |
що показаний |
||||||||||||||
|
|
|
|
txy |
s1 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
на рис. 3.6, знайти положення головних площинок |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
і визначити головні напруження. |
|
||||||||||||||||
|
|
|
|
a |
sx |
= 50 МПа |
|
|
Положення головних площинок : |
|||||||||||||||||||
|
|
|
|
tg 2a = - |
|
2t yx |
|
= - |
2 (-30) |
|
= 1 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
s x -s y |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
txy |
= 30 МПа |
|
|
|
|
50 - (-10) |
|
|
|
||||||||||||||
|
|
|
|
|
2a = 450 , |
a = 22030' |
(проти |
ходу |
стрілки годин- |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
s2 |
|
|
ника). |
Оскільки |
s x > s y , |
то |
знайдений кут a це |
||||||||||||||
|
|
|
|
|
|
|
|
|
кут між напрямками s x і s1 . |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
рис. 3.6 |
|
|
|
|
|
|
Величина головних напружень: |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
s1 ü |
s x |
+s y |
± |
æ s x |
-s y |
ö2 |
2 |
= |
50 |
+ (-10) |
± |
æ 50 - (-10) ö2 |
|
|
|
|
|
2 |
= 20 |
± 42, 3; |
||||||||
ý = |
|
2 |
ç |
2 |
÷ |
|
+t yx |
|
2 |
|
|
ç |
|
|
2 |
|
÷ + (-30) |
|
||||||||||
s2 þ |
|
|
è |
ø |
|
|
|
|
|
|
|
è |
|
|
|
ø |
|
|
|
|
|
|
|
|
||||
s1 = 20 + 42,3 = 62,3 МПа |
( розтяг) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
s 2 = 20 - 42, 3 = -22, 3 МПа ( стиск ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Головні напруження і їх напрямки показані на рис. 3.6. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
- 23 - |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3.3. Головні напруження та деформації при об’ємному напруженому стані.
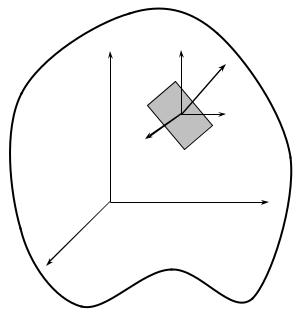
Якщо відомий тензор напружень в системі координат0xyz, то напруження на довільній площадці, нормаль якої складає з осями системи координат кутиa , b , g , визначаються за формулами
X n |
= s x cosa +txy cos b +txz cosg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Yn |
=txy cosa + s y cos b +t yz cosg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Zn |
= txz cosa +tzy cos b +s z cosg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На окремих площадках , які визначаються кутами a , b , g можуть виникати тільки но- |
|||||||||||||||||
рмальні напруження. Ці площадки є головними. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
Для об’ємного напруженого стану величини |
||||||||||||
|
z |
Zn |
головних напружень визначаються із кубічного рів- |
||||||||||||||
|
няння |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
r |
|
|
s |
3 |
- I1 s |
2 |
+ I2 s - I3 |
= 0 , |
|
(3.6) |
|||||
|
|
n |
|
|
|
|
|
||||||||||
|
|
|
де I1 , I2 , |
|
I3 – |
|
інваріанти |
напруженого |
стану, що |
||||||||
|
|
Yn |
знаходяться із виразів |
|
|
|
|
|
|
||||||||
|
|
X n |
I1 = s x +s y +s z |
|
|
|
|
|
|
ü |
|||||||
|
|
|
I2 = s xs y +s ys z +s zsx -txy2 |
-tyz2 -tzx2 |
|
ï |
|||||||||||
|
|
|
|
ý (3.7) |
|||||||||||||
|
|
y |
I |
3 |
= s s s |
z |
+ 2t t t |
-s t 2 |
-s t 2 |
-s t 2 ï |
|||||||
|
|
|
x y |
|
|
|
xy yz zx |
|
x |
yz |
y zx |
z |
xy þ |
||||
|
|
|
|
|
Величини (3.7) є інваріантними відносно ви- |
||||||||||||
x |
|
|
бору системи координат . |
|
|
|
|
|
|||||||||
|
|
|
|
При дії головних напруженьs1 , s2 , s3 в |
|||||||||||||
|
|
|
|
|
|||||||||||||
|
|
рис. 3.7 |
виділеному з тіла безмежно малому елементі вини- |
||||||||||||||
|
|
катимуть |
|
в напрямку |
цих |
напружень деформації |
|||||||||||
e1 , e2 , e3 , які визначаються із узагальненого закону Гука:
e1 =
e2 =
e3 =
1 |
|
és |
|
- m s |
|
|
|
+s |
|
|
ù |
ü |
|
||
|
|
|
|
|
|
|
|
|
|||||||
E ë |
1 |
|
( |
|
2 |
|
3 )û ï |
|
|||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
|
és |
|
- m (s |
|
+s |
|
)ù |
ï |
(3.8) |
||||||
|
|
2 |
3 |
1 |
ý |
||||||||||
E |
ë |
|
|
|
|
|
|
|
û |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
|
1 |
|
és |
3 |
- m |
( |
s |
1 |
+s |
|
|
ù |
ï |
|
||
|
|
|
|
|
|
||||||||||
E |
ë |
|
|
|
|
2 )ûï |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
þ |
|
|
3.4. Розрахунок на міцність при складному напруженому стані. Теорії міцності.
Найважливішою задачею інженерного розрахунку елементу конструкції є оцінка міцності цього елементу при відомому напруженому стані.
Для лінійного напруженого стану(розтяг або стиск) це задача розв’язується просто, оскільки в цьому випадку значення граничних напружень можна визначити експериментально. За величиною граничних напружень знаходять допустимі їх значення, ввівши коефіцієнт запа-
су міцності і формулюють умову міцності для лінійного напруженого стану таким чином
- 24 -
(3.9)
Значно складнішим є випадок об’ємного чи плоского напруженого стану, коли в точках є два або три головні напруження s1 , s2 , s3 . Досліди показують, що для того самого матері-
алу граничний стан може наступати при різних граничних значеннях напружень s1 , s2 , s3 , в
залежності від співвідношень між ними. Тому експериментально встановити граничні значення головних напружень практично неможливо не тільки тому, що такі експерименти важко здійснити , але й тому, що їх треба було б проводити надзвичайно багато (при різних співвідношеннях s1 , s2 , s3 ). У зв’язку з цим, для розв’язування поставленої задачі пішли іншим шля-
хом – шляхом допущення про переважаючий вплив на міцність матеріалу того чи іншого фактору. Вважають, що руйнування матеріалу при довільному напруженому стані відбувається тільки тоді, коли величина цього фактору досягне граничного значення. Граничне значення фактору, що визначає міцність, визначають з експериментів, зокрема при лінійному напруженому стані (при розтягу або стиску), який легко здійснити.
Розрахунок на міцність при складному напруженому стані здійснюється виходячи із теорій (гіпотез) міцності, коли ця міцність оцінюється на основі механічних характеристик матеріалу, що одержані при його випробуванні при лінійному напруженому стані(при розтягу чи стиску).
Теорії міцності розділяють на три групи:
а) теорія міцності для крихкого руйнування; б) теорія міцності для пластичного руйнування;
в) теорія міцності для матеріалів, що по різному опираються розтягу і стиску (теорія міцності Мора).
Крихке руйнування – це руйнування матеріалів з дуже малими пластичними деформаціями. Це руйнування відбувається шляхом відриву однієї частини тіла від другої. Характеристи-
кою міцності матеріалу в цьому випадку є величина нормального напруження відривуs .
відр
Наближено приймають sвідр = s м , де s м – границя міцності матеріалу.
Пластичне руйнування – руйнування пов’язане з великими пластичними деформаціями, що виникають внаслідок зміщення (зсуву) одних частин тіла відносно інших. Деформація зсуву пов’язана з дотичними напруженнями t . Тому опір матеріалу пластичному руйнуванню характеризується величиною напруження tт , що відповідає границі текучості матеріалу.
На прикладі розтягу встановлено, що
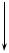 s3
s3
s2
|
tт |
= |
sт |
. |
|
|
|
|
|||
|
|
2 |
|
|
|
|
Серед теорій міцності для крихкого руйнування прак- |
||||
|
тичне застосування знаходять : |
|
|||
|
1) |
теорія найбільших нормальних напружень(I |
теорія |
||
s1 |
|
міцності); |
|
||
2) |
теорія найбільших лінійних деформацій(II |
теорія |
|||
міцності).
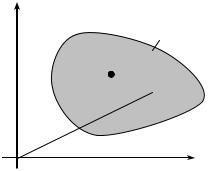
Згідно з теорією найбільших нормальних напружень переважаючий вплив на міцність при об’ємному стані з -на пруженнями s1 ³ s2 ³ s3 (рис.3.8) має величина найбільшого
нормального напруження s1 . Вважається, що міцність пропадає тоді, коли
рис. 3.8 |
s1 = s гр |
- 25 -

де sгр = s м – границя міцності матеріалу при одновісному напруженому стані. |
|
Умова міцності має вигляд |
|
sеквI = s1 £ [s ] |
(3.9) |
де sевкI – еквівалентне (розрахункове) напруження за першою теорією міцності.
Згідно з теорією міцності найбільших лінійних деформаційвважається, що порушення міцності об’ємному напруженому стані, зображеному на рис.3.7, наступає тоді, коли найбільша лінійна деформація emax = e1 досягає свого граничного значення, що знаходиться при розтягу або стиску зразка.
emax = e1 = eгр
Підставивши в останній вираз величину e1 із (3.8) і врахувавши, що при лінійному напруженому стані
eгр = s гр = s м
ЕЕ
умову руйнування можна записати у вигляді
|
1 |
és |
- m |
( |
s |
2 |
+ s |
ù = |
s |
м |
. |
|
|
|
|
||||||||
|
Е |
ë 1 |
|
|
|
3 )û |
Е |
||||
|
|
|
|
|
|
|
|
||||
Тоді умова міцності за даною теорією має вигляд |
|
|
|
||||||||
sеквII = s1 - m (s2 |
+ s3 ) £ [s ] |
|
(3.10) |
||||||||
Серед теорій міцності для пластичного руйнування на практиці використовуються:
1.Теорія найбільших дотичних напружень (III теорія міцності).
2.Теорія питомої потенціальної енергії зміни форми (IV теорія міцності).
Згідно з теорією найбільших дотичних напружень вважається, що пластичне руйнування в випадку об’ємного напруженого стану(рис.3.8) настає тоді, коли найбільше дотичне напруження досягає граничного значення tгр , що визначається при лінійному напруженому стані.
tmax = s1 -s3 = tгр
2
Врахувавши, що при пластичному руйнуванні в випадку одновісного напруженого ста-
ну tгр |
= |
sт |
і ввівши коефіцієнт запасу, дістаємо умову міцності за цією теорією |
|
|
|
|||
|
2 |
sеквIII = s1 -s3 £ [s ] |
|
|
|
|
|
(3.11) |
|
Згідно з теорією питомої потенціальної енергії зміни форми тілапластичне руйнуван-
ня при об’ємному напруженому стані настає тоді, коли питома потенціальна енергія зміни форми досягає свого граничного значення Uфгр , що визначається при лінійному напруженому стані, тобто
|
Uф = Uфгр . |
|
|
Підставивши в останнє співвідношення вирази для Uф |
і Uфгр , |
і ввівши коефіцієнт запа- |
|
су, отримаємо умову міцності за цією теорією |
£ [s ] |
|
|
|
|
|
|
sеквIV = s12 +s22 + s32 -s1s2 -s2s3 -s3s1 |
(3.12) |
||
Дану теорію називають теорією міцності Губера-Мізеса.
Теорія міцності Мора використовується для оцінки міцності тих матеріалів при об’ємному напруженому стані (рис.3.7), в яких границі текучості чи міцності при розтягу і стиску різні, тобто
sт, р ¹ sт,с ; s м, р ¹ s м,с .
- 26 -
Умова міцності за цією теорією має вигляд |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
sевкV = s1 - |
[s ]р |
s3 £ [s ] |
(3.13) |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
[s ]с |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
р |
|
де : |
ìs |
|
|
|
|
|
|
|
|
|
|
|||
|
т, р |
- |
для |
пластичних |
матеріалів; |
|
||||||||
|
ï |
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||||
[s ] |
ï Кт |
|
|
|
|
|
|
|
||||||
= í |
|
|
s м, р |
|
|
|
|
|
|
|||||
р |
ï |
|
|
- для крихких |
матеріалів; |
|
||||||||
|
|
|
|
|||||||||||
|
ï |
|
|
|
К м |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
î |
|
|
|
|
|
|
|
|
|
||||
|
ìs |
т,с |
- |
для |
пластичних |
матеріалів; |
|
|||||||
|
ï |
|
|
|
||||||||||
|
|
|
|
|
||||||||||
[s ] |
ï |
|
Кт |
|
|
|
|
|
|
|
||||
= í |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
ï s м,c |
- |
для |
крихких матеріалів; |
|
|||||||||
|
ï |
|
Км |
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||
|
î |
|
|
|
|
|
|
|
|
|||||
Експериментально встановлено, що перша і друга теорія має ряд недоліків і дає неточні результати. Тому для практичних розрахунків найчастіше використовують четверту або третю теорію міцності для матеріалів, що однаково опираються розтягу і стискові, і теорію міцності Мора – для крихких матеріалів.
Приклад 3.3 Використавши III теорію міцності перевірити міцність елементу при двох на-
|
пружених станах: |
||
1) |
s1 = 100 МПа , |
s 2 |
= 20 МПа , s3 = -80 МПа |
2) |
s1 = 200 МПа , |
s2 |
=100 МПа , s3 = 50 МПа , якщо [s ] = 160 МПа. |
В випадку першого напруженого стану
sеквIII = s1 - s3 = 100 - (-80) =180 МПа > [s ]
Міцність не забезпечена. У другому випадку
s еквIII = 200 - 50 = 150 МПа < [s ]
Умова міцності виконується.
IV. Геометричні характеристики поперечних перерізів.
Основним елементом конструкції, що розглядається в опорі матеріалів є стержні, які працюють на розтяг, стиск, кручення чи згин. Опір стержня зовнішнім силам залежить не тільки від матеріалу стержня, але і від розмірів та форми поперечного перерізу, що враховується за допомогою геометричних характеристик перерізу.
Розглянемо основні геометричні характеристики поперечних перерізів стержня. y
4.1. Статичні моменти, моменти інерції.
A
|
zC |
C |
|
dA |
|
Статичними моментами перерізу (рис.4.1) віднос- |
|||||
|
|
|
|
|
|
|
но осей y, z називають величини |
|
|||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
S y = òz dA; |
Sz = ò y dA |
(4.1) |
|
z |
|
|
|
|
|
|
|
|||
|
|
yC |
|
|
|
|
|||||
|
r |
|
|
|
y |
|
A |
A |
|
||
|
|
|
|
|
|
Якщо відомо положення центра перерізу(коорди- |
|||||
O |
|
|
|
|
|
|
z |
нати центра С - zc , |
yc ), то вирази (4.1) можна записати у |
||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
вигляді |
|
|
|||
|
|
|
|
|
|
|
|
|
|||
рис. 4.1
- 27 -
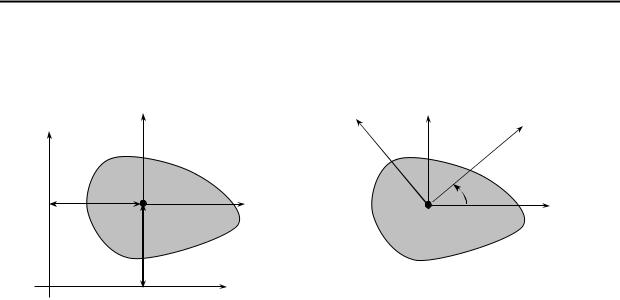
S y = zc × A; Sz = yc × A |
(4.2) |
Із співвідношення (4.2) випливають формули для визначення положення центра перерізу в координатній системі O y z
z |
|
= |
Sy |
; |
y = |
S |
z |
c |
|
|
|
||||
|
|
A |
|
c |
A |
||
|
|
|
|
|
|||
(4.3)
Положення центра складного перерізу, який можна розкласти на такі прості частини, для кожної з яких відома площа і положення центра, визначають із формул :
z |
|
åSy(i) |
; y |
|
åSz(i ) |
|
|
= |
i |
= |
i |
(4.4) |
|||
åFi |
åFi |
||||||
c |
|
c |
|
|
|||
|
|
i |
|
|
i |
|
Осі, що проходять через центр перерізу, називають центральними осями. Статичні моменти відносно центральних осей дорівнюють нулеві.
Моменти інерції бувають (рис.4.1) а) осьові (відносно осей y і z)
I y |
= ò z2 dA, |
Iz = ò y2 dA |
(4.5) |
|
A |
A |
|
б) полярний (відносно полюса “O”) |
|
|
|
I p |
= ò r2 dA ; |
|
(4.6) |
в) відцентровий |
A |
|
|
= ò y z dA |
|
|
|
I yz |
|
(4.7) |
|
|
A |
|
|
Між осьовими і полярними моментами існує очевидна залежність |
|
||
I p |
= Iz + I y |
|
(4.8) |
Осьові і полярний момент інерції завжди додатні, а відцентровий може набувати додатних і від’ємних значень. При певному положенні осейY, Z він може бути рівний нулеві. Осі, відносно яких відцентровий момент дорівнює нулеві, називаються головними осями.
4.2.Моменти інерції при паралельному переносі і повороті осей. Головні центральні осі. Головні моменти інерції.
Якщо відома величина моментів інерції перерізу відносно центральних осейy , z |
c |
c |
(рис.4.2а), то моменти інерції відносно довільних осей y, z, що паралельні до заданих центральних осей, знаходиться за формулами
y |
y |
y1 |
y |
|
C |
|
C |
z 1 |
|
|
|
|
||
b |
C |
|
|
a |
|
z C |
C |
|
zC |
|
a |
|
|
|
|
z |
|
|
|
|
a) |
б) |
|
|
|
|
рис.4.2. |
|
|
- 28 -

I z = I zc |
+ a2 A ü |
|
I y = I yc |
ï |
|
+ b2 A ý |
(4.9) |
|
|
ï |
|
I yz = I yc zc + abAþ |
|
|
де a, b – координати центра перерізу (точки С) відносно осей y, z ; А – площа перерізу. Фор-
мули (4.9) носять назву формули для моментів інерції при паралельному переносі осей.
Якщо відомі моменти інерції відносно довільних центральних осейy, z (рис.4.2б), то моменти інерції відносно центральних осей y1 , z1 , що повернуті відносно перших осей на кут a (додатним кутом вважається кут повороту проти ходу стрілки годинника), визначаються за
формулами |
|
|
|
|
|
|
|
|
|
|
|
|
|
ü |
|
I z |
= I z cos2 a + I y sin 2 a - I yz sin 2a ï |
|
|||||
1 |
|
|
|
|
|
ï |
|
I y |
= I z sin 2 a + I y cos2 a + I yz sin 2aý |
(4.10) |
|||||
1 |
|
|
I z - I y |
|
ï |
|
|
|
|
|
|
|
|||
|
I y z = |
|
|
sin 2a + I yz cos 2a |
ï |
|
|
|
|
2 |
|
||||
|
1 |
1 |
|
|
þ |
|
|
|
|
|
|
|
|
||
Формули (4.10) – це формули для моментів інерції при повороті осей. |
|
||||||
Склавши перший і другий вираз системи (4.10), отримуємо |
|
||||||
|
|
I z |
+ I y = I z + I y |
|
(4.11) |
||
|
|
1 |
1 |
|
|
|
|
Тобто при повороті осей сума осьових моментів не змінюється.
Головними центральними осями перерізу називаються такі центральні , осівідносно яких відцентровий момент інерції I yz дорівнює нулеві.
Якщо переріз має безліч осей симетрії (круг, кільце), то будь-які центральні осі є головними центральними.
Якщо переріз має дві осі симетрії (прямокутник, двотавр), то ці осі симетрії є головними центральними осями.
Якщо переріз має одну вісь симетрії(рівнобедрений трикутник, швелер), то ця вісь симетрії і перпендикулярна до неї вісь, що проходить через центр перерізу, є головними центральними осями.
Якщо переріз не має жодної осі симетрії, то положення головних центральних осей відносно довільних центральних осей zc , yc задається кутом a , який знаходиться із співвідношення
tg 2a = - |
2I yc zc |
(4.12) |
||
I zc |
- I yc |
|||
|
|
|||
(додатній кутa відкладається проти ходу стрілки годинника).
Головними моментами інерції перерізу називаються осьові моменти інерції, визначені відносно його головних центральних осей. Серед інших осьових моментів інерції відносно довільних центральних осей перерізу головні моменти інерції набувають екстремального(max, min) значення. Ці головні моменти визначаються з виразу
I |
max |
ü |
|
I z |
+ I y |
c |
|
æ I z |
c |
- I y |
ö |
2 |
|
|
|
|
|
|
c |
|
ç |
|
c ÷ |
2 |
|
||||
|
|
ý |
= |
|
|
|
± |
ç |
|
|
|
÷ |
+ I yc zc |
(4.13) |
|
|
|
2 |
|
|
|
2 |
|||||||
Imin þ |
|
|
|
|
è |
|
|
ø |
|
|
||||
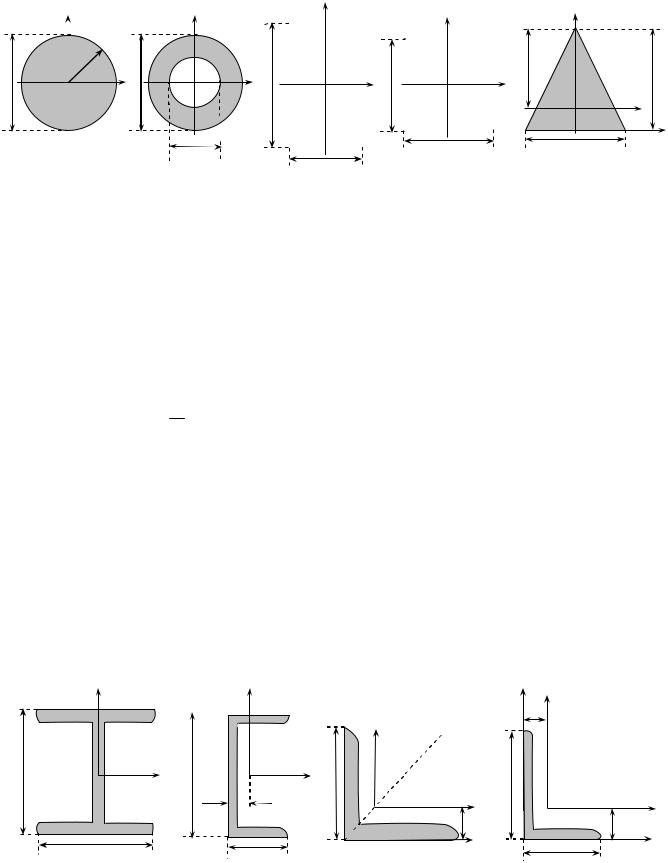
4.3 Моменти інерції деяких простих перерізів.
Обчислимо моменти інерції для деяких простих перерізів, що часто зустрічаються при інженерних розрахунках. Ці моменти обчислюються шляхом інтегрування, за формулами (4.5), (4.6). Такими перерізами є круг, кільце, прямокутник, квадрат, трикутник.
- 29 -
|
y |
|
y |
|
|
y |
|
y |
|
|
y |
|
|
|
|
|
|
|
|
|
2 |
||||
|
|
|
|
|
|
|
||||||
|
r |
|
D |
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
3 |
|||
d |
|
|
|
h |
|
|
a |
|
|
h |
||
C |
z |
C |
z |
C |
z |
C |
z |
|
||||
|
|
|
|
C |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
z z1 |
|
|
|
d |
|
|
|
|
|
a |
|
|
b |
|
|
|
|
|
b |
|
||||||
|
|
|
|
|
|
|
|
|
|
|||
|
a) |
|
б ) |
|
|
|
|
|
|
д) |
||
|
|
|
|
в) |
|
г) |
|
|
||||
рис. 4.3.
1. Круг з радіусом r, діаметром d (рис.4.3 а)
I z |
= I y = |
p r 4 |
= |
p d 4 |
» 0,05d 4 |
; I p |
= |
p r 4 |
= |
p d 4 |
» 0,1d 4 . |
|
|
|
|
||||||||
|
4 |
64 |
|
|
2 |
32 |
|
||||
2. Кругове кільце з внутрішнім діаметром d і зовнішнім діаметром D (рис.4.3 б)
I z = I y = |
p D 4 |
(1 -a 4 )» 0,05 D 4 (1 -a 4 ) |
; I p = |
p D |
4 |
(1 -a 4 )» 0,1D 4 (1 -a 4 ), |
|
|
|
||||
64 |
|
32 |
|
|
||
де позначено a = d .
|
|
|
|
|
D |
|
|
|
|
|
|
|
3. |
Прямокутний переріз з розмірами b, h (рис.4.3 в) |
|||||||||||
|
I z = |
b h3 |
; |
I y = |
h b3 |
; |
|
I p = I z + I y . |
||||
|
12 |
|
12 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||
4. |
Квадратний переріз із стороною а (рис.4.3 г) |
|||||||||||
|
I z = |
I y = |
a 4 |
; I p = 2I z |
= |
|
a |
4 |
. |
|||
|
12 |
6 |
||||||||||
|
|
|
|
|
|
|
|
|
||||
5. Переріз у вигляді рівнобедреного (рівностороннього) трикутника з розмірами b, h (рис.4.3 д)
|
|
b h |
|
|
h b3 |
|
b h3 |
||
I z |
= |
3 |
; I y |
= |
|
; I z = |
|
. |
|
36 |
48 |
12 |
|||||||
|
|
|
|
1 |
|
||||
|
|
|
|
|
|
|
|
||
6. Переріз у вигляді прокатних профілів – двотавра (рис.4.4 а), швелера (рис.4.4 б), рівнобічного кутника (рис.4.4 в), нерівнобічного кутника (рис.4.4 г).
y |
y |
|
y1 |
z |
y |
|
|
|
|||
|
|
y |
|
0 |
|
|
|
|
|
|
|
z |
z |
|
|
|
|
h |
h |
|
B |
|
|
|
b |
z |
|
z |
|
|
z0 |
|
|
||
|
z0 |
|
|
y0 |
|
|
|
|
|
||
b |
b |
z |
|
|
z1 |
|
1 |
|
|
b |
|
a) |
б) |
в) |
|
|
|
|
|
г) |
рис.4.4.
- 30 -
