
Частина3
.pdf
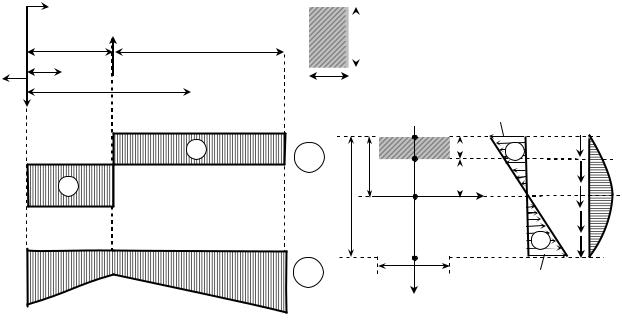
·Згинальний момент M(x) у довільному перерізі чисельно дорівнює алгебраїчній сумі моментів або лівих або правих сил відносно центра перерізу. Додатнім вважаються моменти від тих сил, що викликають розтяг нижніх волокон балки.
y
RA F M RB
x
B
A
x
M (x) Q(x) |
M |
RB |
Q(x) > 0 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
M (x) > 0 |
|||
RA |
|
|
||||
M (x) |
|
|
|
|||
|
|
|
|
|||
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q(x)
рис. 7.5.
Правила знаків для Q(x) і M(x) схематично показані на рис.7.5.
На основі аналітичних виразів дляQ(x) і M(x) будують графіки зміни цих величин по довжині балки, які називаються епюрами Q(x) і M(x).
7.3. Епюри Q(x) і M(x) для деяких найпростіших випадків навантаження балки.
y
|
|
|
|
RA |
= |
F b |
|
|
|
|
|
|
RB |
= |
F a |
||
|
|
|
|
|
|
|
|
l |
|||||||||
H A |
l |
F |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
A |
|
|
|
C |
|
|
|
B |
x |
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
a |
|
b |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
F b |
|
|
|
x |
|
|
x |
|
|
|||||||
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|||||
|
l |
|
|
F |
- |
|
|
|
F a |
|
Q |
||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
M
F a b
l
рис. 7.6.
1. Проста |
балка, |
навантажена |
|||||||
|
зосередженою силою F (рис.7.6). |
||||||||
Опорні реакції : |
|
|
|
|
|
|
|
||
åX = 0 ; H A = 0 ; |
|
|
Fa |
|
|
||||
å |
M A = 0; RB |
×l - F ×a = 0; RB |
= |
; |
|||||
|
|
||||||||
|
|
|
|
|
l |
||||
åM B = 0; RA |
×l - F ×b = 0; RA |
= |
Fb |
. |
|||||
|
|||||||||
|
|
|
|
|
|
l |
|||
Перевірка åY = 0, RA + RB - P = 0
виконується.
Вирази для Q(x) і M(x) по ділянках балки:
|
|
AC (0 £ x £ a) |
|
|
|
|
|
|
|||
Q(x) = RA |
= |
Fb |
; M (x) = RA |
× x = |
Fb |
× x ; |
|||||
|
|
|
|
||||||||
|
|
l |
|
|
|
l |
|
||||
|
|
BC (0 £ x £ b) |
|
|
|
|
|
|
|||
Q(x) = -R |
= - |
Fa |
; M (x) = R |
B |
× x = |
Fa |
× x. |
||||
|
|
||||||||||
B |
|
|
|
l |
|
|
l |
|
|||
|
|
|
|
|
|
|
|
||||
- 41 -
y
RA = M
l M
A |
C |
|
a |
b |
|
x |
x |
|
M |
+ |
|
l |
||
|
||
|
M b |
|
|
l |
|
|
M |
|
|
M a |
|
|
l |
|
|
рис. 7.7. |
RB = M l
B
 x
x
Q
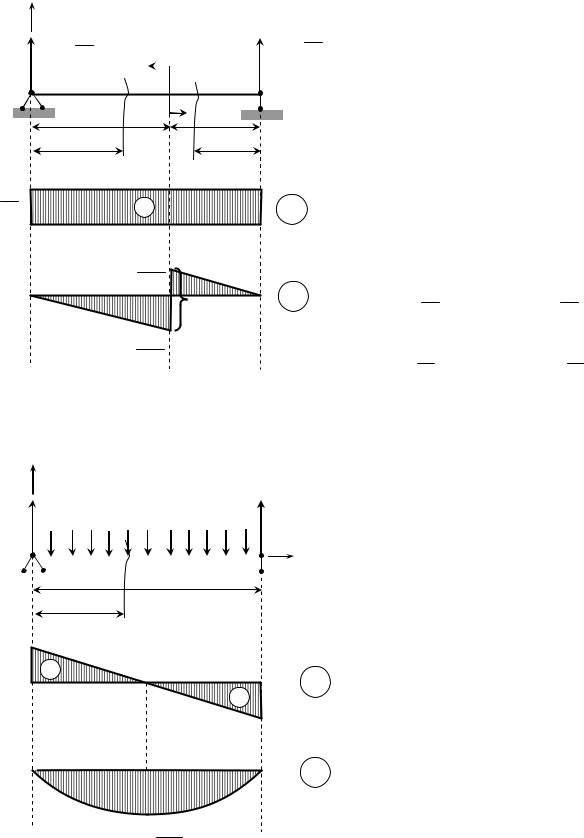
Епюри Q(x) і M(x), що побудовані за цими виразами, показані на рис.7.6. Зауважимо, що на епюрі Q(x) в точці С, де прикладена сила F є стрибок на величину сили. Додатні значення на епюрі M(x) відкладаються з тієї сторони, де є розтягнуті волокна, тобто знизу. Знак на епюріM(x) можна не ставити.
2.Проста балка, навантажена парою сил з
моментом М (рис.7.7). Опорні реакції в цьому випадку
RA |
= |
M |
; |
RB |
= - |
M |
(вниз); |
|
l |
||||||
|
|
l |
|
|
|
||
Вирази для Q(x)
AC
M Q(x) = RA = M ; l
BC
Q(x) = RB = M ; l
і M(x):
(0 £ x £ a)
M (x) = RA × x = M × x; l
(0 £ x £ b)
M (x) = -RB × x = - M × x. l
Епюри Q(x) і M(x) показані на рис.7.7. Зауважимо, що на епюрі M(x) у перерізі, в якому прикладена пара сил з моментом М (точка С), є стрибок на величину моменту цієї пари.
y
|
|
|
RA |
= |
q l |
q |
|
RB |
= |
q l |
||||
|
|
|
|
|||||||||||
|
|
|
|
|
||||||||||
|
|
|
|
|
2 |
|
|
|
|
2 |
||||
|
A |
|
|
|
|
|
|
B |
x |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
q l |
+ |
|
|
|
|
|
|
|
|
|
|
|||
2 |
|
|
|
- |
|
q l |
|
|
Q |
|||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
M
q l 2
8 рис. 7.8.
3.Проста балка під рівномірно
розподіленим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
навантаж |
|||
інтенсивності q (рис.7.8) |
|
ql |
|
|
|
|||||||||||||
Опорні реакції |
RA = RB = |
; H A = 0 . |
|
|||||||||||||||
|
|
|||||||||||||||||
Вирази для Q(x) і M(x): |
|
|
2 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
AB (0 £ x £ l ) |
|
|
|
|
|
|
|
|
||||||||
|
|
Q(x) = RA - qx = |
ql |
- qx ; |
|
|||||||||||||
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
qx2 |
|
|
||
|
M (x) = RA x - qx × |
x |
= |
|
ql |
× x |
- |
|
||||||||||
|
2 |
2 |
2 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Поперечна |
сила Q(x) |
|
|
|
змінюється |
за |
||||||||||||
лінійним законом, а згинальний момент |
|
|||||||||||||||||
M(x) - за законом |
|
|
квадратної параболи. |
|
||||||||||||||
Знаходимо екстремальне значення M(x). З |
|
|||||||||||||||||
умови екстремуму |
dM (x) |
= 0 маємо |
|
|||||||||||||||
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|||
|
ql |
- qx = Q(x) = 0 ; x = |
l |
. |
|
|
|
|
|
|
||||||||
2 |
2 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тобто M(x) досягає екстремального
- 42 -
значення в тій точці, де Q(x)=0, тобто посередині прольоту балки. Це значення дорівнює
M екстр = M (x) |
|
|
= |
ql 2 |
||
x= |
l |
|
. |
|||
8 |
||||||
2 |
|
|
||||
Епюри Q(x) і M(x) для даної балки показані на рис.7.8.
Побудова епюр Q(x) і M(x) для більш складних випадків навантажень балки принципово нічим не відрізняється від розглянутих вище простих випадків.
7.4Диференціальні залежності між згинальним моментом, поперечною силою та інтенсивністю розподіленого навантаження. Правила для перевірки епюр.
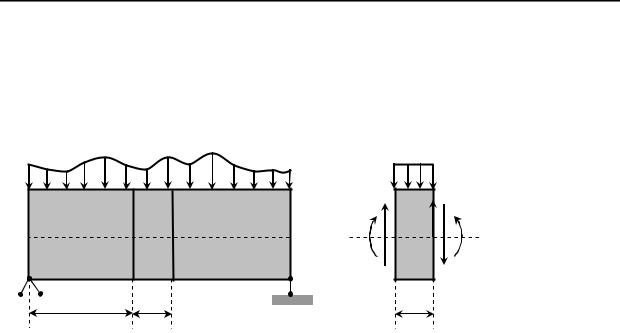
Розглянемо балку, навантажену розподіленим навантаженнямq (рис.7.9). Двома безмежно близькими перерізами виділимо з неї безмежно малий елемент довжиноюdx. Прикладемо до елементу як зовнішні так і внутрішні сили, врахувавши при цьому, що Q(x) і M(x), які діють на правій грані, будуть відрізнятись від значень на лівій грані приростамиdQ і dM.
q
|
x |
d x |
|
|
q |
Q(x) |
y |
M (x) |
M (x)+ d M (x) |
|
O |
|
Q(x)+ d Q(x) |
d x
рис. 7.9.
Зрівнянь рівноваги цього елемента отримаємо:
åY = 0 ; Q(x) - qx - [Q(x) + dQ(x)]= 0
Звідки |
|
|
dQ(x) |
|
|
|
|
|
|
|
|
|
|
|
= -q |
|
|
(7.1) |
|||
|
|
|
|
|
|
|
||||
|
|
|
dx |
|
|
|
|
|||
åM 0 = 0 ; M (x) + Q(x)dx - qdx × |
dx |
- [M (x) + dM (x)]= 0 , |
|
|
||||||
|
|
|
||||||||
|
2 |
|
|
|
|
|
|
|
||
звідки, після нехтування квадратом малої величини (dx)2 : |
|
|
||||||||
|
|
|
dM (x) |
= Q(x) |
|
(7.2) |
||||
|
|
|
|
|
||||||
|
|
|
|
dx |
|
|
|
|
||
Після підстановки значення Q(x) з виразу (7.2) в (7.1), отримаємо |
|
|||||||||
|
|
|
d 2 M (x) |
= -q |
|
(7.3) |
||||
|
|
|
|
dx2 |
|
|||||
|
|
|
|
|
|
|
|
|||
Вирази (7.1) – (7.3) носять |
назву диференціальних залежностей при згині. |
Вони |
||||||||
встановлюють чіткий зв’язок між |
навантаженнямq, |
поперечною |
силою Q(x) та згинальним |
|||||||
моментом M(x). |
|
|
|
|
|
|
|
|
|
|
Ці залежності та деякі |
факти, що були |
встановлені |
в попередньому |
параграфі, |
||||||
дозволяють сформулювати наступні правила для перевірки або побудови епюр:
1.На ділянках балки, де відсутнє розподілене навантаженняq, Q(x) – постійна, а M(x) - лінійна функція.
-43 -

2.На ділянках балки, де прикладено рівномірно розподілене навантаженняq, Q(x) - лінійна функція, а M(x) – парабола.
3.На відрізку ділянки балки, де прикладене q, на якому Q(x)>0, M(x) - зростає, а там де Q(x)<0, M(x) зменшується. В точці, де Q(x)=0, M(x) приймає екстремальне значення.
4.На ділянці балки, де Q(x) º 0 , згинальний момент M(x)=const. Згин балки в цьому випадку називають чистим згином.
5.Якщо в якійсь точці балки прикладена сила, то в цій точці Q(x) має стрибок на величину цієї сили, а на епюрі M(x) буде перелом.
6.Якщо в якійсь точці балки прикладена пара сил з моментом М, то в цій точці M(x) має стрибок на величину момента.
Приклад 7.1 Для балки, зображеної на рис.7.10, скласти вирази для поперечної силиQ(x) та згинального момента M(x), побудувати та перевірити їх епюри.
На місці опор, в точках А і В, прикладаємо реакції RA , RB , спрямувавши їх початково вверх. (горизонтальна реакція в т. А рівна нулеві і на рисунку вона не показана.)
|
|
RA |
|
|
|
q |
RB = 30 kH |
||||
M = 10 kH × м |
|
|
|
|
|
|
|
||||
|
A |
|
C |
|
|
|
|
B |
|||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
||||||
|
|
|
|
|
1 м |
F = 40 kH |
3 м |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
x |
|
|
x |
||||||
|
|
|
|
x |
|
||||||
RA = 10 kH |
30 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
|
|
A |
|
C |
+ |
D |
|
|
B Q |
||
10 |
|
|
|
|
|||||||
|
|
- |
|
|
- |
|
|
||||
|
|
|
|
|
|
|
|
|
|
||
10 |
|
|
|
|
|
|
30 |
|
|||
|
|
|
|
|
|
|
|
|
|
||
M
M max = 22,5kH × м
рис. 7.10.
Рівняння статики:
åM B = 0 ; RA × 4 + M + F × 3 - q ×3 ×1,5 = 0
RA = -10 - 40 × 3 + 20 × 3 ×1,5 = -10 кН . 4
åM A = 0 ; RB × 4 - q ×3 × 2,5 + F ×1 - M = 0
RB = 20 × 3 × 2,5 - 40 ×1 +10 = 30 кН . 4
- 44 -

Величину реакції RA отримали із знаком“-“. Це означає, що початково вибраний напрям реакції вверх є невірним. В дійсності реакція RA =10 кН напрямлена вниз(на схемі балки показано зміну напряму реакції).
Перевірка : åY = 0 ; - RA + F - q ×3 + RB = 0 ; -10 + 40 - 60 + 30 = 0 .
Складаємо вирази для Q(x) і M(x) по ділянках балки AC і BC та обчислюємо значення Q і M в характерних точках.
AC (0 £ x £ 1 м)
Q(x) = -RA = -10 кН ( постійна величина );
M (x) = -RA × x + M = -10x +10 ( лінійна функція ) ; M (0) = 10 кНм ; М (1) = 0
BC (0 £ x £ 3 м)
Q(x) = -RB + qx = -30 + 20x ( лінійна функція ); Q(0) = -30 кН ; Q(3) = 30 кН ;
M (x) = RB × x - qx × x = -30x -10x2 ( парабола ) ; M (0) = 0 ; М (3) = 0 2
Знайдемо екстремальне значення функції М(х):
dM (x) = 0; 30 - 20x = 0; x =1,5 м; M (1,5) = 30 ×1,5 -10 ×1,52 = 22,5кНм. dx
За цими даними побудовані епюриQ(x) і M(x).Ординати епюри M(x) відкладені зі сторони розтягнутих волокон. Це відповідає тому, що додатні значення M(x) відкладені знизу від осі.
Перевірка епюр (за правилами з 7.4):
1.На ділянці АС немає розподіленого навантаженняq, тому на цій ділянціQ(x)=const, і M(x) - лінійна функція.
2.Ділянці ВС є розподілене навантаженняq, тому на цій ділянці Q(x) – лінійна функція, M(x) – парабола.
3.На відрізку CD ділянки ВС Q(x)>0, тому на цьому відрізку M(x) зростає; на відрізку DB Q(x)<0, тому на цьому відрізку М(х) зменшується. В точці D Q(x)=0, тому в цій точці М(х) досягає екстремального значення.
4. В точках А, В, С балки до неї прикладені зосереджені силиR |
=10 кН ; R |
B |
=30 кН ; |
A |
|
|
F =40 кН . Тому в цих точках епюра Q(x) має стрибки на величину цих сил.
5. В точці А балки прикладена пара сил з моментомМ=10 кНм, тому в цій точці епюра М(х) має стрибок на величину моменту.
7.5. Нормальні напруження при чистому і поперечному згині.
При |
згині балки довільним навантаженням у |
поперечних перерізах виникають |
|
поперечна |
сила Q(x) і згинальний момент М(х). Ці |
величини |
є рівнодійними дотичних і |
нормальних напружень, що розподіляються певним |
чином у поперечному перерізі. Закони |
||
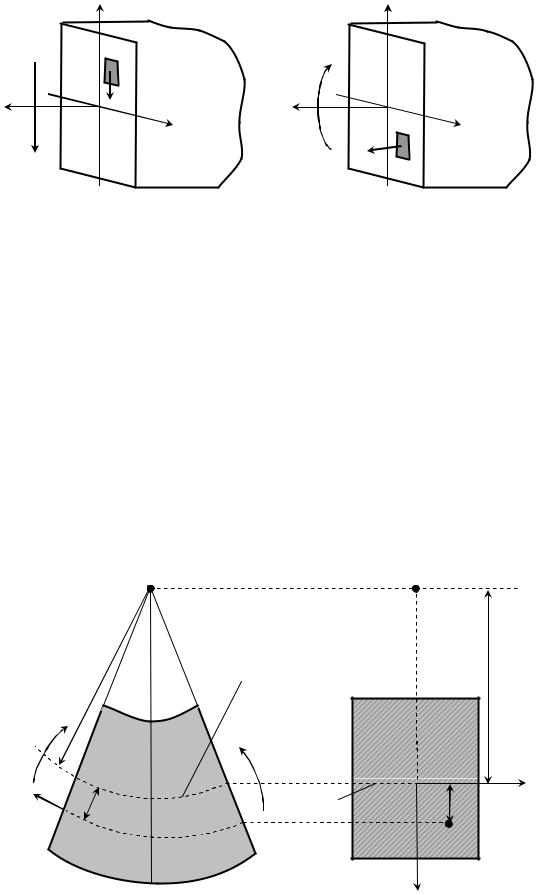
розподілу їх невідомі і тому можна записати лише сумарні(інтегральні) залежності (рис.7.11). |
|||
Q(x) = òt yxdA |
ü |
|
ï |
|
|
A |
ï |
(7.4) |
M (x) = òs ydA |
ý |
|
ï |
|
|
ï |
|
|
A |
þ |
|
Щоб із співвідношень(7.4) визначити нормальне і дотичне напруження, в опорі матеріалів вводять певні допущення (гіпотези), щодо розподілу цих напружень по перерізу.
- 45 -
|
y |
|
|
|
|
y |
|
|
|
||
x |
dA |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
tyx |
z |
|
|
|
z |
|
|
|
|||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
s |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q(x) |
|
|
|
M (x) |
dA |
|
|
|
||
|
|
|
|
|
рис. 7.11. |
|
|
|
|
|
|
Для визначення |
величини |
нормальних напруженьs |
розглядають |
спочатку |
окремий |
||||||
випадок згину – чистий |
|
згин, при |
якому M(x)=M=const і Q(x)=0. В цьому |
випадку |
дотичне |
||||||
напруження t ,що пов’язане з поперечною силою Q(x), відсутнє. |
|
|
|
||||||||
При чистому згині друга з інтегральних залежностей (7.4) набирає вигляду |
|
||||||||||
|
|
|
M = òs y d A |
|
|
|
|
|
(7.5) |
||
A
Закон розподілу нормальних напружень при чистому згині можна встановити, виходячи з експериментального вивчення деформації згину на гумових моделях. Встановлено, що при чистому згині волокна, які лежать на опуклій стороні балки, видовжуються, а ті, що на ввігнутій – стискуються (рис.7.12). Оскільки перехід від перших до других є плавним, то, очевидно, існує шар волокон, при згині не змінює своєї довжини. Цей шар називають нейтральним шаром. Встановлено, що нейтральний шар– це горизонтальний шар, який проходить через центри перерізів. Лінію перетину нейтрального шару з поперечним перерізом
називають нейтральною лінією. Нею є горизонтальна вісь z, що проходить через центр перерізу.
Встановлено також, що при чистому згині виконується гіпотеза плоских перерізів. Виходячи з цієї гіпотези і враховуючи, що при чистому згині виконується закон Гука,
O O
r |
нейт.шар |
r |
M
M
z
s |
y |
нейт. лінія |
y |
|
y
рис. 7.12.
- 46 -
s = E e |
(7.6) |
||
встановлено наступний закон розподілу s в поперечному перерізі |
|
||
s = |
E |
y |
(7.7) |
|
|||
|
r |
|
|
де Е – модуль пружності матеріалу балки; r - радіус кривизни нейтрального шару; y – ордината точки, в якій визначається напруження.
Підставивши вираз (7.7) в співвідношення (7.5) і враховуючи при цьому, що
ò y 2 × dA = I z , де I z – осьовий момент інерції відносно осі z, знаходимо, що
A
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
= |
M |
|
|
|
|
|
|
|
(7.8) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
I z |
|
|
|
|||||||||
Тоді з виразу (7.7) отримаємо формулу для нормальних напружень при чистому згині балки |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
s = |
M × y |
|
|
|
|
|
(7.9) |
|||||||
|
Напруження s вважають |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
I z |
|
|
|
|||||||||||||
балки. |
додатнім у |
розтягнутих і від’ємними |
у стиснутих |
волокнах |
|||||||||||||||||||||||
В симетричному відносноz перерізі максимальні |
за |
абсолютною |
величиною |
||||||||||||||||||||||||
|
|||||||||||||||||||||||||||
напруження виникають у верхніх або нижніх точках перерізу(при |
y = ymax ), що найбільш |
||||||||||||||||||||||||||
віддалені від нейтральної осі z. Якщо позначити |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I z |
=Wz |
|
(7.10) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ymax |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
де Wz |
– осьовий момент опору перерізу відносно осі z, то |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
smax |
= |
M × ymax |
= |
M |
|
|
(7.11) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I z |
|
|
|
Wz |
|
|
|
|||||
|
Якщо переріз балки симетричний відносно горизонтальної, тоосі при визначенні |
||||||||||||||||||||||||||
напружень в крайніх |
точках |
перерізу |
доцільно користуватись |
формулою(7.11). |
Епюра |
||||||||||||||||||||||
|
smin = |
|
smax |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
s1 |
|
1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
- |
|
|
|
|
|
|
|
|
h |
|
M |
|
|
M |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
C |
|
2 z |
|
|
|
|
|
|
- |
|
|
y1 |
|||||||
M |
|
|
|
|
|
M |
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
z |
|
+ |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
+ 2 |
|
|
2 |
y2 |
||||||||
|
smax |
|
|
y |
|
|
|
|
|
|
|
|
|
s2 |
|
y |
|
||||||||||
|
a) |
|
|
|
|
|
|
|
|
|
|
б) |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
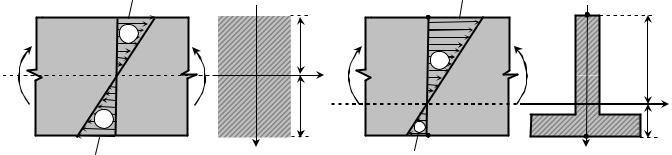
рис. 7.13.
розподілу нормальних напружень s по висоті такого перерізу показана на рис.7.13а.
Якщо переріз балки |
несиметричний |
|
|
відносно горизонтальної центральноїz осі |
||||||||
(рис.7.13б), тоді віддалі крайніх точок від нейтральної осі z є різними. |
||||||||||||
В цьому випадку s = |
M y1 |
; s |
2 |
= |
M y2 |
; |
|
s |
2 |
|
¹ s . |
|
|
|
|||||||||||
|
|
|||||||||||
1 |
I z |
|
|
I z |
|
|
|
1 |
||||
|
|
|
|
|
|
|
|
|
||||
Епюра нормальних напружень для такого перерізу показана на рис.7.13 б.
- 47 -
Для поширених простих перерізів момент опору Wz дорівнює: а) для круглого перерізу з діаметром d
Wz = |
pd 3 |
» 0,1d |
3 |
|
(7.12) |
|||||
32 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||
б) для прямокутного перерізу з шириною b і висотою h |
|
|
||||||||
Wz = |
bh2 |
|
|
|
|
(7.13) |
||||
6 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||
в) для квадратного перерізу із стороною а |
|
|
||||||||
Wz = |
a3 |
|
|
|
|
(7.14) |
||||
6 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
d |
|
||
г) для кільцевого перерізу з зовнішнім діаметром D і внутрішнім d (при |
=a ) |
|||||||||
|
||||||||||
|
|
|
|
|
pD3 |
(1- a4 )= 0,1D3 (1- a4 ) |
D |
|||
|
Wz = |
(7.15) |
||||||||
|
|
|||||||||
32
д) для прокатних профілів (двотавра, швелера, кутника) моменти опору знаходяться із таблиць сортаменту.
Приведені вище формули для нормальних напружень s одержані для випадку чистого згину балки. Якщо має місце поперечний згин, при якому виникають одночасно поперечна сила Q(x) та згинальний моментM(x), що змінюються по довжині балки, то гіпотеза плоских перерізів, яка використовується при одержанні формули(7.9) для нормальних напружень, не виконується. Крім цього, при поперечному згині не виконується лінійний закон Гука(7.6).
Просто практика розрахунків показує, що при поперечному |
згині балок(при певних |
|||||
обмеженнях), можна наближено користуватись формулою дляs |
при чистому |
згині, тобто |
||||
визначати |
|
|
M (x) × y |
|
|
|
|
s= |
|
|
(7.16) |
||
|
I z |
|
||||
|
|
|
|
|
||
Похибка, що виникає при цьому, залежить від відношення довжини балкиl до висоти |
||||||
поперечного перерізу h. При |
l |
³ 4 формула (7.16) повністю |
придатна для |
інженерних |
||
|
||||||
|
h |
|
|
|||
розрахунків.
Нормальні напруження при поперечному згині балки залежать не тільки від координати y точки, але й від координатих перерізу, в якому визначають напруження. Максимальні нормальні напруження виникають у так званому небезпечному перерізі, де M (x) = M max . Тоді в балках з симетричним відносно осі z перерізом
smax = |
M max |
(7.17) |
|
Wz |
|||
|
|
7.6. Дотичні напруження при згині.
При виводі формули для дотичних напружень користуються певними допущеннями, що дозволяють одержати цю формулу за допомогою нескладних методів опору матеріалів. Російський вчений Д.І.Журавський показав, що дотичні напруження досягають порівняно великих значень у перерізах, що мають форму вузьких і високих прямокутників, та у перерізах, які можна розкласти на такі прямокутники. Для таких перерізів можна прийняти дві гіпотези:
а) дотичні напруження tyx в вузьких перерізах мають по всій ширині перерізу вертикальний напрям і рівнодійна їх, що діє в напрямку осі y – це поперечна сила Q(x);
- 48 -

б) по ширині перерізу дотичні напруження tyx |
розподіляються рівномірно. |
||||||||||||||||||
Використавши подані вище гіпотези, одержують формулу для дотичних напружень при |
|||||||||||||||||||
поперечному згині балки |
Q(x) × S zвідс |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
t yx = |
|
|
|
|
|
|
|
(7.18) |
||||||
|
|
|
|
|
|
|
b × I z |
|
|
|
|
|
|
|
|||||
де (рис.7.14 а): |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
tmax = |
3Q(x) |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
y |
|
|
|
|
|
2 |
|
|
|
|
|
z |
|
|
|
|||
|
|
|
b |
|
|
|
|
|
|
|
|
2b h |
|||||||
yC tyx |
|
|
|
|
|
|
y |
|
|
C |
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
Aвідс |
|
|
yC |
|
tyx |
|
|
h |
|
- y |
|
tyx |
|||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||||
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
Aвідс б) |
|
|
|
|
|||||||
|
|
a) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
рис. 7.14. |
|
|
|
|
|
|
|
|
|
||
Q(x) – поперечна сила в перерізі балки;
b - ширина перерізу в тому місці, де знаходять напруження;
= Aвідс × yc - статичний момент відсіченої площі відносно осі z;
- відсічена площа (заштрихована на рисунку площа, що лежить по одну сторону
від точки, в якій визначають напруження); ус - координата центра відсіченої площі.
Дослідження закону зміни дотичних напружень по висоті перерізу показують, що вони змінюються за квадратичним законом. Епюра розподілу tyx по висоті прямокутного перерізу
показана на рис.7.14 б. Для цього перерізу, при визначенні tyx у довільній точці з координатою
|
|
|
|
|
|
|
|
|
|
|
|
|
æ h |
|
|
|
ö |
|
|
|
|
|
|
||||
y маємо |
|
|
|
Авідс |
= b |
|
|
ç |
|
|
|
- y ÷ |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
ø |
|
|
|
|
|
|
||||
|
|
h |
|
1 |
æ h |
|
|
|
|
|
ö |
|
|
1 |
æ h |
ö |
|
|
|||||||||
yc = |
|
|
|
- |
|
|
ç |
|
|
- y |
÷ = |
|
ç |
|
|
|
+ y ÷ |
||||||||||
2 |
|
2 |
2 |
2 |
2 |
|
|||||||||||||||||||||
|
|
|
è |
|
|
|
|
|
ø |
|
|
è |
|
ø |
|
|
|||||||||||
|
|
відс |
|
|
1 |
|
æ h2 |
|
|
|
|
2 |
ö |
|
|
|
|||||||||||
|
S z |
|
|
= |
|
|
b ç |
|
|
|
|
|
- |
y |
|
|
÷ |
|
|
|
|||||||
|
|
|
2 |
|
|
4 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
|
ø |
|
|
|
||||||
|
|
|
|
|
|
|
Iz |
= |
|
bh3 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
3Q(x) |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Найбільше напруження |
|
|
tmax = tyx |
| y=0 = |
. |
||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2b h |
|
Приклад 7.3. Для балки, схема якої показана на рис.7.15 а, що має прямокутний поперечний переріз з розмірами b=8 см, h =16 см, для перерізу в точці А потрібно:
а) визначити нормальне і дотичне напруження в точці “2” перерізу; б) побудувати епюри нормальних і дотичних напружень.
- 49 -
M = 50 kH × м |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
A |
|
|
|
|
B |
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
x |
|
1 м |
F2 = 30 kH |
2 м |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
F1 = 20 kH |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s1 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
10 |
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
1 |
|
|
|
|||||||||
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
|
|
|
|
|
|
|
|
|
2 |
|
|
- |
|||
20 |
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
2 |
|
6 z |
s2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 см |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
30 |
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
8 |
y |
|
|
|
s4 |
||
50 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
50 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
a) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рис. 7.15. |
|
|
|
|
|
|
|
|||||||
Вирази для Q(x) і M(x): |
|
|
|
(0 £ x £ 1 м ) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
AB |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
Q(x) = -F1 = -20 кН ; |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
M (x) = M - F1 × x = 50 - 20x; |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
M(0)=50 кНм; |
|
M(1)=30 кНм. |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
BC |
(1 £ x £ 3 м) |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
Q(x) = -F1 + F2 = 10 кН ; |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
M (x) = M - F1 × x + F2 ×(x -1) = 50 - 20x + 30(x -1); |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
M(1)=30 кНм; |
M(3)=50 кНм. |
|
|
|
|
|
|
|
||||||||||||||||
Епюри Q(x) і M(x) показані на рис.7.15 а. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Визначаємо t2 і s2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
відс |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
M (x) y |
z |
|
|
|
|
|
Q(x) S |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
s2 = |
|
|
|
|
; |
t2 = |
|
|
|
z |
. |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
Iz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bIz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
В перерізі А балки Q(x)=20 кН і M(x)=50 кН. |
|
b h3 |
8 ×163 |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I z |
|
= 2730см |
4 |
|
|||||||||
Для заданого прямокутного перерізу |
|
|
|
= |
|
|
|
= |
|
|
. |
||||||||||||||||||||
|
12 |
12 |
|
||||||||||||||||||||||||||||
Координата точки “2” |
|
у2 = -6 см . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Статичний момент відсіченої площі |
|
|
Szвідс |
= 8 × 2 × 7 = 112 см3 . |
|
|
|
|
|||||||||||||||||||||||
Тоді |
|
50 ×100кН × см ×(-6)см |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
s 2 = |
= -11,0 кН / см2 |
|
|
(стиск) |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
2730 см4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
t2 |
= |
20 кН |
×112 см3 |
|
= |
0,10 кН / см |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
8см × 2730 см4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Найбільше нормальне напруження в даному перерізі
 t2
t2
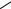 tmax
tmax
- 50 -
