Розрахунок прямокутної пластини при згині

Добавил:

posterp Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Днепропетровский национальный университет железнодорожного транспорта им. академика В. Лазаряна

Предмет:

Сопротивление материалов

Файл:

Пластинки називаються тонкими пластинками, якщо відношення тов-

до найменшого характерного розміру b знаходиться в межах

, а величина найбільшого прогину не перевищує 1 h . Якщо згадане

.pdf

Скачиваний:

Добавлен:

27.04.2021

Размер:

367.36 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ “ЛЬВІВСЬКА ПОЛІТЕХНІКА”

РОЗРАХУНОК ПРЯМОКУТНОЇ ПЛАСТИНИ ПРИ ЗГИНІ ОБЕРНЕНИМ МЕТОДОМ

ЗАВДАННЯ ТА МЕТОДИЧНІ ВКАЗІВКИ до розрахунково-графічної роботи

з курсу “Опір матеріалів” для студентів будівельних спеціальностей

Затверджено на засіданні кафедри «Опір матеріалів», протокол № 4 від 20.11.2008 р.

Львів – 2008

Розрахунок прямокутної пластини при згині оберненим методом. Завдання та методичні вказівки до розрахунково-графічної роботи з курсу “Опір матеріалів” для студентів, будівельних спеціальностей / Укл.: Харченко Є. В., Білобран Б. С., Стасюк Б. М., Мартинович Б. Т., Ліщинська Х. І. – Львів: Видавництво Національного університету “Львівська політехніка”, 2008. – 19 с.

Укладачі:	Харченко Є. В., д-р техн. наук, проф.;
	Білобран Б. С., д-р техн. наук, проф.;
	Стасюк Б. М., канд. фіз.-мат. наук, доц.;
	Мартинович Б. Т., канд. фіз.-мат. наук, доц.;
	Ліщинська Х. І., ас.

Відповідальний за випуск: Харченко Є. В., д-р техн. наук, проф.

Рецензент:

Сокіл Б. І., д-р техн. наук, проф.

Загальні вказівки щодо виконання розрахунково-графічної роботи

1.Розрахунково-графічну роботу виконують на стандартних листах формату А4 (210×297 мм), зшитих зліва.

2.На титульному листі вказують: а) назву навчального закладу; б) назву кафедри; в) назву задачі;

г) шифр академічної групи, прізвище та ініціали студента, який виконує роботу; д) прізвище та ініціали викладача, який керує роботою;

е) місто, календарний рік.

3.На першому листі пишуть умову задачі, наводять числові дані, зображають схему стержня, відкладаючи довжини його ділянок у масштабі і направляючи зовнішні моменти з урахуванням їхніх знаків, вказаних у таблиці.

4.Розрахунки супроводжують лаконічними, чіткими поясненнями.

5.Результати розрахунків наводять, вказуючи одиниці виміру величин.

6.Числові значення підставляють в остаточні залежності, одержані на основі аналітичних перетворень.

7.Розрахунки і пояснення до них, а також рисунки виконують лише на одному боці кожного з листів.

8.У технічних розрахунках не прийнято оперувати простими дробами.

1. Завдання на домашню розрахунково-графічну роботу

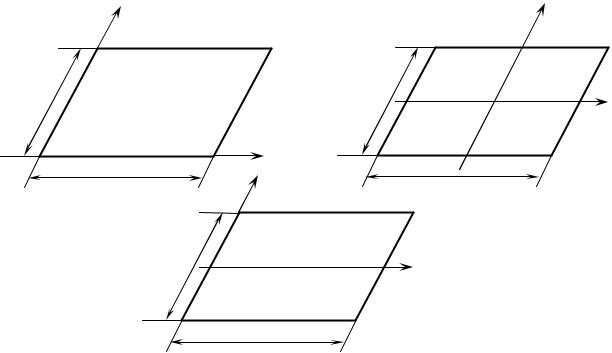
Для заданої прямокутної пластинки (рис. 1), яка знаходиться під дією поперечного навантаження q(x, y) виконати розрахунок на міцність оберненим методом при умові, що задано рівняння зігнутої серединної поверхні пластинки w(x, y). Числові дані геометричних параметрів і навантаження

пластинки взяти з таблиці 1. Вирази навантаження та прогинів пластинки взяти з таблиці 2.

Порядок розрахунку:

1.Використовуючи диференціальне рівняння зігнутої серединної поверхні пластинки, визначити константу С.

2.Встановити , яким граничним умовам задовольняє задане рівняння прогинів w(x, y).

3.Побудувати вирази для згинальних та крутних моментів, а також для поперечних сил.

4.Побудувати епюри моментів та поперечних сил в перерізі, вказаному в

таблиці 1.

5. По побудованих епюрах визначити найбільші значення напружень

σx ,σy ,τxy .

y			y
b		2b	x
			0
	x
0	y
a	y		2a
Схема 1.			Схема 2.
	2b		x

Схема 3.

Рис. 1. Схеми прямокутних пластинок.

Таблиця 1

Числові значення геометричних параметрів і складових навантаження

№	Розміри пластинки, м			Координати		q0 ,kH м	2	ν
№	Розміри пластинки, м			перерізу, м		q0 ,kH м
варіанту				перерізу, м
варіанту	a	b	h	x	y
	a	b	h	x	y
1	4	3	0,1	1	-	50		0,25

2	5	4	0,15	-	0,5	60		0,3

3	6	4	0,2	1,5	-	70		0,25

4	5	2	0,25	-	0,75	80		0,3

5	6	3	0,1	2	-	90		0,25

6	4	2	0,15	-	1	100		0,3

7	4	2	0,2	0,5	-	110		0,25

8	5	3	0,25	-	1,25	120		0,3

9	6	2	0,1	2,5	-	130		0,25

10	5	4	0,15	-	1,5	140		0,3

11	4	4	0,2	1	-	130		0,25

12	6	5	0,25	-	0,5	120		0,3

13	6	2	0,1	1,5	-	110		0,25

14	5	3	0,15	-	0,75	100		0,3

15	4	4	0,2	0,5	-	90		0,25

16	4	2	0,25	-	0,5	80		0,3

17	5	5	0,1	2	-	70		0,25

18	6	3	0,15	-	1	60		0,3

19	6	2	0,2	1	-	50		0,25

Таблиця 2

Навантаження та прогини пластинки

№

Функція навантаження

Рівняння зігнутої

Схема

варіанту

пластинки

серединної поверхні

q (x, y)= q sin

π x

sin

2π y

w(x, y)= C sin

π x

sin

2π y

q(x, y)

= q

sin π x sin π y

w(x, y)= C sin π x sin π y

q (x, y)= q sin

2π x

sin

2π y

w(x, y)= C sin

2π x

sin

2π y

q (x, y)= q sin

2π x

sin

π y

w(x, y)= C sin

2π x

sin

π y

q (x, y)= q0

w(x, y)= C x y (x −a)(y −b)

q(x, y)= q0 π

x(x −a)−4 sin

π y

w(x, y)= C x (x −a)sin

π y

q(x, y)= q0 π

y(y −b)−4 sin

π x

w(x, y)= C y (y −b)sin

π x

q (x, y)= q0

w(x, y)= C (x −a)2 (y −b)2

4π

2πy

q(x, y)=q0

(x −a)

−4 sin

w(x, y)= C (x −a)

sin 2 y

4π2

(y −b)

2πx

w(x, y)= C (y −b)

sin

2πx

q(x, y)=q0

−4 sin

q (x, y)= q0

w(x, y)=C (x2 −a2 )(y2 −b2 )

q(x, y)= q0 π

(x2 −a2 )−4 sin

πy

w(x, y)= C (x2 −a2 )sin

π y

q(x, y)= q0 π

(y2 −b2 )−4 sin

πx

w(x, y)= C (y2 −b2 )sin

πx

q(x, y)=q0

π2

(x2 −a2 )−4 cos

πy

w(x, y)= C (x2 −a2 )cos

π y

π2

πx

q(x, y)=q0

−b

)−4 cos

w(x, y)= C (y

−b

)cos

q (x, y)= q0

w(x, y)= C (x −a)2 (y −b)2

π2

πy

π y

q(x, y)= q0

(x −a)

−4 cos

w(x, y)= C (x −a)

cos

q(x, y)=q0 4π22

x(x −a)

−4 sin 2πy

w(x, y)= Cx(x −a)sin 2π y

π2

x(x −a)

πy

q(x, y)= q0

−4 cos

w(x, y)=Cx(x −a) 1+cos

Основні теоретичні відомості.

Пластинкою називають тіло призматичної або циліндричної форми, висота якого h мала порівняно з двома іншими розмірами. Розмір h називають товщиною пластинки. В інженерній практиці здебільшого використовують пластинки сталої товщини. Хоча можливе також проектування конструкцій з використанням пластинок змінної товщини. Поверхня, яка розділяє пластину навпіл по товщині, називається серединною поверхнею. Розглянемо згин призматичних пластин, для яких серединна поверхня є площиною. Вважаємо, що матеріал пластинки є пружним, однорідним і ізотропним.

співвідношення є меншим, то таку пластинку називають мембраною, а якщо більшим – плитою. Тоді рівняння для розрахунку таких пластин вже повинні враховувати значні прогини в першому випадку та суттєву зміну напружень по товщині пластини - в другому. Для розрахунку тонких пластин застосовується технічна теорія згину пластин, яка ґрунтується на трьох гіпотезах Кірх-

гофа:

1)Гіпотеза прямих нормалей: Прямолінійний елемент пластинки перпендикулярний до її серединної поверхні залишається прямим і перпендикулярним до неї і після деформування. Ця гіпотеза є аналогом принципу плоских перерізів в стрижневих конструкціях і дозволяє нехтувати зсувом на на- пружено-деформований стан пластинки.

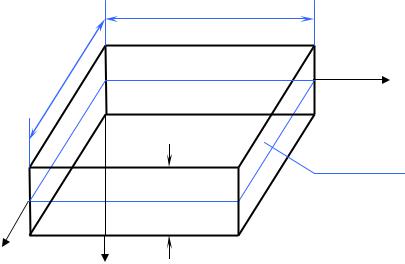
2)Гіпотеза недеформівності серединної площини: Зміною довжини

y	h
z	Рис. 2.

Серединна

площина

перпендикулярного до серединної площини елемента можна знехтувати

(εz = 0 ).

3) Гіпотеза відсутності тиску між шарами пластинки: Нор-

мальними напруженнями перпендикулярними до серединної поверхні можна знехтувати (σz = 0 ).

Ця гіпотеза дозволяє

звести задачу до плоского напруженого стану.

При розв’язуванні задач згину прямокутної пластинки використовуєть-

ся прямокутна декартова система координат. Осі x

і y розташовані в сере-

динній площині (рис. 2) пластинки, а вісь z

направляється вниз перпендику-

лярно до серединної площини.

Через u,v, w позначимо переміщення точок пластинки в напрямку осей

координат x, y, z

відповідно. Основним переміщенням при згині пластинки є

прогин w (переміщення в напрямку осі z ).

Циліндричним згином пласти-

нки називають такий вид деформу-

вання, при якому серединна повер-

хня набуває циліндричної форми.

Наприклад, коли умови закріплен-

ня і величина навантаження не змі-

нюються по координаті y .

В поперечному перерізі плас-

тинки

виникають

два

внутрішні

згинальні

моменти

та

поперечні

M x

сили.

Зазначимо,

що індекси біля

згинальних

моментів

вказують не

на вісь, відносно якої він повертає,

σx

а на нормаль до перерізу, в якому

він виникає ( M x - погонний момент

в перерізі з нормаллю x ). Ці зусил-

σy

ля виражаються через напруження

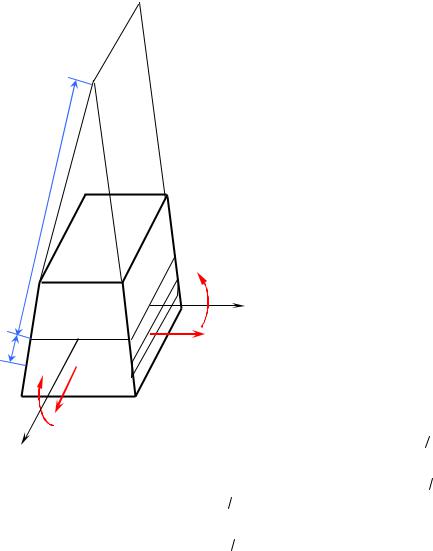
таким чином (рис. 3):

y M y

Рис. 3.

h 2

M x = ∫ σx z d z ;

−h 2

h 2

M y = ∫ σy z d z .

(1)

−h 2

Геометричні співвідношення при згині пластини:

εx = (z + ρ)d x − ρd x =

;

εy = 0 .

(2)

ρd x

Фізична сторона задачі (Закон Гука):

εx =

(σx −νσy ); εy

(σy

−νσx ).

(3)

Враховуючи всі ці співвідношення отримаємо:

σy =νσx ;

(σx −ν2 σx );

z E

E z

−d

σx =

ρ 1 −ν

1 −ν

d x

З іншого боку напруження виражається через згинальний момент наступним чином:

σx =	M	x z ,	σy =	M y	z ,	(4)
	I1			I2

де I	= I	2	=	h3	- моменти інерції поперечного перерізу пластини шириною
1		2		12
				12

одиниця. Тоді диференціальні співвідношення між внутрішніми зусиллями та функцією прогинів пластинки запишуться наступним чином:

= −D

∂2w

;

= −ν D

∂2w

(5)

∂x2

де

D =

E h3

- циліндрична жорсткість пластинки,

E , ν - модуль пружно-

(

)

12 1−ν

сті та коефіцієнт Пуассона матеріалу пластинки, а згинальні моменти є віднесеними до одиниці ширини пластинки.

Із виразів (4) видно, що нормальні напруження σx ,σy змінюються по висоті перерізу за лінійним законом. Вони набувають найбільших значень в то-

чках, які прилягають до поверхні пластинки (z = ±h

) , а на серединній пове-

рхні дорівнюють нулеві, тобто:

6M y

maxσ

;

maxσ

(6)

В загальному випадку згину пластин будемо мати викривлення серединної поверхні як відносно осі x , так і відносно осі y . Це означає, що лінійні дефо-

рмації εx та εy відмінні від нуля і рівні:

;

(7)

Виразивши з формул (3) напруження

σx =

(εx +ν εy );

σy

(εy +ν εx ),

(8)

(

−ν

)

(

−ν

)

отримаємо

1 / 21 2 > Следующая >>>

Соседние файлы в предмете Сопротивление материалов

#
27.04.2021404.62 Кб3Расчет_статически_неопределимых_систем_методом_сил_Метод_указания_Хлебородов_2001.pdf
#
27.04.2021764.85 Кб5Розрахунок балок при прямому згині.pdf
#
27.04.2021881.99 Кб1Розрахунок валу на витривалість.pdf
#
27.04.2021467.11 Кб1Розрахунок геометричних характеристик.pdf
#
27.04.2021504.53 Кб8Розрахунок просторової рами.pdf
#
27.04.2021367.36 Кб8Розрахунок прямокутної пластини при згині.pdf
#
27.04.2021307.12 Кб6Розрахунок стиснутих стрижнів на стійкість.pdf
#
27.04.2021420.21 Кб1Розрахунок стрижнів при крученнi.pdf
#
27.04.2021314.72 Кб7Частина1.pdf
#
27.04.2021302.3 Кб2Частина2.pdf
#
27.04.2021367.64 Кб3Частина3.pdf