
Частина2
.pdf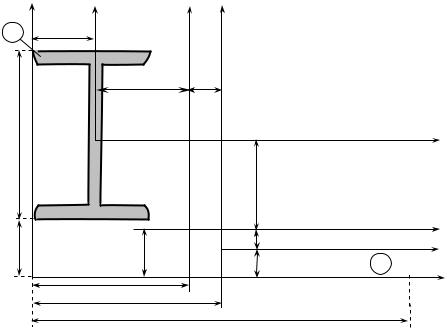
Розміри профілів і всі їх геометричні характеристики приводяться в спеціальних таблицях, в залежності від номеру профілю. Ці таблиці наведені у всіх підручниках з опору матеріалів чи в довідниках.
Приклад 4.1. |
Для показаного на рис.4.5 перерізу, що складається із двотавра № 16 і прямокут- |
||||||||
|
y0 |
y2 |
yC |
y |
ника, визначити положен- |
||||
2 |
4,5 |
|
|
1 |
ня |
центра |
і |
обчислити |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
значення |
моментів |
інерції |
|||
|
|
|
|
|
|||||
|
|
|
|
|
відносно |
горизонтальної і |
|||
|
|
7,97 |
|
1,53 |
вертикальної |
центральних |
|||
|
|
|
|
|
осей. |
|
|
|
|
16 |
|
C2 |
|
|
|
z2 |
|
|
|
|
|
||
|
|
|
|
8,39 |
|
|
|
|
|
|
|
|
zC |
|
|
C |
|
1,61 |
|
|
4 |
|
C1 |
|
z1 |
||
|
3,61 |
2 |
1 |
|||
|
|
|
|
z0 |
||
|
O |
12,47 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
14 |
28 |
|
|
|
|
|
|
|
|
|
|
|
|
|
рис.4.5. |
|
|
|
Заданий складний переріз розбиваємо на дві прості частини: двотавр і прямокутник.
Для двотавра №16 (частина 2) із таблиці сортаменту виписуємо дані :
b = 9 см ; h = 16 см;
А2 = 21,5 см2 ; I z2 = 945 см4 ; I y2 = 77,6 см4 .
Для прямокутного перерізу (частина 1) b = 28 см ; h = 16 см;
А = 21,5см2 |
; I |
z |
= |
b h3 |
= |
28 × 43 |
=149,3см4 ; |
I |
y |
= |
h b3 |
= |
4 × 283 |
= 7317,3см4. |
|
|
|
|
|||||||||||
1 |
|
12 |
12 |
|
|
12 |
12 |
|
||||||
|
|
1 |
|
|
1 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Положення загального центра всього складного перерізу, що складається х двох простих частин : частина 1 (прямокутник) і частина 2 (двотавр) відносно довільних допоміжних осей z0 , y0 знайдемо, використавши формули (4.4)
|
|
åS y0 |
|
(1) |
(2) |
|
|
112 ×14 + 21,5 × 4,5 |
|
1664,75 |
|
|
||||||
zc |
= |
= |
S y0 |
+ S y0 |
= |
|
|
см; |
||||||||||
å A |
|
|
|
|
|
|
= |
|
|
= 12,47 |
||||||||
A1 + A2 |
|
112 + 21,5 |
|
|
133,5 |
|||||||||||||
|
|
åS z0 |
|
(1) |
(2) |
|
|
112 × 2 + 21,5 ×12 |
|
|
482 |
|
|
|
||||
yc |
= |
= |
S z0 |
+ S z0 |
|
= |
= |
= 3,61 см. |
|
|||||||||
å A |
|
|
|
|
|
|
|
|||||||||||
A1 + A2 |
|
|
112 + 21,5 |
133,5 |
|
|||||||||||||
Відкладаємо знайдені значення координат центру, визначаємо центр перерізу (точка С) і проводимо вертикальну і горизонтальну центральні осі (осі yc , zc ).
Величини моментів інерції відносно осей yc , zc обчислимо за формулами паралельного переносу (4.9), перейшовши від центральних осей y1 , z1 першої частини і y2 , z2 другої частини до осей yc , zc .
I |
z |
|
= I (1) |
+ a 2 A |
+ I ( |
2) |
+ a 2 A |
; |
I |
y |
|
= I (1) |
+ b2 A |
+ I (2) |
+ b2 A ; I |
y z |
|
= I (1) |
+ a b A + I (2) |
+ a b A |
||
|
c |
z |
1 1 |
z |
2 |
2 2 |
|
|
c |
y |
1 1 |
y |
2 |
2 2 |
c |
y z |
1 1 1 |
y z |
2 2 2 |
|||
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
c |
1 1 |
|
2 2 |
|
|||||
де а1 = - 0,39 см , в1 =1,53 - координати центра С1 відносно осей zc , yc ;
а2 =8,39 см , в2 =- 7,97 - координати центра С2 відносно осей zc , yc ;
- 31 -
відцентрові моменти: I |
(1) |
|
першої частини |
відносно осей y z |
і I |
(2) |
другої частини відносно |
||
|
y z |
|
1 1 |
|
y |
z |
2 |
|
|
|
1 |
1 |
|
|
|
2 |
|
|
|
осей y2 z2 дорівнюють нулеві, бо осі y1 z1 і y2 z2 є головними центральними осями для першої і другої частин перерізу.
Тоді
I zc = 149,3 + (-1,61)2 ×112 + 945 + 8,392 × 21,5 = 2898,0 см4
I yc = 7317,3 +1,532 ×112 + 77,6 + (- 7,97)2 × 21,5 = 9022,8 см4
I yc zc = 0 + (-1,61)×1,53 ×112 + 0 + 8,39 × (- 7,97)× 21,5 = -1713,0 см4
y0 y1 y2 yC |
|
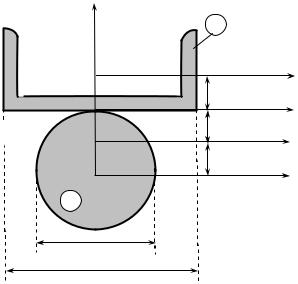
Приклад 4.2. Для зображеного на рис.4.6 пе- |
||||||||||
2 |
|
рерізу, що складається з швелера №20 і кру- |
||||||||||
|
|
га, знайти положення головних центральних |
||||||||||
|
z2 |
осей і обчислити значення головних моментів |
||||||||||
|
інерції. |
|
|
|
|
|
|
|
|
|
|
|
2,07 |
|
|
|
|
|
|
|
|
|
|
|
|
zC |
z0 |
Для круга (частина 1 перерізу) визначаємо |
||||||||||
= -3,38 |
|
|
p × d 2 |
|
3,14 ×102 |
|
|
|
||||
|
zC |
A1 |
= |
= |
=78,5 см |
2 |
; |
|||||
a1 = -1,62 |
|
4 |
|
|
4 |
|
||||||
|
|
|
|
|
|
|
|
|||||
|
z1 |
I z |
= I y =0,05 × d 4 =0,05 ×104 =500 см4 . |
|||||||||
1 |
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для швелера №20 (частина 2 перерізу) знахо- |
||||||||||
10 |
|
димо із таблиць |
|
|
|
|
|
|
|
|||
|
A |
= 23,4 см2 ; z |
|
= 2,07 см;b =7,6 см ; |
||||||||
|
|
0 |
||||||||||
20 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
I z2 |
=113см4 ; I y2 |
=1520 см4 . |
|
|
|||||||
рис.4.6.
Положення центру всього перерізу визначаємо відносно довільних осей y0 z0 . Так як вісь y0 - це вісь симетрії перерізу, то центр перерізу
буде лежати на цій осі. Тому визначаємо тільки одну координату центра yc
|
åS z0 |
|
(1) |
(2) |
|
78,5 ×(-5) + 23,4 |
× 2,07 |
|
- 344 |
|
yc = |
= |
S z0 |
+ S z0 |
= |
= |
=- 3,38 см . |
||||
å A |
|
|
|
|
|
|||||
A1 |
+ A2 |
78,5 + 23,4 |
|
101,9 |
За визначеними координатами наносимо центрС і проводимо вертикальну і горизонтальну центральні осі yc , zc . Оскільки вертикальна вісьyc є віссю симетрії, то ця вісь і перпен-
дикулярна до неї вісь zc , що проходить через центр – це головні центральні осі. Відцентровий момент I yc zc відносно них дорівнює нулеві. Визначаємо головні моменти I zc , I yc , скористав-
шись формулами паралельного переносу
I |
z |
|
= I (1) |
+ a 2 |
× A |
+ I (2) |
+ a 2 |
× A |
=500 + (-1,62)2 ×78,5 +113 + 5,452 × 23,4 =1514 см4 |
|
|
c |
z |
1 |
1 |
z |
2 |
2 |
2 |
|
|
|
|
1 |
|
|
|
|
|
|
||
I |
y |
|
= I (1) |
+b2 |
× A |
+ I (2) |
+b2 |
× A |
=500 + 0 +1520 + 0 =2020 см4 . |
|
|
c |
y |
1 |
1 |
y |
2 |
2 |
2 |
|
|
|
|
1 |
|
|
|
|
|
|
||
- 32 -
V.Зсув.
5.1.Напруження і деформації. Розрахунок на міцність.
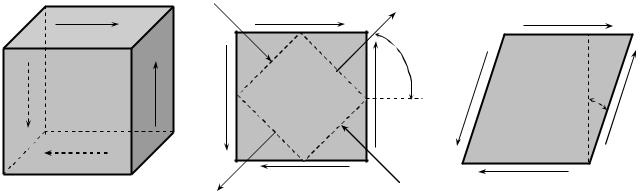
Окремий випадок плоского напруженого стану, при якому на гранях елементарного кубика, виділеного з тіла, виникають лише дотичні напруження (рис.5.1 а, б) називається чистим зсувом.
τ |
τ |
σ1 = τ |
τ |
|
τ |
a = 45o |
|
|
|
|
|
|
|
|
γ |
|
|
τ |
τ |
|
|
|
|
|
|
σ3 =- τ |
|
a) |
б) |
|
в) |
|
рис. 5.1. |
|
|
Величина і напрям головних напружень (рис.5.1 б), що визначаються за формулами (3.4) і (3.5), у цьому випадку рівні
s1 =t ;s 3 = -t ; (s 2 =0 );a = ± 450 .
Тобто чистий зсув можна реалізувати шляхом розтягу і стиску у двох взаємоперпендикулярних напрямах.
За теорією міцності найбільших дотичних напружень (III теорія) умова міцності набирає
вигляду |
s IIIекв = s1 - s3 £ [s ] , |
|
|
або |
s IIIекв = t - (-t ) £ [s ] , |
звідки |
s IIIекв = 2t £ [s ] . |
Ввівши позначення [s ]=[t ], отримуємо умову міцності
2
t £ [t ]
(5.1)
За IV теорією міцності отримуємо ту ж умову міцності(5.1), тільки [t ]=0,6 ×[s ].
Дотичні напруження t при зсуві в межах пружних деформацій зв’язані з деформаціями зсуву g (рис.5.1 в) лінійною залежністю
t =G ×g , |
(5.2) |
яка носить назву закону Гука при зсуві.
Стала G, що називається модулем зсуву матеріалу виражається через модуль пружності E і коефіцієнт Пуассона m
G = |
|
E |
|
(5.3) |
|
2 ×(1+ m) |
|||||
|
|
||||
Для сталі з модулем E = 2, 0 ×105 |
МПа і коефіцієнтом m =0,3 модуль G дорівнює |
|
|||
- 33 -
G = |
|
2,0 ×105 |
= 8,0 ×104 МПа . |
|
× (1 + 0,3) |
||
2 |
|
||
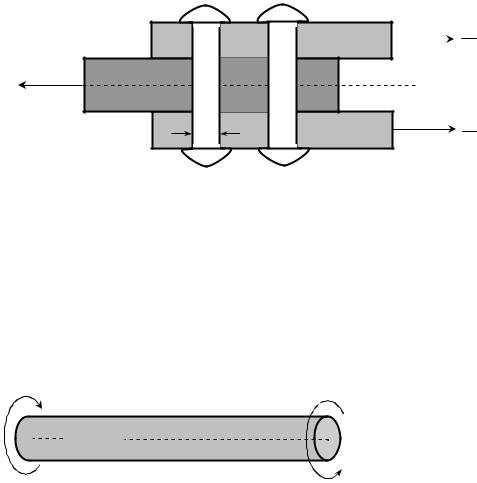
Умову міцності при зсуві(5.1) використовують при розрахунках на міцність елементів конструкцій, що з’єднані між собою заклепками чи зваркою. В таких елементах руйнування відбувається у формі зрізу заклепок або зварного шва. Умова міцності набирає вигляду
|
tmax = |
|
N |
£ [t ] |
|
|
(5.4) |
||
|
|
|
|
|
|||||
|
|
|
|
|
зр |
|
|
|
|
|
|
|
Aзр |
|
|
|
|||
де А зр |
- сумарна площа зрізу; [t ] зр - допустиме напруження на зріз. |
|
|
||||||
У випадку заклепочного з’єднання (рис.5.2) площа зрізу дорівнює |
|
||||||||
|
|
p × d 2 |
|
|
|
||||
|
А зр = |
|
|
|
× n зр × n |
|
|
(5.5) |
|
|
4 |
|
|
p× d 2 |
|||||
|
|
|
|
|
|
||||
де n зр |
– кількість площин зрізу однієї заклепки (на рис.5.2 n зр |
=2); |
- площа попереч- |
||||||
4 |
|||||||||
|
|
|
|
|
|
|
|
||
|
N |
|
|
2 |
|
N |
|
|
d |
N |
|
2 |
||
|
||
|
рис. 5.2. |
ного перерізу однієї площини зрізу; n – кількість заклепок в з’єднанні (на рис.5.2
n= 2 ).
Впрактичних розрахунках умова міцно-
сті |
найчастіше |
-слу |
|
жить |
для |
визначення |
|
необхідної |
кількості |
||
заклепок n. |
|
|
|
VI. Кручення.
6.1.Крутні моменти.
Зкрученням на практиці зустрічаються при розрахунку осей рухомого складу, осей трансмісії, пружин і т.д. У найпростішому випадку деформація кручення викликається двома протилежно напрямленими парами сил, що діють у площинах, перпендикулярних до осі стержня (рис.6.1). Стержень, що працює на кручення називають валом.
M |
Зовнішні моменти, що закручують |
||
вал, називатимемо закручуючими |
момен- |
||
|
тами. Під дією цих моментів в попере- |
||
|
чних перерізах вала, як протидія, виника- |
||
|
ють внутрішні моменти М к |
- крутні мо- |
|
рис. 6.1. |
M менти. Для визначення цих |
моментів ви- |
|
|
користовується метод перерізів. За |
допо- |
|
могою цього методу можна сформулювати наступне правило для визначення крутних моментів:
Крутний момент М к у довільному поперечному перерізі вала чисельно дорівнює алге-
браїчній сумі закручуючих моментів, прикладених до вала з якоїсь однієї сторони від даного перерізу. При цьому додатним вважаються ті моменти, що обертають проти ходу стрілки годинника, коли дивитись вздовж зовнішньої нормалі до перерізу.
- 34 -
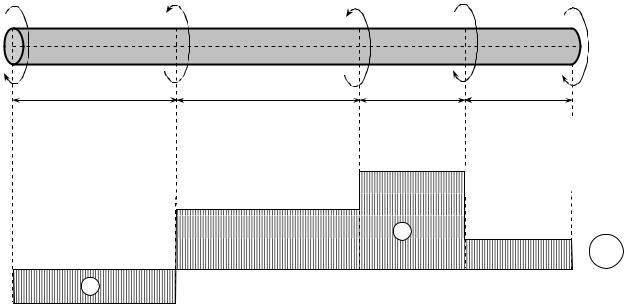
Графік розподілу крутних моментів по довжині вала називаюепюроють |
крутних моментів |
М к . |
|
Приклад 6.1. Побудувати епюру крутних моментів для вала, що зображений на рис.6.2.
M 1 = 10 kH × м |
M 2 = 30 kH × м |
M 3 = 10 kH × м M 4 = 20 kH × м M 5 = 10 kH × м |
||
A |
B |
C |
Д |
E |
|
2 м |
2 м |
1 м |
1 м |
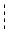 30
30
20 |
10 |
+ |
M k
-
10
рис. 6.2.
Вирази для крутних моментів на ділянках вала :
МКАВ = -М1 = -10 кНм ;
МКВС = -М1 + М 2 = 20 кНм ;
МКСD = -М 1 + М 2 + М 3 = 30 кНм ;
МКDЕ = -М1 + М 2 + М 3 + М 4 = М 5 = 10 кНм ;
Епюра М к зображена на рисунку.
Для визначення величини крутних моментів потрібно знати величину моментів зовнішніх пар сил, що передаються на вал. Нерідко в інженерній практиці ці пари невідомі, але відомі потужності N, що передаються валом і швидкість обертання вала.
Якщо потужність N задана в кіловатах (кВт), а n в обертах за хвилину, то закручуючий
момент М дорівнює: |
|
||
М =9,55× |
N (кВт) |
=...(кНм) |
(6.1) |
|
|||
|
n(об / хв) |
|
|
6.2. Напруження при крученні вала круглого поперечного перерізу.
Крутний момент М к , який в попередньому параграфі виражався через закручуючі моменти зовнішніх сил, являє собою сумарний момент елементарних пар внутрішніх сил tr × dA ×r. зв’язаних з дотичними напруженнями tr , що виникають у довільній точці перерізу (рис.6.3), тобто
- 35 -

M k |
|
dA |
M k = òtr × dA ×r = òtr × r × dA |
(6.2) |
|
||||
|
|
|||
|
|
При цьому вважається, що дотичні напруження tr перпендику- |
||
r |
|
|
||
|
tr |
лярні до вектора r . |
|
|
|
|
|
||
|
|
|
Останній вираз дає інтегральну залежність між крутним момен- |
|
|
|
|
том М к і дотичними напруженнями tr |
в перерізі вала. Ця залежність |
|
|
|
може задовольнятись при різних законах розподілуtr . Для того, щоб |
|
рис. 6.3. |
визначити величину tr із виразу (6.2) |
потрібно знати дійсний закон |
||
|
|
|
розподілу дотичних напружень у поперечному перерізі. Цей закон мож- |
|
на одержати лише на основі дослідних даних.
Якщо закручувати вал довільного поперечного перерізу, то плоскі до початку навантаження поперечні перерізи при навантаженні перестають бути плоскими, депланують. Лише при крученні стержнів круглого або кільцевого поперечних перерізів депланації відсутні. Для таких перерізів, на основі дослідних даних, встановлено, що при крученні:
а) поперечні перерізи вала, залишаючись плоскими і перпендикулярними до його ,осі повертаються один відносно одного на певний кут, що називається кутом закручування j ;
б) віддаль між перерізами при закручуванні не змінюється; в) прямі лінії (радіуси), проведені у поперечних перерізах вала при закручуванні не ви-
кривляються, тобто залишаються прямими.
Якщо використати ці факти і взяти до уваги, що при крученні має місце деформація зсуву і виконується закон Гука при зсуві (5.2), то отримаємо наступний закон зміни tr в поперечному перерізі вала
|
|
|
|
tr =G × gr |
=G × |
dj |
× r |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
(6.3) |
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Підставивши останній вираз для tr в формулу (6.2), одержуємо |
|
|
|
|
|
||||||||||||||
|
|
|
|
dj |
M k |
|
|
|
|
|
|
|
|
|
|
|
(6.4) |
|
||
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
dx |
G × I p |
|
|
|
|
|
|
|
|
|
|
|||||
|
де I p = òr2 × d A - полярний момент інерції поперечного перерізу вала (див 4.3). |
|
|
|||||||||||||||||
|
A |
|
|
|
|
|
|
|
|
Після |
підстановки виразу |
|||||||||
|
tmax |
|
|
|
tmax |
|
|
|||||||||||||
|
|
|
|
для |
|
dj |
із |
|
співвідношення(6.4) |
в |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
tr |
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
рівняння (6.3), отримуємо формулу |
|||||||||||||
|
r |
|
|
|
|
|
|
для |
|
дотичного напруження |
при |
|||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
d |
кручення вала круглого перерізу: |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
tr = |
M k ×r |
|
(6.5) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I p |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Епюри дотичних напружень |
||||||
tmax |
|
|
tmax |
|
|
|
|
|
|
tr |
для круглого і кільцевого пере- |
|||||||||
|
|
|
|
|
|
|
|
різів вала показані на рис.6.4. |
|
|||||||||||
|
d |
|
|
|
|
|
D |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
a) |
б) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
рис. 6.4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
- 36 -
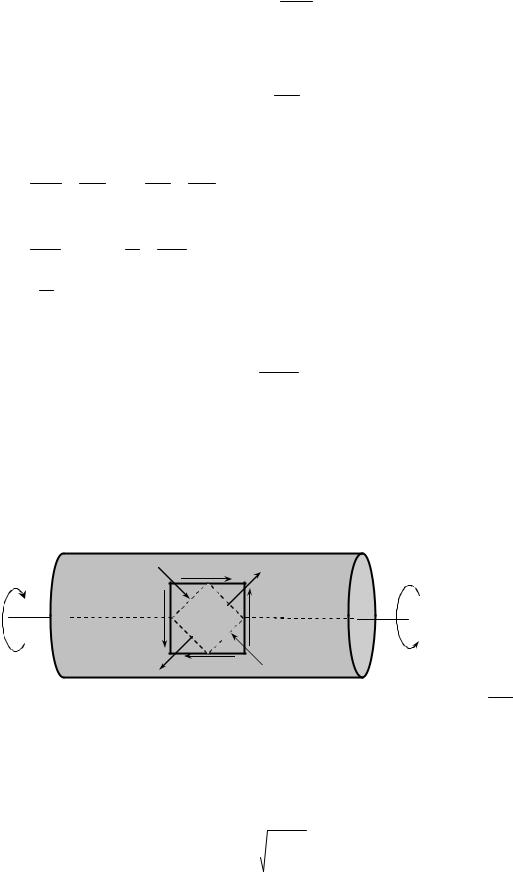
Максимальне дотичне напруження виникає при |
r =rmax . Якщо ввести позначення |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
I p |
=Wp |
|
|
|
|
|
|
(6.6) |
|
|
|
|
|
|
|
|
|
|
rmax |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
де Wp - геометрична характеристика, |
що називається полярним моментом опору поперечного |
||||||||||||||||||
перерізу, то формула для визначення tmax |
набирає вигляду |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
tmax |
= |
M k |
|
(6.7) |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
Wp |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для круглого поперечного перерізу вала з радіусом r і діаметром d (рис.6.4а) полярний момент |
|||||||||||||||||||
опору |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I p |
= |
pr 4 |
pr 3 |
pd 3 |
0,2d |
3 |
|
|
|
|
|
(6.8) |
|
|
|
|
|||
Wp = |
|
¸ r = |
= |
» |
|
|
|
|
|
|
|
|
|
|
|||||
rmax |
|
|
2 |
2 |
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для кільцевого перерізу (рис.6.4б) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Wp = pD4 (1 - a4 )¸ D = pD3 (1 - a4 )» 0,2D3 (1 - a4 ), |
|
|
(6.9) |
|
|
||||||||||||||
32 |
|
|
2 |
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
де a = d . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вираз (6.4) служить для виведення формули для величини кута закручення j одного кінцевого |
|||||||||||||||||||
перерізу вала довжиною l відносно другого. Інтегруючи цей вираз, одержимо |
|
|
|||||||||||||||||
|
|
|
|
|
|
j = |
M k ×l |
|
|
|
|
|
|
|
|
(6.10) |
|||
|
|
|
|
|
|
G × I p |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
6.3. Розрахунок валів на міцність і жорсткість. |
|
|
|
|
|
|
|
|
|||||||||||
При крученні вала, на його поверхні має місце напружений стан чистого зсуву з напру- |
|||||||||||||||||||
женнями tmax |
(рис.6.5), що обчислюються за формулою (6.7). Головні напруження в цьому ви- |
||||||||||||||||||
падку s1 =tmax ;s2 =0;s3 =- tmax . Якщо при розрахунку на міцність використати III теорію мі- |
|||||||||||||||||||
цності, то умова міцності набирає вигляду |
|
|
|
|
|
sIII |
|
|
£ [s] |
||||||||||
|
|
|
σ3 = -τmax |
|
|
|
|
|
|
|
|
|
|
= s - s |
3 |
||||
|
|
|
|
|
σ1 = τmax |
|
|
|
|
екв |
1 |
|
|||||||
M k |
|
|
|
|
|
|
|
або |
sеквIII |
= 2 × tmax £ [s]. |
|||||||||
|
|
|
|
|
|
|
τmax |
|
|
|
|
Звідки tmax £ 0,5 ×[s]. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Якщо |
|
ввести |
|
позначення |
|
|
|
|
|
σ1 |
τmax |
|
|
σ3 |
|
|
|
M k |
0,5 ×[s]=[t], то умова міцнос- |
||||||
|
|
|
|
|
|
|
|
|
ті набирає вигляду |
|
|
||||||||
|
|
|
|
|
рис. 6.5. |
|
|
|
|
|
|
|
tmax |
= M k |
£ [t ] |
|
(6.11) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Wp |
|
|
|
|
||
Якщо при розрахунку на міцність використатиIV теорію міцності, то умова міцності |
|||||||||||||||||||
(6.11) залишиться без зміни, якщо прийняти |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
[t]= 0,58 ×[s]. |
|
|
|
|
|
|
|
|
|||||
Підставивши в умову міцності(6.11) значення Wp із формул (6.8), (6.9), отримаємо ви-
рази для підбору d круглого вала
d ³ 3 |
M k |
|
(6.12) |
|
0,2[t ] |
||||
|
|
|||
- 37 -
і діаметрів D і d кільцевого вала
|
M k |
(6.13) |
D = 3 |
0,2[t ]×(1- a4 ); d = aD. |
Зауважимо, що при передачі великих закручуючих моментів вали кільцевого перерізу є більш раціональні. Про це свідчать епюри t (рис.6.4) для круглих і кільцевих валів. З епюри t для круглих валів видно, що матеріал вала, який розташований біля осі вала, майже не працює.
Вкільцевому валі цей матеріал відсутній.
Вдеяких випадках, крім розрахунку на міцність, є необхідність виконати і розрахунок вала на жорсткість. Перевірка жорсткості полягає в порівнянні максимального кута закручування
віднесеного до одиниці довжини вала qmax з допустимим відносним кутом закручування [q]:
qmax £ [q], |
(6.14) |
де qmax = max j . l
Кут закручування j в радіанах обчислюється з формули (6.10).
Оскільки допустимі кути закручення [q] найчастіше задаються в градусах, то перейшовши в виразі (6.14) до градусів, одержуємо умову жорсткості
M k |
× |
1800 |
£ [q ]0 |
(6.15) |
|
GI p |
p |
||||
|
|
|
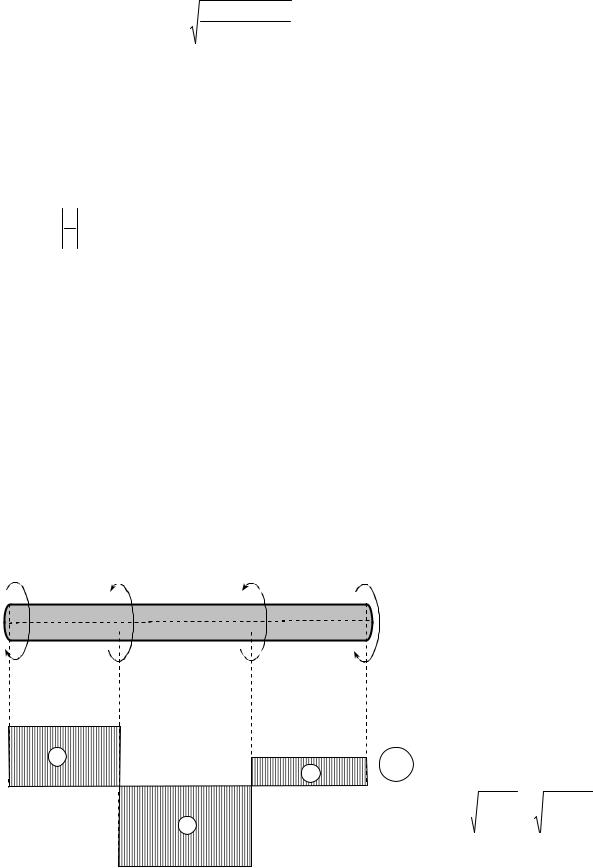
Приклад 6.2. Для зображеного на рис. 6.6 вала круглого поперечного перерізу побудувати епюру крутних моментів, та, виходячи з умови міцності, підібрати діаметр вала, якщо
[t ] = 6 кН / см2 .
Знаходимо величини крутних моментів на ділянках вала
M KAB = M1 = 10 кНм ;
M KBC = M1 - M 2 = -30 кНм ;
M KCD = M1 - M 2 + M 3 = 20 кНм .
M 4 = 20 kH × м M 3 = 50 kH × м M 2 = 40 kH × м M1 = 10 kH × м
Д  C
C  B
B 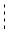 A
A
|
20 |
|
+ |
10 |
M k |
|
+ |
-
30
За цими даними побудована епюра М к .
Як видно з епюриМ к
найбільший крутний момент виникає на ділянці
BC : max М к =30 кНм.
Розрахунок на міцність виконуємо для цього моменту. Діаметр круглого вала, знайдений із виразу
(6.12) :
d ³ 3 |
M k |
|
= 3 |
30 ×100 |
; |
0,2[t ] |
0,2 ×6 |
||||
d ³ 13, 5 см .
рис. 6.6.
- 38 -
VII. Прямий згин.
7.1. Основні поняття. Навантаження і закріплення балок.
|
Стержень з прямою віссю, що працює на згин, називають балкою. Ознакою деформації |
|||||||||||||||
згину є зміна кривизни балки. Згин, |
при якому скривлення осі відбувається в одній з її голо- |
|||||||||||||||
y |
|
F |
q |
|
|
|
|
вних площин, |
|
тобто |
у пло- |
|||||
|
|
|
|
|
|
|||||||||||
|
M |
|
щині, утвореній віссю балки |
|||||||||||||
|
|
|
|
|
|
|
|
|
і однією з головних центра- |
|||||||
|
|
|
|
|
|
|
|
|
льних |
осей |
|
її |
поперечного |
|||
x |
|
|
|
|
|
|
|
а) |
перерізу, |
називають |
прямим |
|||||
|
|
z |
|
|
|
|
|
|
згином. Коли ж зігнута вісь |
|||||||
|
|
|
|
|
|
|
|
балки не лежить в головній |
||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
площині, то згин називають |
|||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
косим |
|
згином. |
Дослідимо |
||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
спочатку прямий згин балки |
|||||||
y |
|
F |
q |
M |
|
|
|
сталого |
|
поперечного |
перері- |
|||||
|
|
|
|
зу, |
що |
має принаймі одну |
||||||||||
x |
|
|
|
|
|
|
|
б) |
вісь |
симетрії. |
Вісь x |
прямо- |
||||
|
|
|
|
|
|
|
|
кутної |
|
системи |
|
координат |
||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
сумістимо з віссю балки, а |
|||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
осі y, z - з головними центра- |
|||||||
|
|
|
рис. 7.1. |
|
|
|
|
льними осями її поперечного |
||||||||
|
|
|
|
|
|
|
перерізу, |
причому |
будемо |
|||||||
|
|
|
|
|
|
|
|
|
||||||||
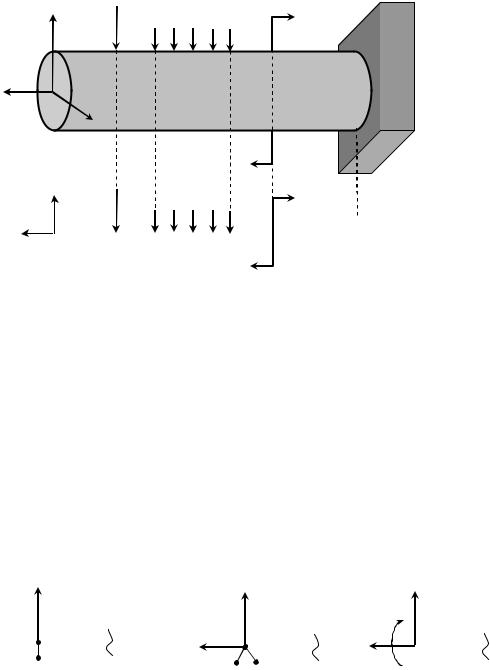
вважати, що вертикальна вісь y є віссю симетрії перерізу(рис.7.1а). Будемо вважати, що прикладене до балки навантаження лежить в площині симетріїOxy. Очевидно, що зігнута вісь балки буде лежати в цій же площині.
На розрахунковій схемі балку зображують у вигляді її осі(рис.7.1б). При цьому силова площина Oxy співпадає з площиною рисунка.
Для того щоб забезпечити нерухомість балки, при дії на неї навантаження, її слід закріпити. Конструктивні форми опор різноманітні. При розрахунку їх схематизують і представляють у вигляді трьох типів опор :
1)шарнірно-рухома опора (рис.7.2а), в якій виникає тільки одна складова реакції - Ra , що направлена вздовж опорного стержня.
2)шарнірно-нерухома опора (рис.7.2б), в якій дві складові Ra і H a .
3)жорстке защемлення (рис.7.2в), де виникають три складові – вертикальна Ra , гори-
|
RA |
|
RA |
M A |
|
RA |
|||
|
|
|
H A |
|
|
|
|
|
|
A |
|
|
|
A |
H A |
|
A |
||
|
|
|
|
|
|
|
|
в) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a) |
|
б) |
|
|
|||
рис. 7.2.
зонтальна H a , опорний момент
M a .
Для плоскої системи сил можна скласти три незалежних рівняння статики для визначення невідомих
реакцій.
Коли закріплення балки таке, що реакції в опорах можна визначити з рівнянь статики, балку називають статично визначною, а якщо реакцій більше ніж рівнянь статики – статично невизначною.
- 39 -
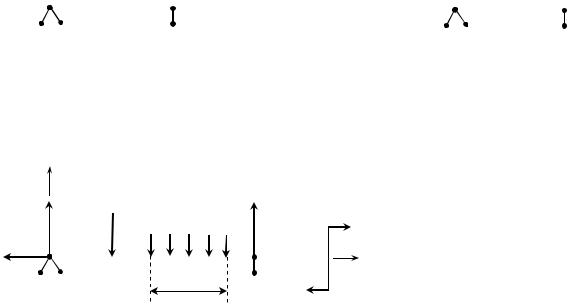
Найпростіші статично визначні балки:
а) балка, кінці якої на опорах (рис.7.3а). Це – проста балка б) балка з одним защемленим і другим вільним краєм (рис.7.3б). Це – консоль.
в) балка на двох опорах, що має одну або дві консолі(рис.7.3в). Таку балку називають консольною балкою.
|
|
A |
|
|
|
|
|
B |
|
|
A |
|
|
|
|
|
A |
|
B |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
б) |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
a) |
|
|
|
|
|
|
|
|
|
|
|
|
|
в) |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рис. 7.3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Відстань між опорами балки або довжину консолі називаютьпрольотом. Бувають одно- |
|||||||||||||||||||||||||
прольотні, двопрольотні і інші балки. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
Навантаження на балку складають наступні сили (рис.7.4): зосереджені сили F [кН], па- |
|||||||||||||||||||||||||
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
ри сил з моментом M [кНм], розподіле- |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
не по довжині навантаження з інтен- |
|||||||||
|
|
|
|
|
RA |
F |
|
q |
RB |
|
M |
сивністю q [кН/м]. Будемо вважати, що |
||||||||||||||||
|
H A |
|
|
|
|
|
|
|
|
|
x |
навантаження q розподілене по довжи- |
||||||||||||||||
|
|
|
|
A |
|
|
|
|
|
|
|
|
B |
|
ні рівномірно (q=const). Якщо до балки |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
прикладене розподілене навантаження, |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
то повинна бути вказана довжина, на |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
якій воно діє. Навантаження F і q вва- |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
жатимемо перпендикулярним |
|
до осі |
|||||||
|
|
|
|
|
|
|
|
|
рис. 7.4. |
|
|
|
|
балки. |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для визначення |
опорних |
реакцій в |
|||||||
|
|
|
опорах балки складають рівняння статики (рис.7.4): |
|
|
|
|
|
||||||||||||||||||||
а) |
сума проекцій всіх сил на вісьx балки ( åX =0 ) ; звідки визначають H A . В випадку, коли |
|||||||||||||||||||||||||||
|
навантаження на балку перпендикулярне до осі балки, одержуємо H A =0 ; |
|
|
|||||||||||||||||||||||||
б) |
сума моментів всіх сил відносно опорного шарніруA рівна нулю åM A =0 . Звідки знахо- |
|||||||||||||||||||||||||||
|
дять величину RB ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
в) |
сума моментів всіх сил відносно опорного шарніраB åM B =0 . Звідки знаходять величи- |
|||||||||||||||||||||||||||
|
ну RA . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Якщо реакції RA |
i RB визначені, то слід перевірити чи вони визначені правильно. Для |
||||||||||||||||||||||||
цього використовують рівняння åY = 0 .
7.2. Поперечна сила Q(x) і згинальний момент M(x).
Під дією зовнішніх сил в перерізах балки, як протидія їм, виникають внутрішні сили. Для з’ясування характеру цих сил і визначення їх величин використовують метод перерізів. Встановлено, що цими внутрішніми силами єзгинальний момент M(x) і поперечна сила Q(x) (рис.7.5), для визначення яких можна сформулювати наступні правила:
·Поперечна сила Q(x) в довільному перерізі балки чисельно дорівнює алгебраїчній сумі проекцій на вертикальну вісьy зовнішніх сил, що знаходяться з однієї сторони(зліва або справа) від даного перерізу. Додатнім при цьому вважаються ліві сили, які напрямлені вгору, або праві – які напрямлені вниз.
-40 -
