Добавил:

posterp Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Днепропетровский национальный университет железнодорожного транспорта им. академика В. Лазаряна

Предмет:

Высшая математика

Файл:

Частина 1

.pdf

Скачиваний:

Добавлен:

26.04.2021

Размер:

967.56 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 138 9 10 11 12 13 > Следующая >>>

																																								“Курс вищої математики. Частина 1.”
(a			−		λ	2	)m		2	+ a n				2		= 0		− m		2		+ 3n					2		= 0																		1
	11					2			2			12		2						2							2							вважаючи m2 = 1, отримаємо n2 =													1
	a m				+ (a					−λ			)n			= 0																		вважаючи m2 = 1, отримаємо n2 =													3
	a m			2	+ (a			22		−λ		2	)n		2	= 0			3m2				−3n2 = 0																								3
	12			2				22				2			2				3m2				−3n2 = 0
Власні вектори:
																	u = 1+3 = 2;																	u	2		= 1+ 1 = 2
																		1																	2					3				3
																																								3				3
Знаходимо координати одиничних векторів нового базису.
																			e′ =				1	;−				3							e′					3	;	1
																			e′ =					;−											e′			=			;
																			1				2				2									2				2		2
																							2				2													2		2
Маємо наступне рівняння лінії в новій системі координат:
																											′		2	+				′			2	= 6
																							2(x )							+		6( y )						= 6
Канонічне рівняння лінії в новій системі координат матиме вигляд:
																											′		2					′		2
																								(x )						+		( y )						=1
																								(		3)2				+				12				=1
																															2
																														1.5
																															1
																														0.5
													-2						-1																						1				2
																													-0.5
																														-1
																													-1.5
																														-2
					Приклад. Використовуючи теорію квадратичних форм, привести до канонічного
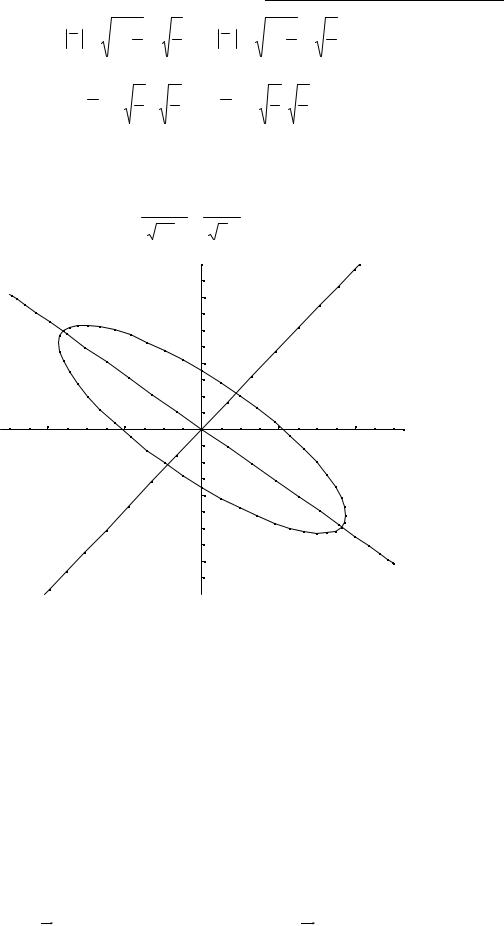
вигляду рівняння лінії другого порядку. Схемний зобразити графік.
																			5x2 + 4 6xy + 7 y2 − 22 = 0
					Рішення:									Складемо								характеристичне																		рівняння					квадратичної	форми
5x2		+ 4				6xy + 7 y2 : при a												= 5, a					= 2				6, a				22			= 7.
																11					12										22
a11 −λ								a12				=		5 −λ				2 6			= 35 −7λ									−5λ + λ								2	− 24		= λ		2	−12λ +11 = 0
	a12					a22 −					λ	=		2 6 7 −λ							= 35 −7λ									−5λ + λ									− 24		= λ			−12λ +11 = 0
	a12					a22 −					λ			2 6 7 −λ
Вирішивши це рівняння, отримаємо λ1 = 1, λ2 = 11.
Знайдемо координати власних векторів:
(a			−		λ	1	)m			+ a n					= 0		2m +						6n			= 0																					2
	11					1		1			12		1						1					1									вважаючи m1 = 1, отримаємо n1 = −														2
					+ (a22 −λ 1 )n1 = 0																												вважаючи m1 = 1, отримаємо n1 = −
a12 m1					+ (a22 −λ 1 )n1 = 0														6m		+3n					= 0																					6
(a							)m													1				1
(a			−		λ	2	)m		2	+ a n				2		= 0		−3m				2	+		6n			2		= 0																	3
	11					2			2			12		2								2						2							вважаючи m2 = 1, отримаємо n2 =												3
	a m				+ (a					−λ			)n			= 0																			вважаючи m2 = 1, отримаємо n2 =												6
	a m			2	+ (a			22		−λ		2	)n		2	= 0			6m2				− 2n2 =							0																	6
	12			2				22				2			2				6m2				− 2n2 =							0
Власні вектори:

										“Курс вищої математики. Частина 1.”
u =	1+ 2 = 5 ;					u	2		= 1+ 3			= 5
1		3			3		2				2		2
		3			3						2		2
Знаходимо координати одиничних векторів нового базису.
		3	;−	2		e′				2	;	3
e′ =			;−			e′			=		;
1		5		5		2				5		5
		5		5						5		5
Маємо наступне рівняння лінії в новій системі координат:
			′ 2			′ 2		= 22
		(x )			+11( y )			= 22
Канонічне рівняння лінії в новій системі координат матиме вигляд:
			′		2	′		2
			(x )			( y )
		( 22 )2				+ ( 2)2			=1
						4
						2
-4	-2									2			4
						-2
						-4
Приклад. Використовуючи теорію квадратичних форм, привести до канонічного
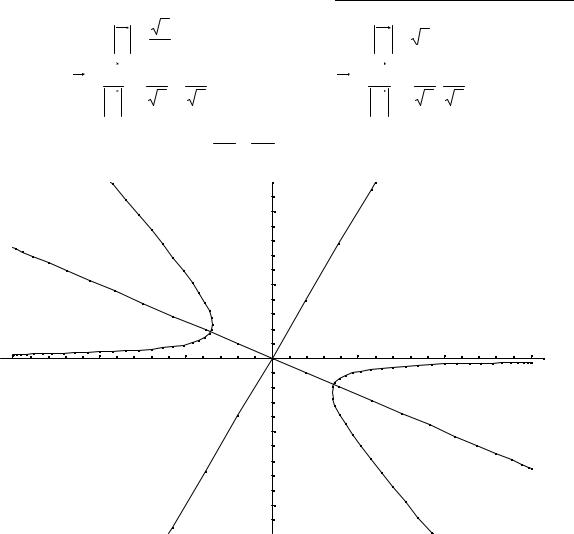
вигляду рівняння лінії другого порядку. Схемний зобразити графік.
		4ху + 3у2 + 16 = 0

Коефіцієнти: a11 = 0;

a12 = 2;

a22 = 3.

Характеристичне рівняння:

0 −λ

= −3λ + λ2

− 4 = 0

3 −

Коріння: λ1 = -1, λ2 = 4.

Для λ1 = -1

Для 2 = 4

1 m

+ 2n = 0

− 4m

= 0

2m1

+ 4n1 = 0

2m2

− n2 = 0

m1 = 1;

n1 = -0,5;

m2 = 1;

n2 = 2;

u1 = (1; -0,5)

u2 = (1; 2)

														“Курс вищої математики. Частина 1.”
		u	1	=	5									u	2	=	5
			1		2										2
					2
e1′ = u1 = (					2	;−	1	)						e2′ = u2 = (			1	;	2 )
		u1			5		5							u2			5		5
Отримуємо: − x	′2	+ 4y	′2	= −16;				x	′2	−	y	′2	=1	-каноническое рівняння гіперболи.
Отримуємо: − x		+ 4y		= −16;				16		−	4		=1	-каноническое рівняння гіперболи.
											10
											5
-15		-10				-5								5				10	15
											-5
											-10
					Введення в математичний аналіз.

Числова послідовність.

Визначення. Якщо кожному натуральному числу n поставлено у відповідність число хn, то говорять, що задана послідовність

x1, х2 ., хn = {xn}

Загальний елемент послідовності є функцією від n. xn = f(n)

Таким чином послідовність може розглядатися як функція.

Задати послідовність можна різними способами – головне, щоб був вказаний спосіб отримання будь-якого члена послідовності.

Приклад. {xn} = {(-1)n} або {xn} = -1; 1; -1; 1; . {xn} = {sinn/2} або {xn} = 1; 0; 1; 0; .

Для послідовностей можна визначити наступні операції:

1) Множення послідовності на число m: m{xn}= {mxn}, тобто mx1, mx2 .

					“Курс вищої математики. Частина 1.”
2)	Складання (віднімання) послідовностей: {xn} ± {yn} = {xn ± yn}.
3)	Твір послідовностей: {xn} {yn} = {xnyn}.
4)	Приватне послідовностей: {xn }		xn	при {yn} ≠ 0.
		=	xn
		=
	{yn }	yn

Обмежені і необмежені послідовності.

Визначення. Послідовність {xn} називається обмеженою, якщо існує таке число М>0, що для будь-якого n вірна нерівність:

xn < M

тобто всі члени послідовності належать проміжку (-М; M).

Визначення. Послідовність {xn}називається обмеженою зверху, якщо для будьякого n існує таке число М, що

xn ≤ M.

Визначення. Послідовність {xn}називається обмеженою знизу, якщо для будьякого n існує таке число М, що

xn ≥ M

Приклад. {xn} = n – обмежена знизу {1, 2, 3 . }.

Визначення. Число а називається межею послідовності {xn}, якщо для будьякого позитивного >ε0 існує такий номер N, що для всіх n > N виконується умова:

a −xn < ε.

Це записується: lim xn = а.

В цьому випадку говорять, що послідовність {xn}сходиться до а при n→∞.

Властивість: Якщо відкинути какоеабо число членів послідовності, то виходять нові послідовності, при цьому якщо сходиться одна з них, то сходиться і інша.

Приклад. Довести, що межа послідовності lim (−n1)n = 0 .

Хай при n > N вірно	0	−	(−1)n	< ε , тобто	1	< ε . Це вірно приn >	1	, таким чином, якщо
			n		n		ε

за N узяти цілу частина відε1 , то твердження, приведене вище, виконується.

Приклад. Показати, що при n послідовність 3, 2 12 , 2 13 , 2 14 ,..., 2 + 1n має межею число 2.

“Курс вищої математики. Частина 1.”

Разом: {xn}= 2 + 1/n; 1/n = xn – 2

Очевидно, що існує таке число n, що xn − 2 = 1n < ε , тобто lim {xn} = 2.

Теорема. Послідовність не може мати більш за одну межу.

Доказ. Припустимо, що послідовність {xn}має дві межі а і b, не рівні один одному.

xn → а; xn → b; а ≠ b.

Тоді за визначенням існує таке число ε >0, що

a − xn

b − xn

Запишемо вираз:

a −b

(a − xn ) + (xn −b)

≤

a − xn

xn −b

= ε

А оскільки ε- будь-яке число, то a −b = 0 , тобто а = b. Теорема доведена.

Теорема. Якщо xn→ → а, те xn → a .

Доказ. З xn→ → а витікає, що xn − a < ε . В той же час:

xn − a ≤ xn − a тобто xn − a < ε , тобто xn → a . Теорема доведена.

Теорема. Якщо xn→ → а, те послідовність {xn} обмежена.

Слід зазначити, що зворотне твердження невірне, тобто з обмеженості послідовності не виходить її збіжність.

		+	1		, при четном n
	1
	1		n
	Наприклад, последовательностьне xn =		n		має межі, хоча
		−	1		, при нечетном n
	2	−		n	, при нечетном n
				n
xn	≤ 2.
xn	≤ 2.

Монотонні послідовності.

Визначення. 1) Якщо xn+1 > xn для всіх n, то послідовність зростає. 2)Если xn+1 ≥ xn для всіх n, то послідовність неубутна.

3)Если xn+1 < xn для всіх n, то послідовність убуває.

4)Если xn+1 ≤ xn для всіх n, то послідовність не зростає

Всі ці послідовності називаються монотонними. Зростаючі і убуваючі послідовності називаються строго монотонними.

“Курс вищої математики. Частина 1.”

Приклад. {xn} = 1/n – що убуває і обмежена {xn} = n – що зростає і необмежена.

Приклад. Довести, що послідовність {xn}=

що монотонна зростає.

2n +1

Знайдемо член послідовності {xn+1}=

n +1

2n + 2 +

2n +3

Знайдемо знак різниці: {xn}-{xn+1}=

−

n +1

2n2 +3n − 2n2 − 2n − n −1

2n +1

2n +3

(2n +1)(2n +3)

−1

< 0 оскільки nN, то знаменник позитивний при будь-якому n.

(2n +1)(2n +3)

Таким чином, xn+1 > xn. Послідовність зростає, що і слід було довести.

Приклад. З'ясувати є такою, що зростає або убуває послідовність

{xn} = 5nn .

Знайдемо	xn+1	=	n +1	.	Знайдемо різницю xn+1 − xn =	n +1	−	n	=	n +1−5n	=
						5 5n		5n		5 5n
			5n+1

= 15−54nn оскільки nN, то 1 – 4n <0, тобто хn+1 < xn. Послідовність монотонно убуває.

Слід зазначити, що монотонні послідовності обмежені принаймні з одного боку.

Теорема. Монотонна обмежена послідовність має межу.

Доказ. Розглянемо монотонну неубутну послідовність

х1 ≤ х2 ≤ х3 . хn xn+1 ≤ .

Ця послідовність обмежена зверху: xn ≤ M, де М – деяке число.

Оскільки будь-яке, обмежене зверху, числова множина має чітку верхню грань, то для будь-якого >ε0 існує таке число N, що xN > а -, де а – деяка верхня грань множини.

Оскільки {xn}- неубутна послідовність, то при N > n а - ε < xN ≤ xn xn > а - ε.

Звідси а - ε < xn < а + ε

-ε < xn – а < ε або xn - а, тобто lim xn = а.

Для решти монотонних послідовностей доказ аналогічний. Теорема доведена.

Число е.

“Курс вищої математики. Частина 1.”

Розглянемо послідовність {xn} = 1

Якщо послідовність {xn} монотонна і обмежена, то вона має кінцеву межу.

По формулі бінома Ньютона:

n(n

−1)

n(n −1)(n

− 2) 1

n(n −1)(n − 2)...[n −

(n −1)] 1

=1+

... +

1 2 3

1 2 3 n

або, що те ж саме

k −1

n −1

+1+

−

+... +

−

1−

... 1−

+...

−

1−

... 1−

Покажемо, що послідовність {xn} – що зростає. Дійсно, запишемо вираз xn+1 і

порівняємо його з виразом xn:

k −1

xn+1 =

+... +

−

1+1+

1−

+... +

1−

... 1−

...

n +1

n −1

... 1

−

1−

... 1−

n +1

n +

+1)!

n +1

Кожен доданок у виразі xn+1 більше відповідного значення xn, і, крім того, у xn+1 додається ще один позитивний доданок. Таким чином, послідовність {xn} зростає.

Доведемо тепер, що при будь-якому n її члени не перевершують три: xn < 3.

1−

<1+

xn <1

+1+

+... +

+1+

+... +

=1+

= 3

2n+1

2! 3!

1−

геометр. прогрессия

Отже,

послідовність

- що монотонно зростає і обмежена зверху, тобто має

кінцеву межу. Цю межу прийнято позначати буквою е.

		1	n
lim 1	+			= e
		n
n→∞

1 n

З нерівності 1+

< 3 виходить, що е ≤ 3. Відкидаючи в рівності для {xn} всі члени,

починаючи з четвертого, маємо:

> 2 +

−

переходячи до межі, отримуємо

e ≥ 2 +

= 2,5

Таким чином, число е поміщене між числами 2,5 і 3. Якщо узяти більшу

кількість членів ряду, то можна отримати точнішу оцінку значення числа е.

Можна показати, що число е ірраціональне і його значення рівне 2,71828.

1 x

Аналогічно можна показати, щоlim 1+

= e ,

розширивши вимоги до х до будь-

x→∞

якого дійсного числа: Припустимо:

“Курс вищої математики. Частина 1.”

≥

n +1

≥1+

1 n+1

1 x

n +1

1 n+1

1 n

1 x

Знайдемо lim 1

= e 1 = e;

lim 1

= e;

lim 1

= e

n→∞

x→∞

Число е є підставою натурального логарифма.

e y

loge x = ln x = y,

т.е.

= x.

Вище представлений графік функції у = lnx.

Зв'язок натурального і десяткового логарифмів.

Хай х = 10у, тоді lnx = ln10y, отже lnx = yln10

у = lg x = lnln10x = M ln x; ln x = M1 lg x , де М = 1/ln10 ≈ 0,43429.- модуль переходу.

Межа функції в точці.

уf(x)

A + ε

A - ε

0	а - ∆ а а + ∆ x

Хай функція f(x) визначена в деякій околиці точки х = а (тобто в самій точці х = а функція може бути і не визначена)

Визначення. Число А називається межею функції f(x) при ха→, якщо для будьякого >ε0 існує таке число >∆0, що для всіх х таких, що

	0 < x - а < ∆
вірна нерівність	f(x) - A< ε.

Те ж визначення може бути записане в іншому вигляді: Якщо а - ∆ < x < а +∆, x ≠ а, те вірне нерівність А - ε < f(x)< A + .

“Курс вищої математики. Частина 1.”

Запис межі функції в точці: lim f (x) = A

x→a

Визначення. Якщо f(x) → A1 при х → а тільки при x < а, те lim f (x) = A1 -

x→a−0

називається межею функції f(x) в точці х = а зліва, а якщо f(x) → A2 при х а тільки при

x > а, те lim f (x) = A2 називається межею функції f(x) в точці х = а справа.

x→a+0

f(x)

А2

А1

Приведене вище визначення відноситься до випадку, коли функція f(x) не визначена в самій точці х = а, але визначена в деякій скільки завгодно малій околиці цієї крапки.

Межі А1 і А2 називаються також односторонніми межами функції f(x) в точці х = а. Також говорять, що А – кінцева межа функції f(x).

Межа функції при прагненні аргументу до нескінченності.

Визначення. Число А називається межею функції f(x) при х→∞, якщо для будьякого числа >ε0 існує таке число М>0, що для всіх х, х>M виконується нерівність

A − f (x) < ε

При цьому передбачається, що функція f(x) визначена в околиці нескінченності.

Записують: lim f (x) = A.

x→∞

Графічно можна представити:

уу

A A

0	0
x	x

“Курс вищої математики. Частина 1.”

уу

A A

0		0
x x
Аналогічно можна визначити межі	lim	f (x) = A для будь-якого х>M і
	x→+∞
lim f (x) = A для будь-якого х<M.
x→−∞

Основні теореми про межі.

Теорема 1. limC = C , де З = const.

x→a

Наступні теореми справедливі при припущенні, що функції f(x) і g(x) мають кінцеві межі при ха.→

Теорема 2. lim( f (x) ± g(x)) = lim f (x) ± lim g(x)
x→a	x→a	x→a

Доведення цієї теореми буде приведено нижче.

Теорема 3. lim[ f (x) g(x)] = lim f (x) lim g(x)
x→a	x→a	x→a
Слідство. limC f (x) = C lim f (x)
x→a	x→a

Теорема 4. lim	f (x)		lim f (x)
	f (x)	=	x→a
	g(x)	=	lim g(x)
x→a	g(x)		lim g(x)
			x→a

при lim g(x) ≠ 0

x→a

Теорема 5. Якщо f(x) >0 поблизу точки х = а і, то А>0.

Аналогічно визначається знак межі при f(x)< 0, f(x) ≥ 0, f(x) ≤ 0.

Теорема 6. Якщо g(x) ≤ f(x) ≤ u(x) поблизу точки х = а і, то і lim = A.

x→a

Визначення. Функція f(x) називається обмеженої поблизу точки х = а, якщо існує таке число М>0, що f(x)<M поблизу точки х = а.

Теорема 7. Якщо функція f(x) має кінцеву межу при ха, то вона обмежена поблизу точки х = а.

Доказ. Хайlim f (x) = A , тобто f (x) − A < ε , тоді

x→a

<<< < Предыдущая 1 2 3 4 5 6 78 / 138 9 10 11 12 13 > Следующая >>>

Соседние файлы в предмете Высшая математика

#
03.05.2021776.15 Кб3490.pdf
#
03.05.20211.59 Mб5683.pdf
#
26.04.20211.64 Mб3M-008.pdf
#
26.04.20211.23 Mб3M-040.pdf
#
26.04.2021439.24 Кб5M-051.pdf
#
26.04.2021967.56 Кб12Частина 1.pdf
#
26.04.2021882.81 Кб2Частина 2.pdf
#
26.04.20211.01 Mб2Частина 3.pdf
#
26.04.2021669.46 Кб6Частина 4.pdf