Частина 1

“Курс вищої математики. Частина 1.”

х0

Визначення. Точка х0 називається точкою розриву функції f(x), якщо f(x) не визначена в точці х0 або не є безперервною в цій точці.

Визначення. Точка х0 називається точкою розриву 1- го роду, якщо в цій точці функція f(x) має кінцеві, але не рівні один одному ліва і права межі.

lim f (x) ≠ lim f (x)

Для виконання умов цього визначення не потрібний, щоб функція була визначена в точці х = х0, достатньо того, що вона визначена зліва і праворуч від неї.

З визначення можна зробити вивід, що в точці розриву 1 – го роду функція може мати тільки кінцевий стрибок. У деяких окремих випадках точку розриву 1 – го роду ще іноді називають усуненою точкою розриву, але докладніше про це поговоримо нижче.

Визначення. Точка х0 називається точкою розриву 2 – го роду, якщо в цій точці функція f(x) не має хоч би однієї з односторонніх меж або хоч би один з них нескінченний.

Приклад. Функція Дирихле (Дирихле Петер Густав(1805-1859) – німецький математик, членкореспондент Петербурзькою АН 1837г)

7.5

5

2.5

-2.5

-5

-7.5

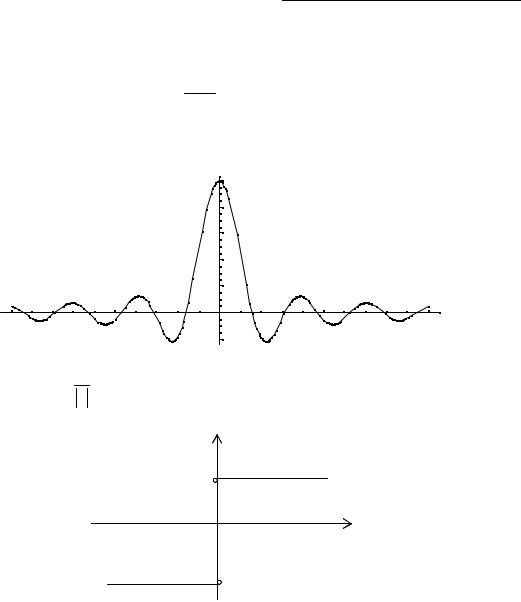
Приклад. f(x)=

91

Таким чином, для того, щоб точка розриву 1 – го роду була усуненою, необхідно, щоб односторонні межі справа і зліва були кінцеві і рівні, а функція була б в цій точці не визначена.

Безперервність функції на інтервалі і на відрізку.

Визначення. Функція f(x) називається безперервною на інтервалі (відрізку),

якщо вона безперервна в будь-якій точці інтервалу (відрізання).

92

“Курс вищої математики. Частина 1.”

При цьому не потрібна безперервність функції на кінцях відрізання або інтервалу, необхідна тільки одностороння безперервність на кінцях відрізання або інтервалу.

Властивості функцій, безперервних на відрізку.

Властивість 1: (Перша теорема Вейерштраса (Вейерштрас Карл (1815-1897) - німецький математик)). Функція, безперервна на відрізку, обмежена на цьому відрізку, тобто на відрізку [а, b] виконується умова –M ≤ f(x) ≤ M.

Доказ цієї властивості заснований на тому, що функція, безперервна в точці х0, обмежена в деякій її околиці, а якщо розбивати відрізок [а, b] на нескінченну кількість відрізань, які “стягуються” до точки х0, то утворюється деяка околиця точки х0.

Властивість 2: Функція, безперервна на відрізку [а, b], приймає на нім найбільше і найменше значення.

Тобто існують такі значення х1 і х2, що f(x1)= m, f(x2)= M, причому m ≤ f(x) ≤ M

Відзначимо ці найбільші і найменші значення функція може приймати на відрізку і кілька разів (наприклад – f(x)= sinx).

Різниця між найбільшим і найменшим значенням функції на відрізку називається коливанням функції на відрізку.

Властивість 3: (Друга теорема Больцано – Коші). Функція, безперервна на відрізку [а, b], приймає на цьому відрізку всі значення між двома довільними величинами.

Властивість 4: Якщо функція f(x) безперервна в точці х = х0, то існує деяка околиця точки х0, в якій функція зберігає знак.

Властивість 5: (Перша теорема Больцано (1781-1848) – Коші). Якщо функція f(x) - безперервна на відрізку [а, b] і має на кінцях відрізання значення протилежних знаків, то існує така точка усередині цього відрізання, де f(x)= 0.

Тобто, якщо sign(f(a)) ≠ sign(f(b)), то х0: f(x0) = 0.

Визначення. Функція f(x) називається рівномірно безперервною на відрізку [а, b], якщо для будь-якого >0 існує >0 таке, що для будь-яких точок х1 [а,b] і x2 [а,b] таких, що

Відмінність рівномірної безперервності від “звичайної” в тому, що для будьякого ε існує своє, не залежне від х, а при “звичайній” безперервності ∆ залежить від ε ї х.

Властивість 6: Теорема Кантора (Кантор Георг (1845-1918) - німецький математик). Функція, безперервна на відрізку, рівномірно безперервна на нім.

(Ця властивість справедлива тільки для відрізань, а не для інтервалів і напівінтервалів.)

93

Властивість 7: Якщо функція f(x) визначена, монотонна і безперервна на деякому проміжку, то і зворотна нею функція х = g(y) теж однозначна, монотонна і безперервна.

Приклад. Досліджувати на безперервність функцію і визначити тип точок розриву, якщо вони є.

у

3

2

Приклад. Досліджувати на безперервність функцію і визначити тип точок розриву, якщо вони є.

94

2

1

Комплексні числа.

Визначення. Комплексним числом z називається вираз, де а і b – дійсні числа, i – уявна одиниця, яка визначається співвідношенням:

При цьому число а називається дійсною частиною числа z (а = Re z), а b-

уявною частиною (b = Im z).

Якщо а =Re z =0, те число z буде чисто уявним, якщо b = Im z = 0, те число z буде дійсним.

рівними, якщо відповідно рівні їх дійсні і уявні частини:

Визначення. Комплексне число рівне нулю, якщо відповідно рівні нулю дійсна і уявна частини.

a = b = 0.

Поняття комплексного числа має геометричне тлумачення. Безліч комплексних чисел є розширенням безлічі дійсних чисел за рахунок включення безлічі уявних чисел. Комплексні числа включають всю безліч чисел, які вивчалися раніше. Так натуральні, цілі, раціональні, ірраціональні, дійсні числа є, взагалі кажучи, окремими випадками комплексних чисел.

95

“Курс вищої математики. Частина 1.”

Якщо будь-яке дійсне число може бути геометрично представлене у вигляді крапки на числовій прямій, то комплексне число представляється крапкою на площині, координатами якої будуть відповідно дійсна і уявна частини комплексного числа. При цьому горизонтальна вісь буде дійсною числовою віссю, а вертикальна - уявною віссю.

у

A(а, b)

r b

ϕ

Таким чином, на осі ОХ розташовуються дійсні числа, а на осі Оy – чисто уявні. За допомогою подібного геометричного уявлення можна представляти числа в

так званій тригонометричній формі.

Тригонометрична форма числа.

З геометричних міркувань видно, що a = r cos ϕ; b = r sin ϕ. Тоді комплексне число можна представити у вигляді:

z = a +ib = r cos ϕ+ir sin ϕ = r(cos ϕ+i sin ϕ)

Така форма запису називається тригонометричною формою запису

комплексного числа.

При цьому величина r називається модулем комплексного числа, а кут нахилу ϕ - аргументом комплексного числа.

Очевидно, що комплексно – зв'язані числа мають однакові модулі і протилежні аргументи.

z = z ; Arg z = −Arg z.

Дії з комплексними числами.

Основні дії з комплексними числами витікають з дій з многочленами.

1) Складання і віднімання.

z = z1 ± z2 = (a1 + ib1 ) ± (a2 + ib2 ) = (a1 ± a2 ) + i(b1 ± b2 )

96

“Курс вищої математики. Частина 1.”

z = (a1 ± a2 )2 + (b1 ± b2 )2

2) Множення.

z = z1 z2 = (a1 +ib1 )(a2 +ib2 ) = a1a2 +ia1b2 +ib1a2 +i2b1b2

z= z1 z2 = (a1a2 −b1b2 ) +i(a1b2 + b1a2 )

Утригонометричній формі:

4)Піднесення до ступеня.

Зоперації множення комплексних чисел виходить, що

z 2 = zz = r 2 (cos 2ϕ+i sin 2ϕ)

У загальному випадку отримаємо:

z n = r n (cos nϕ+i sin nϕ) ,

де n – ціле позитивне число.

Цей вираз називається формулою Муавра.

(Абрам де Муавр (1667 – 1754) – англійський математик)

Формулу Муавра можна використовувати для знаходження тригонометричних функцій подвійного, потрійного і так далі кутів.

Приклад. Знайти формули sin2 і cos2ϕ.

97

“Курс вищої математики. Частина 1.”

Розглянемо деяке комплексне число

Тоді з одного боку z 2 = r 2 (cos2 ϕ+ 2i cos ϕsin ϕ−sin 2 ϕ) .

По формулі Муавра: Прирівнюючи, отримаємо

Оскільки два комплексні числа рівні, якщо рівні їх дійсні і уявні частини, то

Таким чином, корінь n – ой ступені з комплексного числа має n різних значень.

Показова форма комплексного числа.

Розглянемо показову функцію

Можна показати, що функція w може бути записана у вигляді:

w = ex+iy = ex (cos y +i sin y)

Дана рівність називається рівнянням Ейлера. Виведення цього рівняння буде розглянуто пізніше. (Див. ).

Для комплексних чисел будуть справедливі наступні властивості:

Якщо в рівнянні Ейлера показник ступеня прийняти за чисто уявне число (х=0), то отримуємо:

eiy = cos y +i sin y

Для комплексно – зв'язаного числа отримуємо: e−iy = cos y −i sin y

З цих двох рівнянь отримуємо:

98

“Курс вищої математики. Частина 1.”

Цими формулами користуються для знаходження значень ступенів тригонометричних функцій через функції кратних кутів.

Якщо представити комплексне число в тригонометричній формі:

z= r(cos ϕ+i sin ϕ)

іскористаємося формулою Ейлера:

z = reiϕ

Отримана рівність і є показова форма комплексного числа.

Розкладання многочлена на множники._

раціональною функцією від х.

Теорема Безу. (Етьенн Безу (1730 – 1783) – французький математик)

При діленні многочлена f(x) на різницю x – а виходить залишок, рівний f(a).

Доказ. При діленні многочлена f(x) на різницю x – а приватним буде многочлен f1(x) ступеня на одиницю меншою, ніж f(x), а залишком – постійне число R.

f (x) = f1 (x)(x − a) + R

Переходячи до межі при х → а, отримуємо f(a)= R.

Слідство. Якщо, а – корінь многочлена, тобто f(a)= 0, то многочлен f(x) ділиться на (х – а) без залишку.

Визначення. Якщо рівняння має вид Р(х) = 0, де Р(х) – многочлен ступеня n, то це рівняння називається рівнянням алгебри ступеня n.

Теорема. (Основна теорема алгебри) Всяка ціла раціональна функція f(x) має, принаймні, один корінь, дійсний або комплексний.

Теорема. Всякий многочлен n – ой ступеню розкладається на n лінійних множників вигляду (x – а) і множнику, рівному коефіцієнту при xn.

Теорема. Якщо два многочлени тотожно рівні один одному, то коефіцієнти одного многочлена рівні відповідним коефіцієнтам іншого.

Якщо серед коріння многочлена зустрічається кратне коріння, то розкладання на множники має вигляд:

f (x) = A0 (x − a1 )k1 (x − a2 )k2 ...(x − am )km . k1 + k2 +... + km = n

99

“Курс вищої математики. Частина 1.”

ki - кратність відповідного кореня.

Звідси витікає, що будь-який многочлен n – ой ступені має рівно n коріння (дійсних або комплексних).

Цю властивість має велике значення для вирішення рівнянь алгебри, диференціальних рівнянь і грає важливу роль в аналізі функцій.

Розглянемо декілька прикладів дій з комплексними числами.

a) Очевидно, справедливо наступне перетворення:

Далі проводимо ділення двох комплексних чисел:

Набуваємо значення заданого виразу: 16(-i)4 = 16i4 =16.

б) Число z = 2 − 2 3i представимо у вигляді, де

Тоді z = 4(cos 600 −i sin 600 ) .

Для знаходження z 20 воспльзуемся формулою Муавра.

z 20 = 420 (cos12000 −i sin12000 ) = 420 (cos(3 2π+1200 ) −i sin(3 2π+1200 )) =

Якщо, то

100