Частина 1

Кут між площинами.

N2

ϕ1 ϕ 0

N1

Кут між двома площинами в просторі ϕ пов'язаний з кутом між нормалями до цих площин 1 співвідношенням: = ϕ1 або ϕ = 1800 - 1, тобто

cosϕ = ±cos1.

Визначимо кут ϕ1. Відомо, що площини можуть бути задані співвідношеннями:

N1 (A1, B1, C1), N2 (A2, B2, C2). Кут між векторами нормалі знайдемо з їх скалярного твору:

cosϕ1 = N1 N2 .

N1 N2

Таким чином, кут між площинами знаходиться по формулі:

51

“Курс вищої математики. Частина 1.”

Вибір знаку косинуса залежить від того, який кут між площинами слід знайти – гострий, або суміжний з ним тупий.

Умови паралельності і перпендикулярності площин.

На основі отриманої вище формули для знаходження кута між площинами можна знайти умови паралельності і перпендикулярності площин.

Для того, щоб площини були перпендикулярні необхідно і достатньо, щоб косинус кута між площинами дорівнював нулю. Ця умова виконується, якщо:

A1 A2 + B1 B2 +C1C2 = 0 .

Площини паралельні, вектори нормалей коллинеарны: N1 N2 .Это умова

виконується, якщо: A1 = B1 = C1 .

A2 B2 C2

Кут між прямими в просторі.

Хай в просторі задані дві прямі. Їх параметричні рівняння: l1: rr = r1 + S1t

l2: rr = r2 + S2t

rr = (x, y, z); r1 = (x1 , y1 , z1 ); r2 = (x2 , y2 , z2 ); S1 = (m1 , n1 , p1 ); S2 = (m2 , n2 , p2 ).

Кут між прямими ϕ і кут між направляючими векторами цих прямих зв'язані співвідношенням: ϕ = ϕ1 або ϕ = 1800 - ϕ1. Кут між направляючими векторами знаходиться з скалярного твору. Таким чином:

Умови паралельності і перпендикулярності прямих в просторі.

Щоб дві прямі були паралельні необхідно і достатньо, щоб направляючі вектори цих прямих були коллинеарны, тобто їх відповідні координати були пропорційні.

m1 = n1 = p1 m2 n2 p2

Щоб дві прямі були перпендикулярні необхідно і достатньо, щоб направляючі вектори цих прямих були перпендикулярні, тобто косинус кута між ними рівний нулю.

m1m2 + n1n2 + p1 p2 = 0

52

“Курс вищої математики. Частина 1.”

Кут між прямою і площиною.

Визначення. Кутом між прямою і площиною називається будь-який кут між прямою і її проекцією на цю площину.

N S

α

α

ϕ

Хай площина задана рівняннямN rr + D = 0 , а пряма - rr = r0 + Srt . З геометричних міркувань (див. мал.) видно, що шуканий кут α = 900 -ϕ, де α - кут між векторами Nr і Sr. Цей кут може бути знайдений по формулі:

cosα = NNrSSr

sinϕ = ±cosα = ± NNrSSr

Умови паралельності і перпендикулярності прямій і площині в просторі.

Для того, щоб пряма і площина були паралельні, необхідно і достатньо, щоб вектор нормалі до площини і направляючий вектор прямої були перпендикулярні. Для цього необхідно, щоб їх скалярний твір був рівний нулю.

Для того, щоб пряма і площина були перпендикулярні, необхідно і достатньо, щоб вектор нормалі до площини і направляючий вектор прямої були коллинеарны. Ця умова виконується, якщо векторний твір цих векторів був рівний нулю.

53

Поверхні другого порядку.

Визначення. Поверхні другого порядку – це поверхні, рівняння яких в прямокутній системі координат є рівняннями другого порядку.

Циліндрові поверхні.

Визначення. Циліндровими поверхнями називаються поверхні, утворені лініями, паралельними какойабо фіксованою прямою.

Розглянемо поверхні, в рівнянні яких відсутня складова z, тобто ті, що направляють паралельні осі Оz. Тип лінії на площині Хoy (ця лінія називається направляючій поверхні) визначає характер циліндрової поверхні. Розглянемо деякі окремі випадки залежно від рівняння тих, що направляють:

2) x2 = 2py – параболічний циліндр.

54

“Курс вищої математики. Частина 1.”

Поверхні обертання.

Визначення. Поверхня, що описується деякою лінією, що обертається навколо нерухомої прямої d, називається поверхнею обертання з віссю обертання d.

Якщо рівняння поверхні в прямокутній системі координат має вигляд: F(x2 + y2, z)= 0, то ця поверхня – поверхня обертання з віссю обертання Оz. Аналогічно: F(x2 + z2, у)= 0 – поверхня обертання з віссю обертання Оу F(z2 + y2, x)= 0 – поверхня обертання з віссю обертання Ох.

Запишемо рівняння поверхонь обертання для деяких окремих випадків:

Аналогічно можуть бути записані рівняння для розглянутих вище поверхонь обертання, якщо віссю обертання є осі Ох або Оу.

Проте, перераховані вище поверхні є всього лише окремими випадками поверхонь другого порядку загального вигляду, деякі типи яких розглянуті нижче:

55

“Курс вищої математики. Частина 1.”

Сфера: (x − a)2 + ( y −b)2 + (z −c)2 = r 2

Тривісний еліпсоїд:

У перетині еліпсоїда площинами, паралельними координатним площинам, виходять еліпси з різними осями.

56

“Курс вищої математики. Частина 1.”

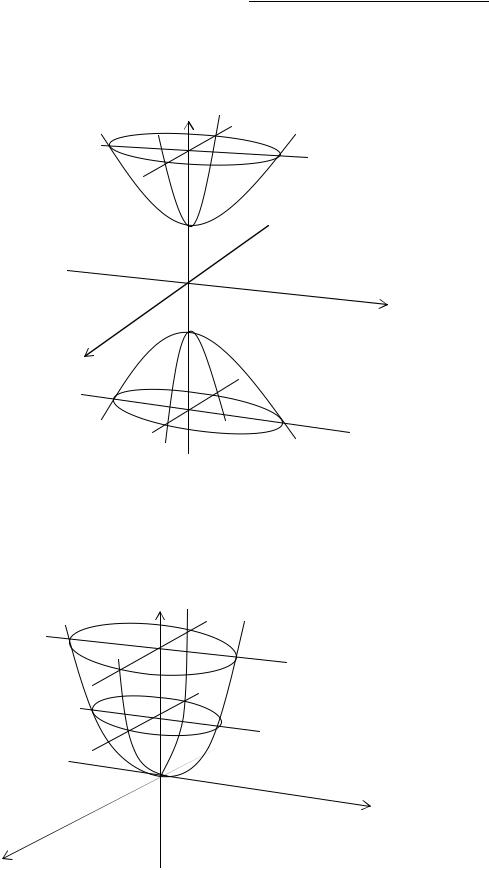
Двуполостний гіперболоїд:

Гіперболічний параболоїд:

57

“Курс вищої математики. Частина 1.”

58

“Курс вищої математики. Частина 1.”

Циліндрова і сферична системи координат.

Як і на площині, в просторі положення будь-якої крапки може бути визначене трьома координатами в різних системах координат, відмінних від декартової прямокутної системи. Циліндрова і сферична системи координат є узагальненням для простору полярної системи координат, яка була детально розглянута вище.

Введемо в просторі крапку Про і промінь l, що виходить з крапки Про, а також вектор nr l, nr =1. Через крапку Про можна провести єдину площину,

перпендикулярну вектору нормалі n .

Для введення відповідності між циліндровою, сферичною і декартовою прямокутною системами координат крапку Про совмещяют з початком декартової прямокутної системи координат, промінь l – з позитивним напрямом осі х, вектор нормалі – з віссю z.

Циліндрова і сферична системи координат використовуються в тих випадках, коли рівняння кривої або поверхні в декартовій прямокутній системі координат виглядають достатньо складно, і операції з таким рівнянням представляються трудомісткими.

Представлення рівнянь в циліндровій і сферичній системі дозволяє значно спростити обчислення, що буде показане дальше.

z

М

ρ

ϕh

r M1

у

OM = ρ; Ом1 = r; MM1 = h;

Якщо з точки М опустити перпендикуляр Мм1 на площину, то точка М1 матиме на площині полярні координати (r θ).

Визначення. Циліндровими координатами точки М називаються числа (r,, h),

які визначають положення точки М в просторі.

Визначення. Сферичними координатами точки М називаються числа (rθ), де ϕ - кут між ρ і нормаллю.

59

“Курс вищої математики. Частина 1.”

Зв'язок циліндрової і декартової прямокутної системами координат.

Аналогічно полярній системі координат на площині можна записати співвідношення, що зв'язують між собою різні системи координат в просторі. Для циліндрової і декартової прямокутної систем ці співвідношення мають вигляд:

Зв'язок сферичної системи координат з декартовою прямокутною.

У разі сферичної системи координат співвідношення мають вигляд:

Лінійний (векторне) простір.

Як відомо, лінійні операції (складання, віднімання, множення на число) визначені по-своєму для кожної множини (числа, многочлени, направлені відрізки, матриці). Самі операції різні, але їх властивості однакові.

Ця спільність властивостей дозволяє узагальнити поняття лінійних операцій для будь-яких множин незалежно від того, що це за множини (числа, матриці і так далі).

Для того, щоб дати визначення лінійного (векторного) простору розглянемо деяку безліч L дійсних елементів, для яких визначені операції складання і множення на число.

Ці операції володіють властивостями:

1)Комутативність x + y = y + x

2)Асоціативність (+) + x y z = x + (+) y z

3)Существует такий нульовий векторO , що O + x = x для x L 4) Для x L існує вектор y = - x , такий, що x + y = O

5)1 x = x

6)α(β x ) = (αβ) x

7)Розподільний закон (α + β) x = α x + x β

8)α( x + y ) = α x + α y

Визначення: Безліч L називається лінійним (векторним) простором, а його елементи називаються векторами.

Важливо не плутати поняття вектора, приведене вище з поняттям вектора як направленого відрізання на площині або в просторі. Направлені відрізки є всього лише окремим випадком елементів лінійного (векторного) простору. Лінійний (векторне)

60