
Vakarchuk_I_O_Kvantova_mehanika_Pidruchnik_B
.pdf
кiлькито радiальнийтут нас розподiлцiкавить непитанняобговорю¹монапрямленостi. хiмiчних зв'язкiв,
|
|
|
ис. 72. Молекула метану. |
|
||||||
|
|
|
суперпозицi¨ |
|
|
|
||||
ãó|si-орбiталiзаксимумтриíîâiìèóíêöi¨,в площинiякi |
|
|
äослiджувализують3гiбридизу¹тьсŸ3енер.Читачеiюпiдяв- |
|||||||
|
Iíøi ëiíiéíi êîìáiíàöi¨ |s |
|
- òà |
|p |
|
|
||||
молекулiипадкуiорисновивченняетиленубудепринципуповеCчас 2Hнутись4. Цю молекулудонього-станiвв.миПриклаВетиленiвжмiнiм |
||||||||||
|siстинилише двi |p |
|
|
|
|
|
|
|
|
||
âç |
|
|
îðáiòàëi, |
|
а- нета три,-орбяк цеутворюютьалiбуло.Ут оримопопередньомуниха |
|||||
. Н хай це будуть- |
|px |
|
|py i |
|
|
|
||||
|
|
|
|
|
|
|
описують розподiл електронно¨ |
|||
кутиУтворимо120 |
|
|
|
|
|
xOy i |
|
мiж собою |
||
|
|
зображзгiдеíî знарисунк.73ом:. |
|
|
||||||
|
◦, якстани |
|
|
|
|
óíêöié |
||||
|
|1i |
= A C1|si + |pxi , |
||||||||
|
|
|
|
|||||||
|
|2i |
= |
B C2|si − |pxi cos 60◦ + |py i cos 30◦ , |
|||||||
|
|3i |
= |
C C3|si − |pxi cos 60◦ − |py |
cos 30◦ . |
||||||
З урахуванням умов нормування цих |
|
|
|
|||||||
702 |
h1|1i = 1, |
|
h2|2i = 1, |
|
h3|3i = 1 |
|||||
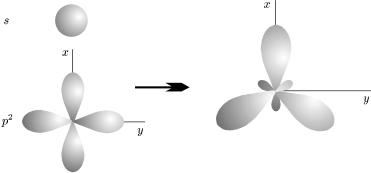
отрима¹мо вирази для2-сталихгiбридизацiянормуванняв молекулi етилену.ис. 73. sp
A, B, C через C1, C2,
C3: |
|
|
C12 |
+ 1 |
| i |
| i |
|
|
|
|
|
|
||||||
| i |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
= |
p |
|
|
|
|
|
C1 s |
+ px |
, |
23 |pyi! , |
|
||||||
|
|
|
|
|
|
|
||||||||||||
|2i = |
|
C |
2 |
+ 1 |
|
C2|si − 2 |pxi + |
|
|||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
ортогональнîñòi: |
|
|
|||||||
|
|
p |
|
2 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
||
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
3 |
|
|
|
||
|
|
|
|
|
|
|
|
âiäïîвiднi рiвняння |
|
C1, |
||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
p |
|
3 |
|
|
|
|
||||||||||
|3i |
= |
C |
+ 1 |
|
C3|s − 2 |pxi − |
2 |pyi! . |
|
|||||||||||
|
2 |
|
|
|||||||||||||||
Не тра аючи загальностi розгляду, уâàæà¹ìî |
|
|
||||||||||||||||
ìè âНакладемоели |
|
|
|
|
|
умови |
|
|
|
|
|
C1, C2 |
, C3 |
|
||||
÷инамина. цi |
|
àíè |
|
|
|
|
|
|
|
|
|
|
|
|
äiéñíè- |
|||
Iз цих умов легкоh1|2i одержу¹мо= 0, h1|3 |
= 0, |
|
|
h2|3 =äëÿ0. |
величин |
|||||||||||||
C2, C3: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C1C2 − |
1 |
= 0, |
|
|
|
|
|
703 |
|||||
|
|
|
|
|
2 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C1C3 − |
|
|
= 0, |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
√ |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
3 |
|
|
|
|
|
|
|
|
||||||||
Iз перших двох рiвнянь цi¹¨ системи |
|
знаходимо, що |
|
|
||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||
|
|
|
C2C3 |
+ |
|
2 |
− |
2 |
! |
|
= 0. |
|
|
|
||||||||||||||||||
ñòàí iõ äâîõ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C2 = C3, ç |
||||
¹ìî çíак + . Остаточно,.при¹днуючиОтже, |
ñòàí |
|
|
√ |
|
. Ôiêñó- |
||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||
|
|
|
C1 |
= C2 |
|
|
|
|
|
|
|
C1 = C2 |
= C3 = ±1/ 2 |
|||||||||||||||||||
ðáiòàëi sp2-гiбридизацi¨: |
|
√2 |si + |pxi , |
|
|
|4i = |pz i, отриму¹мо |
|||||||||||||||||||||||||||
|
|1i = |
|
r 3 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
! , |
|
|
|||||||||||||||
|
|2 = |
|
r |
|
|
|
√ |
|
|s − |
|
|pxi + |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|py |
|
|
||||||||||||||||||||
|
|
3 |
|
|
2 |
2 |
|
|
||||||||||||||||||||||||
|
|
|
|
2 |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
площиíi, |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
орбiталейПритвореннi молекули. C2H4 атоми водню пiд'¹днуютьс äî |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
√3 |
|
|
|
||||||
льно пе екриваютьс|2i, |çâ'ÿçîê3 |
|
|
|
вуглецю. Орбiталi |1i атомiв вуглецю си |
||||||||||||||||||||||||||||
|
|
|
àòîìiâ |
|
|
|
1 |
|
|
|
|
|
σ-зв'язок. Перекриттструктурнаанiв |
|||||||||||||||||||
|
|
|
|
|
r |
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
√3 |
! , |
|
|
||||||||
|
|3 = |
|
3 |
|
|
√2 |s − |
2 |px |
− 2 |py |
|
|
||||||||||||||||||||||
|ò4огоурПрикладомπ |
iþ |
|
|
|
ìiæ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ìiíiìiçó |
|
|
|
|pz . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
напрПершiямкутриорбiталi|4 = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
що ¹ перпен икулярною |
|||||||||||||||||
|
|
|
|
|
лежатьутворюють |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
||
ó.твовищеð¹ю¹енервмолекупотрцi¹¨лiйногомолекули,Nатомамизв'язкущоймiж.поясню¹Самеатомами,акий¨¨простонабiркрiмовуорбiталейозгляну |
||||||||||||||||||||||||||||||||
îðìó |
òàêà: |
|
|
|
|
|
2, ¹ молекула ацетилену C2H2, |
|||||||||||||||||||||||||
У цьому випадку ма¹моH − C ≡ C − H. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
нiйна комбiнацiя з хвильовихsp-гiбридизацiю,ункцiй |
|
коли утворю¹ться лi- |
||||||||||||||||||||||||||||||
704 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|si- та дного з |pi-ñòàíiâ. |
||||||||
Нехайорбiталi:це буде |pxi-стан. Легко знаходимо чотири ортонормованi
|
|
|
|1i = |
√2 |s + |pxi , |
|
|
|||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
датному напрямку осi xçâ'ÿçîê,ñòàí|2 дiлу вiд'¹мному. При утвореннi |
|||||||||||||||||
|1 |
ма¹ максимум розïî |
|
|
електронно¨ густини |
äî |
||||||||||||
|
|
|
|2i |
= |
√2 |
|s |
− |px |
|
|
|
|
|
|||||
|
|
|
|
|
|
1 |
|
òîìiâ |
|
|
ëåöþ, |
|
|
||||
|
|
|
|2 . Стани |1 |
|
|
|
|
|
|||||||||
молекутабливуглецюповчальноТакiпопереднiхдвiйнихлахцiкiз.цимиповернутисьзв'ямолекули,жзавершимокiвстанамàâi нихснуютьякдоприкладбензол,¹цихакимибутхтомаж,доàäi¹íякнихвуглецю.у.Теперщойноiíøi,одного.чмирозгтачевiрозгдинарнлянутатомiвлядабулоèõ- |
|||||||||||||||||
|
|
|
|3i |
= |
|py i, |
|
|
|
|
|
|
|
|
|
|||
|
|
ðîçäiëàõ |
iншого |
|
|
|
|
|
|
|
|
|
|||||
Ñòàí |
|
|
прикладiв |
|
|
|
|
||||||||||
|
|
|4i |
= |
|pz i. |
|
|
|
|
|
|
|
|
|
||||
молекуличерезCлецю |
2станиH2 атоми водню вступаютьвуг зв'язок з атомами вуг- |
||||||||||||||||
На цьому ми |
|
|
|
аналiз властивостей хi |
iчного |
|
|||||||||||
. Зазначимо ли е, що |
|
é iíøi òèïè ìiæàòîìíèõ çâ'ÿçêiâ. |
|||||||||||||||
утворюють силь ий σ- |
|
|
|
перпендикулярнiперекриваючись,донього два |
|||||||||||||
зв'яз к мiж атомами реалiзу¹ться, |
оли розподiл елект |
||||||||||||||||
нно¨ густини в систем |
|
|
|
|
перех довi електрона вiд |
||||||||||||
Йоннийго атома |
до iншого. |
|
Âiíâiäïîâiäà¹òüñ |
внаслiдок |
кулонiвськ |
||||||||||||
π-çâ'ÿçêè óò îðåíi перекр ттям |
|
|
àíiâ |3 |
|
Характери|4 |
|
|||||||||||
лекула кухонно¨ солi NaCl. Узагалi |
ажучПрикладом, зку ежу мiж ого |
||||||||||||||||
¹ деякий ступiньрiзнойменнимийонностi в'язку |
|
|
|
|
ìiæ íøèì, вимiрюють |
||||||||||||
притягання мiж |
|
|
|
|
|
йонами. |
|
|
|
|
цього ¹ мо |
||||||
валентним |
|
йонним зв'я |
утворюом становити неможливо. Завжди |
||||||||||||||
|
|
методом, що |
рунту¹тьсякий,на |
ÿâèùi ядерного |
êâàä- |
||||||||||||
спектральнимТутупольноголонiвськрезонансу |
(äèâ. Ÿ38). |
мiж йонами на деяких характер- |
|||||||||||||||
У металах зв'язок мiж йо ами, якi зануренi в електронну |
|||||||||||||||||
них вiдстанях(електроннийомпенсувiдштовхування¹тьс силами притягання, якi виникають |
|||||||||||||||||
iäèíó |
|
|
ãàç), |
прикладом металiчного типу зв'язку. |
|||||||||||||
45 I. О. Вакарчук |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
705 |
|
унаслiдоколектив |
¨х екрану ання |
|
|
|
. Öå |
|
|
|
¹ |
||||||
багаточа |
è, |
инковим ектомрiдиноюзалежить вiд густини |
|||||||||||||
електрон |
о¨ пiдсисте |
|
електронноюаракт рнi вiдстанi |
¹ |
|
|
|
рiвноваж- |
|||||||
ними мiжйонними |
âiäñò |
|
íÿìè, ÿêi |
реалiзуються в |
екрануваннякрист iчних, |
||||||||||
 |
|
ò ðiäêèõ |
еталах. |
|
|
|
|
|
|
|
|
||||
|
альсi ський тип зв'язку мiж атомамитимирозглянемо |
||||||||||||||
докладнондервнаступному |
|
|
. |
|
|
ð ÷ âè è, äå âií |
|||||||||
Ùå äèí òèï çâ'ÿçêó |
водневий. |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
õiìiøî¨èéìà- |
|
|
|
|
|
|
|
|
|
|
|
|
|
ченнякисоголено¨ювií |
||
|
|
|
|
|
|
|
|
|
|
|
овоктро |
|
|||
|
|
|
|
|
|
|
|
|
|
|
å |
|
|
|
|
|
|
|
|
â.Укисню'язокатисьСиливпараграмолекулiживихма¹доВантакиматомиелектронеособливоорганiзмахiHдерOПрикладомчичастинаВаальсавелат.частквногоеелзна |
|
|
|||||||||
|
|
процесах. жзмiщенаВодневийпритягу¹дваводаобмiнуŸ 90донейтральнi.з |
|
|
|
|
|
|
|
|
|||||
|
|
íèõ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
згляньмоi |
|
|
|
|
|
|
|
|
|
|
|
|
||
àìîðеалiзу¹ться,водню |
|
|
|
|
|
2 |
|
|
|
|
|
|
|||
ïðîò |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
бiлкмолекули |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
i |
B |
зарядами ядер |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
òîíiàíiâ |
||||
iзоль. ованихамiльтонiанатмтако¨ системи |
|
|
|
|
|
|
|
|
|
|
ZA |
|||||||||||||||||
клада¹ться iç ñóìè ãàìiëü |
|
|
||||||||||||||||||||||||||
ZB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ядра т електронiâ атомаˆ |
|
ˆ |
ò |
енер i¨ кулонiвсько¨ вза¹модi¨ |
U |
|||||||||||||||||||||||
|
|
|
|
|
|
HA |
|
|
|
|
HB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
A ç óñiма частинками атома B: |
|
|
||||||||||||||
ˆ |
|
|
|
ZAZB e2 |
|
|
|
|
|
ZA |
ZB |
|
|
|
|
e2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
U |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
RA |
− |
RB |
| |
|
=1 j=1 |
|
RA + rAi |
− |
RB |
− |
rBj |
| |
|
|
||||||||||||
|
|
| |
|
|
|
|
|
|
X X |
| |
|
|
|
|
|
|
||||||||||||
|
|
|
ZA |
|
|
ZB e2 |
|
|
|
|
|
ZB |
|
|
ZAe2 |
|
|
|
|
|||||||||
Òóò |
− |
|
|
|
|
|
|
|
|
|
|
− j=1 |
|
|
|
. |
|
|||||||||||
|
|
=1 |
|
RA + rAi |
− |
RB |
| |
|
RA |
− |
RB |
− |
rBj |
| |
|
|||||||||||||
|
|
X | |
|
|
|
|
|
|
|
|
|
|
|
X |
| |
|
|
|
|
|||||||||
RA, RB |
оординати ядер атомiвелектронаA B; rAi, rBj |
|
|
|
||||||||||||||||||||||||
ñâ ¨õ ÿäåð:-ãî åëåêтрона атома Aiþj-ãî |
|
|
|
атома B |
|
|
|
|||||||||||||||||||||
нумеру¹мо |
rAi |
=ñîìri − RA |
rBj |
= rj − RB . Електронивiдштовхуванняатомi A |
||||||||||||||||||||||||
îïå |
iíäåê |
i, |
|
|
|
|
àòîìi B декядромj. Ïåð |
èé äî îê |
||||||||||||||||||||
ìiæëêò |
. |
ˆатомаДругийзображдоданок |
|
|
|
|
|
|
|
ñüê |
ãî |
|
|
|
данокìiæíÿ |
|||||||||||||
|
|
U |
|
|
|
๠електронамиенерцекулонiверiя |
|
|
|
|
|
|
|
|||||||||||||||
åядромнектоядрамиi¹юàòîðiпр тяганняA à |
|
|
|
|
|
|
атомаатома B. Третiй довiдноснорадiу¹- |
|||||||||||||||||||||
останнiй до анок електронiвце енер iяопе итяганняA |
електронiватомаB.атомаНареш |
|||||||||||||||||||||||||||
атома |
|
|
|
|
|
|
чином, |
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|||||||
òîìíî¨ âçà¹ì äi¨.. Таким |
|
|
|
îð |
ˆ опису¹ енер iю мiж - |
|||||||||||||||||||||||
706 |
|
A |
|
|
|
|
|
|
|
|
U |
|
|
|
|
|
|
|
||||||||||

|
Ìè ïîñò |
|
собi за мету розр хувати енер iю вза¹модi¨ мiж |
|||||||||||||||
атомами залежнавимо |
вiд вiдстанi мiж ними. Будемо розглядати опе- |
|||||||||||||||||
операторˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U як збурення, уважаючи гамiльтонiаном нульово¨ задачi |
|||||||||||||||||
|
|
ˆ |
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
HA + HB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
добуток хвильовиха хвильовоюункцiй атомiвункцi¹ю нульового наближення |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
êè |
зробимоенер iйдеякiатомiвпростiметодомперетвореннястандартно¨Aоператорiеорi¨B. Знайдемозбурень. ористовуСпочпопр |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
доючиданкуоператорв змiщення, запишемо âираз пiд сумамиU . Викв другомó- |
||||||||||||||||||
|
|
ˆ |
àê: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
e− |
r |
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
e |
|
|
âçà¹= |
операторадi¨ |
|
|
, |
|
|
|
|||||
де радiус-вектор мiжатомно¨Ai Bj |
R |
|
|
|R + rAi − rBj | |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
ì |
R = RA −RB |
в операторi |
||||||||
радi¹нта похiднi беруться за к |
|
понентами вектора, а |
|
|||||||||||||||
випису¹мо й наступнi доданки |
|
|
|
|
|
|
|
|
|
|
R. Ïîäiáíî |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U . У результатi |
||||||
|
|
|
|
ZA |
ZB |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
X X |
|
|
|
|
|
|
|
e2 |
|
|||||
Якщо ввести Uоператориˆ = |
r |
|
|
|
|
e−rBj |
|
|
|
|
||||||||
зарядiв(e Ai − 1) |
|
− 1 |
|
R |
. |
|
||||||||||||
|
|
|
|
i=1 j=1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
ZA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆмiжатомно¨ вза¹модi¨Ai |
|
|
|
|
|
||||||||
тодiвиглядувираз для енер i¨QA = e |
|
|
r |
|
− 1) , набува¹ компактного |
|||||||||||||
(e |
|
|||||||||||||||||
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
Формальнийраторизклад експонентиˆ êâàäˆ ˆ+ÿäóïольнихвиразах для |
|
|||||||||||||||||
|
|
|
|
|
|
U = QAQB R . |
|
|
|
|
|
|
||||||
льнихроджу¹ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ ˆ |
|
|
|
дипольних, |
|
|
|
|
|
|
i вищихQA, QB |
|||||||||
|
|
ìåíòiâ:ï |
|
ð |
|
|
|
|
|
|
мультиïî- |
|||||||
|
|
|
|
|
|
ˆмоменту |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
A |
) + · · · , |
|
|
|
|
|
|
||||
де оператор дипольногоQA = (d |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
ZA |
|
|
|
|
|
|
|
|
|
45* |
|
|
|
|
dA = e |
X |
rAi. |
|
|
|
|
|
707 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
i=1

|
|
|
|
|
тепер ряд теорi¨ збурень для повно¨ енер i¨ атомiв, |
|||||||||||||||||||||||||||
що Випишемознах дяться |
|
основному станi: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
(0) |
|
|
(1) |
|
|
|
(2) |
|
·iç· ·ñóìè. |
енер iй основ- |
||||||||||||
нихЕнерстанiвiя нульатомiвового Eнаближ= E åííÿ+ Eсклада¹ться+ E + |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
EA ò |
|
|
içîëü |
|
|
|
|
|
àòîìiâ |
Унаслiдок |
|
||||||||||||||
|
|
|
|
|
|
|
EB : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Перша поправк |
|
|
|
E(0) = EA |
+ EB . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
ВипишемоE äëÿ= íå¨0. Томузагальнийнеобõiäíîвираз: |
|
|
|
|
|
|
|
|
другу попр вку. |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
E |
(1) |
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= h0|U |0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
системинадипольногохвовiй ункцi¨ ,нульовогоде, |
наближення с- |
||||||||||||||||||||||||||
ункцвногзрахîву¹тьсстанучення |
|
|
|
|
|
|
|
|0Ai|0B i |
|
|
|0A |
|
|0B |
|
ùîâi |
|||||||||||||||||
дорiвсереднюютьi¨ знаосновногонулевi ану|0 = |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ованихмоментурозрахуватитома. основномутого,хвильстан |
|||||||||||||||||||
|
|
n = (nA, nB ), m = (mA, mB ) |
|
|
|
|
|
|
|
числа, |
|
|
|
|
|
|||||||||||||||||
правка |
(1) |
|
|
|
h0A|dA|0A |
|
= 0, h0B |dB |0B i |
= 0, то перша по- |
||||||||||||||||||||||||
|
|
|
|
|
|
|
E(2) |
= |
X |
|
|
|Umn|2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
n |
|
|
m(n6=m) En(0) − Em(0) |
|
|
|
|
|
|
|
|
|
||||||||||||
тутстани системи двох атомiв, де |
|
|
квантовi |
|
|
|
|
|
|
що нумерують |
||||||||||||||||||||||
для iзольов них атомiв, |
|
|
|
|
nA, mA |
nB , mB квантовi числа |
||||||||||||||||||||||||||
|
|
|
матричнийвк для енерелементi¨ основного стану, якщо |
|
|
ÿâíié îðìiˆ . |
||||||||||||||||||||||||||
розписатиДруг попр |
|
|
|
|
|
Umn матричний елемент оператора U |
||||||||||||||||||||||||||
ма¹ такий вигляд: |
|
ˆ |
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
ˆ+ |
|
|
1 |
, |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
708 |
|
|
Um0 |
= hm|U |0i = hmA|QA|0AihmB |QB |0B iR |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
X |
|
|
|
|
|
ˆ |
|
|
|
ih | |
ˆ+ |
|
|
i |
1 |
2 |
|
|
|
|||||||
|
|
|
E |
|
|
= |
|
|
|
|
|
− |
|
|
|
|
|
− |
|
|
|
| . виразу для |
||||||||||
|
|
|
|
(2) |
|
|
|
|
|
mA |
|
QA 0A |
|
mB |
QB |
0B |
|
R |
|
|
|
|
|
|||||||||
|
Оскiльки рiзниця |
|
|
|
EA |
|
входить у знаменник |
|
|
|
||||||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
EA |
|
+ EB |
|
|
|
EB |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
mA,mB |
|
|
|
0 |
|
|
|
|
mA |
0 |
|
|
|
|
mB |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
E(2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(0) |
|
(0) |
|
|
A |
|
|
A |
|
|
B |
|
|
|
|
B |
|
|
|
|
|
|
|
|
||||
|
|
, ì๠âiä'¹ìíèé çíàê: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
E0 |
|
− Em = E0 − EmA + E0 − EmB < 0, |
|
|
|||||||||||||||||||||||||

то друга поправк |
|
åíåð i¨ |
сновного стану ¹ вiд'¹мною вели- |
|||||||||||||||
чиною. Це означа¹, |
ùî |
вза¹модiя мiж атомами, яка опису¹ться |
||||||||||||||||
поправкою |
E |
(2) |
випадок, |
|
тер притягання. |
|
|
|
|
|
||||||||
|
|
, ì๠õàðàêоли беремо до уваги лише дипольний |
||||||||||||||||
моментозгляньмовоператорах0 |
ïiñëÿ |
|
|
|
|
|
|
|
|
|
|
|
||||||
зарядiв: |
|
|
|
|
|
|
|
|
|
|
||||||||
цьомуˆ наближеннi |
A |
|
|
простих обчисленьˆ |
отрима¹мо |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
+ |
|0B i = |
|
|
B |
|0B i . |
|||
hÓmA|QA|0Ai = hmA|d |
|0A , |
hmB |QB |
−hmB |d |
|||||||||||||||
|
|
|
|
|
|
|
E(2) = − |
const |
, |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
R6 |
|
÷èìî, |
|
|
|||||||
|
|
вандерваальсiвськ |
|
|
|
|
|
|
|
|||||||||
|
|
|
m ,m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ченням, |
|
|
|
|
|
|
|
|
|
|
|
|
|
Ваальса, |
||||
|
|
|
|
|
|
|
|
|
|
потенцiально¨ |
2 |
|||||||
|
|
|
A |
B |
|
|
|
|
|
− |
|
|
− |
|
|
|
|
|
const = |
X |
|
|
3 |
dmA A,0n |
dmB B ,0n − dmA A ,0dmB B 0 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
EA |
|
EA + EB |
|
EB |
|
|
|||
|
|
|
|
|
|
|
|
|
mA |
|
0 |
mB |
0 |
|
|
|
||
dAmA 0 = hmA|dA|0A , dBmB ,0 = hmB |dB |0B
обмi i¹юимй векторвза¹моираздорiвдлядiям,юютьенерсилирадi¹нi¨,о¨причопритмiжвзàяганняовi¹мотомногоувiд¨. ЯкВанпритяганнябадер наназивапротищо, |
||||||||||||||||||||||||
ютьдегуознаЗнайдединичнийенервза¹мо |
|
|
n = R/R |
|
|
|
|
|
const > 0. |
|
|
|||||||||||||
ê |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E(2), взятому зi зна |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
либиноюнадню,ванiкривихстйкихнапростiйкихвiддалях,молекулахякий. Вонимолейшлосяêприводять.¹Зокрема.знаЦiуервiдчпоi¨о |
|||||||||||
|
|
|
|
|
|
них, якiвiдстанiрозташнеямаченьутворюютьг |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
êè |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
тенцiальнапоатомнiяризованого |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
ìiæ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
âiä'¹ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нiжпато |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
||
ступiдлябтенцiальнiвiдстльшими,виникнеатомарногододi¨Ÿ87,мiжями |
|
степе евим законом 1/R |
|
|
||||||||||||||||||||
− , спадають |
|
|
|
|
|
|||||||||||||||||||
àíi ìiæ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5◦K розташована н |
|||||||||
Знайдемо оцiнку зверху4 A. i знизу ве ичини |
|
|
|
|
|
|||||||||||||||||||
мiжнимиляi¨дво |
ат мами водню. Для |
цьогопiдсумовуваннязнаменникconst для вза¹мовиразi |
||||||||||||||||||||||
øèìconst |
çà |
iним згортй найменш м значенням |
|
|
2 |
íàéáiëü |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3e /4aB |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e /aB |
|
|
|
|
а¹тьсчи ельняо середньогокпiсля |
за основним станомпро |
|||||||||||||||||
квадратст |
нами.велПричиницьому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
òè âiñü |
|
|
|
|
|
|
|
dAn dB n |
|
dAdB )]. Якщо спрямува- |
||||||||||||||
|
|
|
|
|
|
|
|
|
[3( |
|
)( |
|
|
) − ( |
|
|
4 |
h |
(2z zB |
xAxB |
− |
|||
|
|
z уздовж n, то це середн¹ дорiвню¹ e |
||||||||||||||||||||||
2 |
i |
|
4 |
2 |
|
2 |
|
i |
2 h |
2 |
ih |
2 |
i |
h |
2 |
ih |
2 |
i5 |
A2 4 − |
|
||||
2 |
|
|
h 2 ih |
zB |
|
xB |
|
2 |
|
|
|
2 5 |
||||||||||||
yAyB ) |
|
= e (4 zA |
|
+ xA |
|
|
+ yA |
|
yB |
) = 6e aB, îñêiëüêè |
||||||||||||||
hxAi = . . . = hzB i |
|
= aB. Îòæå, ìà¹ìî 6e aB < const < 8e 709aB. |
||||||||||||||||||||||
Точний розрахун. к да¹: const 6.5e2a5B. Äëÿ äâîõ àò ìiâ ãåëiþ
const 1.6e2a5
михзаВажливимЗазначимо,.снаДлязскрапленняякихвза¹мовипаперебурiвноважноготиунаслiдок Bвипадккуiящо. огохвильВонаазусамеа¹омстанузатомiв,виника¹нейтральнихсилимiжсновномузатовiд'¹мнимВанно¨системi,дерзоваякихвза¹моатомiвчастинаВазнченнямльсаднаковихвдi¨основномуутворення¹¹збудженомуаквiдпповнатомiв,званавiдальнистанi¨стiйкогоенеррезочасстi¨-.
iнший добуткiвзбу |
|
|
|
|
|
|
ψ0 |
||
|
|
дженому |
|
|
|
|
|
|
|
áiíàöi¹þ |
виродження, |
|
нульовомухвункцiй:ль |
наближеннiункцiя системилiнiйноюψ(1êîì, 2)-, |
|||||
|
|
|
|
îâèõ¹ψn |
|
|
|||
порцiйноюника¹У цьомувжевипадкудопершомуψ(1, 2)ïîïð= |
|
1 |
[ψ0 |
(1)ψn(2) ± ψ0(2)ψn(1)]. |
|||||
√2 |
|||||||||
|
|
|
порядкуàâêа до теоенерi¨i¨збурень,нульовогоi отже,наближеннявона ¹ прови |
||||||
|
|
|
- |
||||||
|
|
|
|
|
|
|
|
рiдиналя сил Ван дерсистеми,Ваальсаяка. |
|
складДослiдимо¹тьсяз |
квантовi3 Ÿ 91стани. Бозе6багаточастинково¨,як- |
||||||||
|
|
1/R , |
íå äî 1/R |
|
|
||||
iанз декарт вимиN тотожнихоординатбезспiнових бозе-частинок маси m êîæ
|
|
|
|
|
|
|
|
|
|
- |
àêòî¨íсистемицiально¨ковихвза¹модiйдорiвню¹енерi¨, якусувiзьмемокiнетично¨як сумувенероб'¹мiенерi¨ всiхiй. попарчастиамiльтоíèõîê |
||||||||||
íмiжчаст ¨х тпо |
|
|
|
|
|
r1 |
, . . . , rN |
V |
|
|
|
|
|
|
|
Φ(|r − rj |), (i, j) = 1, . . , N : |
|
||||
|
|
|
N |
pˆ2 |
|
|
|
|
|
|
òóò |
|
ˆ |
|
j |
+ |
|
|
Φ(|r − rj |), |
|
|
|
H = j=1 |
2m |
1≤i<j≤N |
|
|
|||||
|
|
|
X |
|
|
X |
|
|
|
|
моделiкий |
вивчають властивостiоператор ако¨льсубагатобозонно¨- частинки.истемиНаосновiякрiдцi¹¨ |
|||||||||
pˆj |
= |
− ~ j |
|
|
|
iìïó |
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
ень,лiйвизначальними,опiчнихнкуоскiлькивантовачастинокмасштабахтутякщоквантмiкр.Квантовомехдояксжинаiту,¹цiканiчнiяскрхвилiавимнiчнiвопринципи,деоб'¹ктомвиявляБройзак |
|||||||
щоють710номiрностiiзичнихвизна4себеHe. дослiджстмкроскютьповедг |
|
|
|
ðiäèíà, |
|
|
||||
|
|
iäêèé |
|
|
|
|
|
|
||

ляв рiдинiспiвмiрна¹ середнябiльша зааньхарактернiчастинкпросторовiми. масштаби, якими
частинiдêèé. 4iдкийHe ¹ вiдстбозе-рiдиною,мiж оскiльки його атоми бозе-
собоюермiони. Далi.Властивосмовайтиме3Heтемперату¹цихсамее iдин-рiдиною,радикальнотомувiщорiзняютьсйогоатомиямiж
когощов частинокявля¹крiзьпрямимтонкiпри.Ценизькихнаслявище,пiляридкомякбезквантовомехтонiаном,багатотертяðàõiíøèõ4незвичайHeнiчного.званеЦяцiкавихявищепринципуiкальназдатвластивостейадплинносiстьбозетотожноспротiк-рiдинаi,-
потенцiченняШрединòа хвильовiОтж4He,àе,льнувлерамонашимжнаснiзункцi¨енерцимвивчати,ункцi¨завданнiюгамiль. .рядЗÿцi¹юкщоФур'¹:метоюрозв'язатизнайтитобторозклйогознстацiонарнеàенерйтидемойогоетичнийдвочастинковувласнiрiвнянняспектрзна-
|
|
àìiëü |
1 |
X |
|
eik(ri−rj ) |
|
|
ν0 |
|
|
1 |
X |
|
eik(ri−rj ), |
||||||||||||||
|
Φ( r |
|
r ) = |
|
|
V |
|
|
ν |
= |
|
+ |
V |
|
|
ν |
|||||||||||||
|
| i − |
j | |
|
|
|
k |
k |
|
|
|
|
|
|
|
|
|
|
V |
|
k6=0 |
k |
|
|
||||||
де величина |
|
|
|
Φ(R) dR, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
i |
νk = Z e− |
kR |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
запишемо г |
|
тонiан нашо¨ системи так: |
|
|
|
|
|
|
|
|||||||||||||||||||
|
X |
pˆj2 |
|
|
|
|
|
|
X |
|
|
|
|
|
N |
|
X |
|
|
|
|
|
|
Справдi, |
|||||
|
Hˆ = |
|
+ |
|
N (N − 1) |
|
ν |
0 |
+ |
|
|
|
ν |
(ρ ρ |
|
− |
1) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
j=1 |
2m |
|
|
|
|
2V |
|
|
|
|
|
|
2V |
|
|
|
k |
|
k |
−k |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k6=0 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
1 |
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
e− |
kr |
, |
|
k = 0 |
|
|
|
|
|
просторуза |
||||||||
означенням,¹ кое iцi¹нтомгустинаФур'¹ρ =÷àñòè |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
люктуацi¨нок системигустиниj в деякiйчастинокточцi. |
|
||||||||||||||||||
|
|
|
|
k |
|
|
|
√N j=1 |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
X |
δ(r − rj ), |
|
|
|
|
|
|
711 |
|||||||||
|
|
|
|
|
|
|
|
n(r) = |
|
|
|
|
|
|
|
|
|
||||||||||||
j=1
