
Vakarchuk_I_O_Kvantova_mehanika_Pidruchnik_B
.pdf
цеПiдрахуознача¹мо, щоймовiрнiсть перехпричомуду,коли τ |
|
→ ∞, |
|
а актично |
||||||||||||||||||||||||||||||
ми працю мо |
|
|
межах теорi¨, збурень. Тепер дивимось, наоскiлькивираз |
|||||||||||||||||||||||||||||||
|
|
|
ωf τ |
1 |
|
|
|
|
|
|
|
|
|
|Vf i |
/~ωf |
|
| |
|
1 |
|||||||||||||||
|
ωf τ |
|
|
ωf i |
|
2 |
ÿê íà |
дне з представлень |
δ- óíêöi¨ (äèâ. Ÿ5): |
|||||||||||||||||||||||||
sin2 |
2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
2 |
|
|
|
|
|
sin |
2 ωf iτ |
|
|
ωf i |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
квантового числащотакийlimïåðåõiä ìà¹= çìiñòπδ |
ëèøå. |
для неперервного |
||||||||||||||||||||||||||||||||
Çðîçóìiëî, |
|
|
|
|
|
τ →∞ τ |
|
|
ωf i |
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
f . Отже, при великих значеннях τ |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Vf i 2 |
|
|
ωf |
. |
|
|
|
|
|
|
|||||||||
|
|
|
|
iнтервалщоцявеличинаквантовогоïîâ'ÿ÷занаисла з |
2 |
|
|
|
|
|
|
|||||||||||||||||||||||
одиЗазíаичнийимо, |
|
|
|
|
|
Wi→f = |
|
| ~2| |
|
τ πδ |
|
|
|
|
|
|
перехквантовихдуна |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
éìîâiðíiñòþ |
|
||||||||
переходiв |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f , а швидкiсть |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
w |
|
|
|
|
|
= dWi→f |
|
|
|
|
|
|
|
|
|
|
|
|||||
äîðiâíþ¹ |
|
|
|
|
|
|
|
|
|
|
i→f |
|
|
|
|
dτ |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Vf |
2 |
πδ |
ωf i |
. |
|
|
|
|
|
|
||||||
Беручи до уваги |
w →f |
= |
|
| |
| |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
~2 |
2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
властивiсть δ- óíêöi¨, |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
ωf |
|
|
|
|
|
Ef(0) |
− |
E(0) |
|
~ |
|
|
|
(0) |
|
|
|
(0) |
|
|
||||||||||||
остаточно çíаходимо |
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
, |
||||||||||||||||||
|
|
2~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
δ |
|
2 |
|
|
= δ |
|
|
|
|
|
|
|
|
= 2 δ Ef |
|
− |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
|
2 |
|
(0) |
|
|
|
(0) |
|
|
|
|
|
|
|||
ною -числоменучасучено¨р.i¨ якпривцьомуiмовiрнiстьк антовихарактеризу¹тьсяперехзабезпечу¹одуодахза. виконаодиницюнеперервнимнячасу,законуцi¹¨кванвелиоберзбе- |
||||||||||||||||||||||||||||||||||
товимнчирДельженняОскiлькии,таознадо |
|
|
|
w →f = |
~ |
|Vf |
| |
|
δ |
Ef |
|
− Ei |
|
. |
|
|
|
|||||||||||||||||
|
|
|
|
|
êöiÿ |
|
|
|
âèðàçi |
|
|
|
|
|
|
|
|
|
îçìiðíiñòü |
|||||||||||||||
|
|
|
|
|
|
кiнцевий |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
462 |
|
|
|
|
|
|
|
f , òî |
швидкiсть переходу з початкового стану в |
|||||||||||||||||||||||||

будь-який кiнцевиé отриму¹мо iнте руванням за всiма значення-
ìè f :
w = |
2π |
Z |Vf |2 |
(0) |
(0) |
df |
~ |
δ Ef |
− Ei |
|||
|
|
|
|
|
|
Уведемо величину= |
2π |
Z |
|
Vf |
2δ |
|
E(0) |
|
|
E(0) |
df |
dE(0). |
|||
|
|
|
|
|
|
||||||||||
~ |
|
| |
| |
|
|
f |
− |
i |
|
dEf(0) |
f |
||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
(0) |
|
|
|
df |
|
|
|
|
||
íàти:звемонадиничнийгустиною |
ρf |
(Ef |
енерстанiвi¨. |
Теперiяка iнтедорiвню¹руваннякiльклегкостi |
|||||||||||
викостанiвяку |
|
|
) = |
dE(0) |
, |
|
|
|
|||||||
|
|
|
|
êiíöåâèõ |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
f |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
iнтервал |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
2π |
|
|
(0) |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
стиноюдмаОбчислимоугомумякчином,азолоткiнцвадратнаближеннi,åiнтенвихймовiрнiстьправилоивнiстьтричногонiвберучиФепквантквантовихмiпочатк8.доелементавогоуваги,перехперехенероператоращодiвдувi¨н.зашомувизнача¹тьсЦядиницюзбуормувипадкеннялачасувевiт |
|||||||||||||||
поправкдгуличТак |
|
|
w = |
~ |
ρf (Ei |
|
)|Vf |
| . |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
âié |
|
|
|
|
|
Ôåðìi (1901 1954) |
|
àëiéñü |
|
t′ |
|
||||||||||
|
|
|
|
|
|
лабораторi¨ |
t1 |
|
|
|||||||
|
Cf(2) = |
|
2 |
|
|
|
|
|
|
Z |
dt′ eiωf f ′t′ |
Z |
dt′′ eiωf ′it′′ |
|||
|
~ |
|
f ′ |
Vf f ′Vf ′ |
||||||||||||
|
|
повiльними |
|
|
|
|
|
t0 |
|
t0 |
|
|||||
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
||
|
|
|
2 |
|
|
|
|
|
|
t1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Чик. ийазькогоатомно¨радiоактивносiзик,унiверситебомби1942.роцiòËàói,ó,спричинено¨б побуеатавдувавНобечасть463- |
|||
першийствореннi8Енрiкдуваннямядернийпремi¨т1938виреакторробовуврокузàннiвiдкриттянейтронамиамериканськiтштучно¨ |
|
|
||||||||||||||
бомбарлiвсько¨у |
= ~ |
|
|
f ′ |
Vf f ′Vf ′ |
Z |
|
dt′eiωf f ′t′ |
|
|
||||||
|
|
|
|
X |
|
|
|
|
t0 |
|
|
|
|
|
|
|

|
eiωf ′it′ − eiωf ′it0 |
= |
1 |
|
2 |
X |
Vf f ′Vf ′i |
|
× |
|
|
|
|
|
|
|
|
iωf ′i |
|
i~ |
|
f ′ |
iωf ′i |
|||
Теперf ′ доданок з f ′ |
= i не да¹ внеску i тому äàëi éîãî íå âðàõ |
¹ìî. |
||||||||||||||||||||||||||||||||||||||||||
|
|
× |
|
eiωf it1 |
− eiωf it0 |
− |
eiωf ′it0 |
eiωf f ′t1 |
|
− eiωf f ′t0 |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
iωf i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
iωf f ′ |
|
|
! |
|
|
|
|
|||||||||||||||
|
скориста= |
|
i~ |
|
|
òèì,e |
ùî |
|
|
|
|
|
|
|
|
|
|
|
− |
|
− |
|
|
|
|
− |
|
|
|
!, |
||||||||||||||
|
|
|
|
|
|
iωf ′i |
|
|
|
|
|
iωf |
|
|
iωf f ′ |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f ′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
X |
|
Vf f ′Vf ′i |
|
iωf iτ |
|
1 e |
iωf f ′τ |
1 |
|
|||||||||||||||||||
ìè |
|
|
|
ëèñü |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
çà |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωf f ′ + ωf ′i = ωf i. Зауважимо, щоовусумi |
|||||||||||||||||||||||||
|
(1) |
|
|
|
|
|
(2) |
|
|
|
|
eiωf it0 |
" |
eiωf iτ |
− |
1 |
|
|
|
|
|
X′ |
|
Vf f Vf |
i |
! |
||||||||||||||||||
|
Cf |
|
+ Cf |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
Vf i + |
|
|
|
|
|
|
′ |
′ |
|
|||||||||||||||
|
|
|
|
|
|
|
i~ |
|
|
|
iωf |
i |
|
|
|
|
|
|
|
~ωif ′ |
|
|
||||||||||||||||||||||
iндекуâадратнихîâiðíiñòü |
|
|
|
|
|
|
|
ïðè |
|
|
|
|
|
|
|
|
|
|
|
|
τпiдсумовування.Другйдо |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(f ′=i) |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
#. |
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
¹тьсяЧасовийзтимножник+, ùî ìè |
|
|
|
|
~ωf ′i |
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
iωf f ′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
X′ |
Vf f ′Vf ′ |
|
|
eiωf f |
′τ |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
рування), |
|
|
|
скiнченну |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
дужкмалипершомв ушомудоданкуаближеннi,величинуквадратнихi отжйде,дужкахпри збiг |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(f ′= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
âií ä๠|
i |
|
|
|
|
|
|
|
|
|
|
перех ду лiнiй ий внаслiдокза |
|
|
|
|
|
|
τ → ∞ |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
τ |
|
|
−∞ |
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
çà |
|
сом промiжного стану |
→ ∞ |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
âiäë |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
î,9якого,Дляпро iлюстрацi¨iнтеможна зробитисказаногоiда¹детальнiшийрозгляньмо(а аналiзпрактичнопростий( приклад,9мова.Томувiдштовхуючисьйогояк внесокправи |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f ′ |
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (ω) хороша ункцiя): |
|||||||||||||||
|
|
|
|
|
|
|
∞ dω f (ω) |
eiωτ − 1 |
= Z ∞ dx f (x/τ ) |
eix − 1 |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
iω |
|
|
|
|
|
|
|
|
|
|
|
|
ix |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
= |
f (0) |
|
|
∞ dx |
eix − 1 |
|
= f (0) |
|
∞ |
cos x − 1 |
dx |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
τ →∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
ix |
|
|
|
|
|
|
|
|
|
|
|
ix |
|
|
|
|
|||||||||
464 |
|
|
|
|
+ |
|
∞ |
sin x |
dx |
|
|
= f (0) |
∞ |
sin x |
dx = πf (0). |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
−∞ |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
−∞ |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||

|
êðóãквантовихгомунаближеннi,наближеннiпростийперехякщодiврезультат:дорiвню¹приньомуймовiматричнийвиразудо iвню¹нiсть,якийелементквантовогонулевiми знай. Т |
|||||||||||||||
шлиперехкиму швидкiстьймовiчином,педушомдротриму¹мо |
|
|
|
|
|
τ → ∞ |
|
|
|
|
|
|||||
замiнитиаближено |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Vf i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
ðíаi:сть квантовоголудужку вперехпопереднiйдуза |
диницюормулi.часуОтже,в остаточдругому |
||||||||||||||
|
|
|
|
|
|
ïiä |
|
|
|
|
|
öié |
|
|
||
÷èíè |
Ÿ 57. îçñiÿííÿ |
|
äîñëiäæäè), |
у конденсованих тiлах |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
f ′ |
E |
|
|
Ef ′ |
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
− |
|
|
|
|
|
|
|
|
|
|
2π |
|
|
|
|
Vf f ′Vf ′i |
|
(0) |
|
|
(0) |
|
|
||
речовинiважлиУрахуз першимане,(äâîяапридруг10отоннiêë. ад,го придоданкаперех |
|
колиеннiз акомпроцесiввiн¹модногодулярозсiяннявпорядкусвiтлаормулiвелив- |
||||||||||||||
|
wi f = |
|
Vf + |
′6 |
|
|
|
|
|
δ Ef |
− |
E |
|
. |
|
|
|
→ |
~ |
|
|
|
(0) |
|
(0) |
|
|
|
|
|
|
||
äèìî |
|
ðîçñiÿ |
нейтронiвiв у речови . Будемо |
|
àòè, |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Як иклад |
|
|
|
ñò |
|
íî¨ |
|
збурень дослi |
що стан речовини при прох джен ацiонанейтрона теорi¨ |
ÿ. Iíàê |
|||||||
ча¹ сво¹¨проблемуен i¨. Ст |
нейтрона до |
ðîçñiÿííÿ |
характеризу¹ться |
|||||
ше кажучи, розгляда¹мо пружне ðîçñiÿííÿ, коли нейтронвважне ра- |
||||||||
|
|
|
|
вiльнийk′ хвильовою ункцi¹ю |
||||
|
початкова хвильова ункцiязмiню¹тьсплоскою |
|||||||
õâèëею:ьовим векторомзастосуванняk, |
|
ñïåêòðiâ |
|
|
||||
|
åîðiÿ |
|
|
|
|
|||
|
(0) |
|
|
|
1 |
ikr |
але зi змiненим за |
|
Пiслямкомрозсiянняхвильовимма¹монапр ψвекторомзнову= | = |
√ |
нейтрон,e . |
||||||
|
|
|
|
|
V |
|
|
|
нальн3010ДI.èОвй..ВакарчукунiверситетI.О.Вакарчукiменi.ТIвана(0) |
Франка,зоряних 2001 2. k′r. Львiв: Львiвський нацiо465- |
|||||||
|
ψf |
= |f i = |
√ |
e |
|
|
||
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|

ì ¹ ç |
|
iñò ê å iöi¹íòà Ôóð'¹ люктуацi¨ ÷èñëà àòîìiв середовища. |
||||||||||||||||||||||||||||||||||
Òàêèì ÷èíîì, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пiдраху¹мо повну ймовiрнiсть розсiяння у всiх напрямках: |
|
|||||||||||||||||||||||||||||||||||
|
|
тiлесного |
|
2π |
N |
|
|
|
|
|
|
|
|
|
|
|
~2k′2 |
~2k2 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
w →f = |
|
|
V 2 |
|νq |2|ρq|2δ |
|
2m − 2m ! |
|
|
|
|
|
||||||||||||||||||||||
|
|
~ |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
X |
V |
Z |
dk′wi→f |
= |
|
V |
|
|
dΩ Z |
k |
′2 |
dk′ wi→f . |
||||||||||||||||||||||
w = |
k′ wi→f = |
(2π)3 |
(2π)3 Z |
|
||||||||||||||||||||||||||||||||
Ми перейшли до с å èчно¨ системирозсiкþ¹òüñнейтрона:динат,пр |
îìó |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
ðîçñióÿннякомуяк вiдношенняейтронвеличини. |
dΩ |
¹ åëå |
|||||||||||||||||||||||||||||
ментомУведемо перерiзкута, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
чатково¨ густини потоку налiтаючого |
|
|
|
|
|
|
|
|
|
|
|
|
w äî ïî- |
|||||||||||||||||||||||
|
|
|
|
|
σ = w m × V |
, |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~k |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
mV V |
|
|
|
|
|
′2 2π N |
2 |
|
2 |
|
|
|
~2k′2 |
|
|
|
~2k2 |
! dk′. |
|||||||||||||||||
σ = |
|
|
(2π)3 Z dΩZ k |
|
|
|
|
|
|
|
|
|νq | |ρq| × δ |
|
|
|
|
− |
|
||||||||||||||||||
|
~k |
|
|
~ |
|
V 2 |
|
|
2m |
2m |
||||||||||||||||||||||||||
Використà¹ìî властивiсть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
δ- óíêöi¨: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
~2k′2 |
|
|
|
|
~2k2 |
|
|
|
δ(k′ |
− |
k) |
. |
|
|
|
|
|
|
|
||||||||||||
Теперсiянняiнтеостаточнорал легкознаδ õîäèáåðåìî:, i äëÿ äè= |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
еренцiального перерiзу роз- |
|||||||||||||
|
|
|
|
|
2m − 2m ! |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
~2k/m |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
dσ |
= |
mνq |
2 |
|
|
òiëà, |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
N Sq |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
dΩ |
2π~2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
¹ структурним актором конденсованого2 |
|
|
|
|
|
|
причому |
|
|
|
||||||||||||||||||||||||||
òóò |
|
|
|
|
|
|
|
|
|
|
Sq = |ρq| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
θ |
|
|
|
|
|
äå êóò ðîçñiÿííÿq = |k′ − k| = pk′2 − 2kk′ + k2 = 2k sin |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
, |
|
|
|
|
||||||||||||||||||||||||||||||
2 |
|
|
|
|
||||||||||||||||||||||||||||||||
30* |
|
|
|
|
kk . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
467 |
|||||
|
|
|
|
θ = d′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
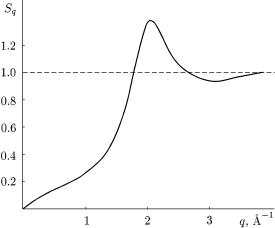
ди Якщоеренцiальнийнейтронперерiзрозсi¹ться на одному атомi, то N = 1, Sq = 1 i
Iнтенс внiсть озсiян dΩ = |
|
2π~2 |
. |
dσ |
|
mνq |
2 |
íÿ íà |
|
|
|
ðåíöiàëüíèì ïåðåðiçîì ðîçñiÿííÿN невза¹монадномудiючихцентрi,центрахзбiльшен¹дèìåâ-
N ðàçiâ: |
Iq = N |
2π~2 |
|
.розсiяння структурномувонденсова- |
||
номуТакимтiлiчином,навза¹мвiднî |
||||||
|
0 |
|
mνq |
|
2 |
|
дiючихшення iнаòомаенсèâíõ äîñòi |
|
|||||
акторовi: |
|
|
|
Iq0 äîðiâíþ¹ |
|
|
руЦе речовдозволя¹отриманий.визначатиНарис.51 |
|
Iqракцiйенийструктуихекспериментнийакторахструрiдêоготу |
||||
|
зобрв диàæ= Sq. |
|
|
|
||
|
|
Iq0 |
|
|
|
|
4кихHe,променiв. у дослiдах |
ðîçñiÿííÿ íåéò îíiâ |
ðåíò åíiâñü- |
||||
468 ис. 51. Структурний актор рiдкого 4He ïðè T = 0◦ K.
Ми говорили весь час про |
|
|
|
нейтронiв, однак резуль |
|||
залиша¹ться |
м самим, якщо |
|
будь-якi частинки: |
||||
|
òèнки,ордаотоничастинкдлярозсiянняпе .ядерiзуозсiюютьсзсiяння.ядра:Мiжiншим,звiдси отриму- |
||||||
¹моатомелектрони,iормулуα-часезер |
|
|
|
|
|||
их ядрах. Справдi, |
|
|
|
α-частинок на |
|||
Кулона, |
|
α- |
|
а вза¹м дi¹ ядром за законом |
|||
νq = 4πe2Z/q2 äå Z çàð |
|
|
|||||
|
|
dσ |
|
me2Z |
|
2 |
|
|
|
|
= |
2 |
, |
||
|
|
dΩ |
p2 |
||||
гамiльтонiанаЦiкавиормулаŸ 58.змiниКвантовiезер¹вiдбува¹тьсзадачi,ордаперехення.колизадиpзбуречастинки=ïiä~q дi¹юня дi¹раптовихраптово,збуреньтобто змiна
раптово¨ |
можна навести |
змiну заряду .атомногоЯкприклад тприк¨ |
τ < 1/ωf |
ядра,ма-розп¹Хвильмаакдi Часу змiнупопрункцiяiвняннiходжзрядусистемиз перiожнадомвважобертатичерезаннямитт¹воюоболонкуелектрона. ÿäðàнавколото- |
|||||||||
β |
им.оващо |
|
|
|
β |
|
|
|
|
|
|
|
|
|
|
|
ψ(0) |
|
|
|
|
|
|
|
(0) |
|
íå ¹ |
привласноюаких раптовихункцi¹ю новогозмiнах гне |
|
мiвстигтонiаа¹правилом,змiни.Оись,же, сталеанвонаψ |
|
||||||||
|
àöiîíàð èé ñòàí |
|
|
|
|
уже не ¹ стацiонарним. Перехiд у |
|||
альнимхвиль |
ву ункцiющозвиплива¹овимг з принципутонiаномсуперпозицi¨розрахову¹мо.власнихозкл |
||||||||
äà¹ìî |
|
ψf |
|
|
|
àìiëü |
- |
||
óíêöié íîâ ãî ãàìiëü |
ψ(0) |
|
у ряд за повною системою |
|
|||||
i |
|
|
|
|
|||||
|
|
|
|
òîíiàíà |
|
|
|
||
Кое iцi¹нти розкладу |
|
ψ(0) = |
Cf iψf . |
|
|||||
|
|
|
|
|
i |
|
f |
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
Cf i = Z |
ψf (q)ψi(0)(q) dq, |
469 |
||||
çãiäíî ç |
|
|
|
суперпозицi¨, i визначають шукану ймовiр- |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
éìîâiðíiñòü |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
нiсть такогопринципомперех ду |Cf i|2 |
= Wi→f : |
|
(q) dq |
. |
|
|
|
|
|
|||||||||||||||||||||||||||
збуреннянiчнийЯк прик |
|
Wi→f = Z |
ψf (q)ψ |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(0) |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
частоту:сновномутого,станi,щолiнiйнийякщораптовегармо- |
||||||||||||||||||||||||||
осциляторзмiню¹адрозраху¹мойогозалишитьсямасуi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m, ω → m′, ω′. Ìà¹ìî |
|
||||||||||||||
де хвильовi ункцi¨ |
|
W0→0′ |
= |h0|0′i|2, |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
hx|0i = |
mω |
|
1/4 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
e−mωx |
/2~, |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
π~ |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
матричнийhx|0′i = |
|
|
π~ |
|
1/4 |
|
e− |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
m′ω′ |
|
|
|
|
|
m′ |
|
|
2 |
|
|
|
~ |
|
|
|
|
|
||||||||||
àõó¹ìî |
|
|
|
елемент: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω′x |
/2 |
|
|
|
|
|
|
|
|||||||||
W0→0′ = |
π~ |
π′~ ′ |
|
|
Z ∞ exp − 2 |
|
|
|
|
~′ ′ + |
~ |
dx |
2 |
|||||||||||||||||||||||
|
|
|
|
m ω |
|
|
|
1/4 |
|
|
|
|
−∞ |
|
|
|
|
x2 |
|
|
|
|
m ω |
mω |
|
|
||||||||||
|
|
mω 1/4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
= |
|
π~ |
π~ |
|
|
r m′ω′ + mω |
. |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
m′ω′ |
|
|
1/4 |
|
|
|
|
|
|
|
|
|
|
2π~ |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
mω 1/4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Остаточно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
Зрозумiло, що при |
W0 0 |
|
= |
|
|
|
|
|
mω |
|
|
|
|
. |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
′ |
rm′ω′ 1 + |
|
mω |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
→ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
m′ω′ |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Аналогiчноелектронулегкmωïîê= азати,m′ω′ iмовiрнiстьщопри W0 |
|
|
|
0′ = 1. |
|
ðíiñòüþ ç |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→ |
|
|
|||||
залишитисьмасовим числом 3 i перетворенняосновномуйого1 β-розпадiйонгелiатома,iмоâîä |
|
|||||||||||||||||||||||||||||||||||
Zрозпаду′)2]3 . 0.702332, äå Z = 1 |
Z′ |
|
|
|
|
|
s- àíi äîðiâíþ¹ [4ZZ′/(Z + |
|||||||||||||||||||||||||||||
|
= 2 заряди ядра до i ïiñëÿ |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 À IX |
|
|
|
|
|
|
|
|
|
ВЗА™МОДIЯ АТОМА З |
ЕЛЕКТ ОМА НIТНИМ ПОЛЕМ |
||||||||||||||||
Ÿ 59. |
|
|
|
вiльного |
|
|
|
|
|
ïîëÿ |
|
||||||
Äëÿ |
|
лiдовного квантовомеханiелектромагнiтногоопису явищ, |
|
ñïî |
|
||||||||||||
стерiгаютьКвантуванняñ при вза¹модi¨ атома ре÷овини з електромагнякiтним |
|||||||||||||||||
що першопоштовõом до орення само¨ |
|
îâî¨ òåîði¨ ñòàâ ïîñ- |
|||||||||||||||
тулат |
Планк |
|
квантування |
åíåð i¨ åëåêòромагнiтноНагада¹мо,поля. |
|||||||||||||
ïî åì, íàì íå á |
|
|
|
|
|
ÿ ïîëÿ. |
|
|
åîði¨ |
||||||||
Важливим ¹ |
ак жiдноте,провестищо резуквантуванатi побудови квантово¨ |
||||||||||||||||
е ектромагнiтногпро |
поля узагальнювались iде¨ й поняття, |
ïîòðiáíi- |
|||||||||||||||
Будемо |
частинокх дити з класич ого опису |
|
|
|
|
||||||||||||
для створення квантово¨ теорi¨ поля як ундаменту iзики еле |
|
||||||||||||||||
ментарних |
|
|
. |
|
квантово¨ |
анiкиелектромагнiтногоздiйс перехiд |
|||||||||||
Äàëi |
|
|
çâè÷ éíîþ |
хемою |
|||||||||||||
представимо його у виглядi |
бору гармонiчних |
|
|
|
|
. |
|||||||||||
вiд клзасичних осциляторiв |
до квантовимех. Тим самим ми будемо |
||||||||||||||||
озглядати |
|
|
|
|
|
ÿê |
|
|
квантовихосциляторiв |
|
|||||||
ляторiвен етичних рiвнiв хвиль |
уонiан,сукупнiстькцiй. Це акорнийж дасть змîãó |
||||||||||||||||
ââåсти поняелектромагнiтнео она. |
|
явного вигляду операто- |
|||||||||||||||
iç |
. |
Задача поляга¹ |
знахполеджен |
||||||||||||||
|
|
|
величин п ля (гамiль |
|
âåê |
|
|
|
|
|
|
||||||
напруженос |
|
ðè÷í ãî é ìàãíiò ого полiв), обчисленнiпотенцiал,й |
|||||||||||||||
Для виконання |
цi¹¨ програовихдi¹мо |
àêèì ÷èí |
. Ïðè âiäñóò |
|
|||||||||||||
ля, його ск лярний потенцiал ì |
жна вибрати ðiâíèì |
нулевi. Век- |
|||||||||||||||
стi зарядiв |
струмiв, тобто для вiльного електр |
агнiтного по |
|
||||||||||||||
торний потенцiал A = A(r, t)поперечностiякункцiя простоðîвих координат
r i ÷àñó t задово ьня¹ умову |
ïîëÿ |
div A = 0. |
471 |
