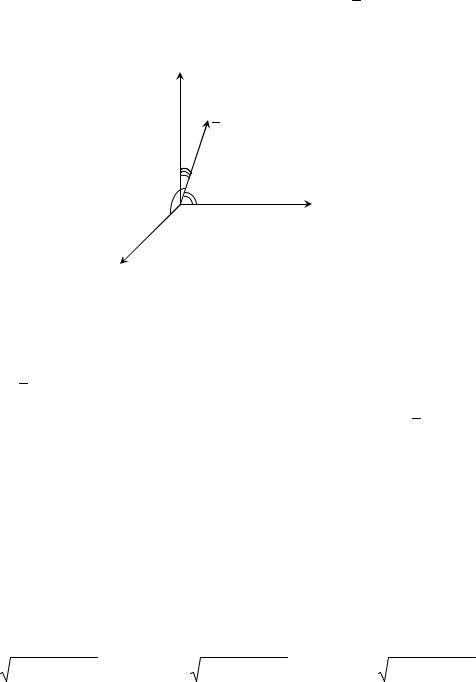
§10. Направляющие косинусы вектора
Обозначим буквами , , — углы наклона вектора a к осям Ox, Oy и Oz со-
ответственно (рис. 16).
z
a
|
|
|
y |
||
|
||
х |
|
|
|
Рис. 16 |
Определение 10.1. Числа cos , cos , cos называются направляющими коси-
нусами вектора a .
Пусть относительно прямоугольного декартова базиса вектор a имеет коорди-
наты |
a |
{a1 , a2 , a3}. По теореме 9.2 |
прOx |
a |
|
|
a1 , |
прOy |
a |
a2 , |
прOz |
a |
a3 . Учитывая |
|||||||||||||||||||||||||||
формулы (9.1), получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
a1 |
|
|
|
|
cos , |
a2 |
|
|
|
|
|
|
cos , |
a3 |
|
|
|
|
|
|
cos . |
|
|
(10.1) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
a |
a |
a |
|
|
|||||||||||||||||||||||||||||||
|
Подставляя выражение длины вектора |
|
|
из равенства (9.2), находим следую- |
||||||||||||||||||||||||||||||||||||
|
a |
|||||||||||||||||||||||||||||||||||||||
щие выражения для направляющих косинусов вектора: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
cos |
|
a1 |
|
, |
|
cos |
|
|
|
|
|
|
|
|
|
|
a2 |
|
, |
|
cos |
|
|
|
a3 |
|
. (10.2) |
||||||||||||
|
a2 |
a2 |
a2 |
|
|
a2 |
a2 a2 |
|
|
a2 |
a2 |
a2 |
||||||||||||||||||||||||||||
|
|
|
1 |
2 |
3 |
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
|
||||||||
Возводя в квадрат обе части каждого из равенств (10.2) и складывая полученные результаты, находим
(10.3)
т.е. сумма квадратов направляющих косинусов любого вектора равна единице.
30
Так как вектор однозначно определяется своими координатами, то из формулы (10.1) следует, что он также однозначно определяется своей длиной и направляющими косинусами.
Замечание. Из равенств (10.1) следует, что координаты единичного вектора совпадают с его направляющими косинусами, т.е. e {cos ,cos ,cos } .
§11. Скалярное произведение векторов
Определение 11.1. Скалярным произведением двух векторов a и b называется число, равное произведению длин этих векторов на косинус угла между ними.
Скалярное произведение обозначается (a,b) , или a b , или пишут просто a b .
Таким образом, по определению |
|
a b a b cos . |
(11.1) |
Замечание. Под углом между векторами a и b понимается наименьший из двух углов, образуемых этими векторами при совмещении их начал, т.е. 0 .
^
Иногда для обозначения угла между векторами a и b пишут (a , b) . Замечание. В случае если один из векторов-сомножителей равен нулю, то и
скалярное произведение равно нулю.
Если в формулу скалярного произведения (11.1) подставить выражение проек-
ции вектора a на вектор b из равенства (9.1), то можно получить еще одну формулу скалярного произведения
|
|
|
|
|
|
|
|
|
a |
|
|
b |
|
|
a |
|
|
|
пр |
|
|
b |
|
|
(11.2) |
|||
|
|
|
|
|
|
|
|
|
|
|
a |
|||||||||||||||||
или |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
прb |
|
. |
(11. 2 ) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
a |
b |
b |
a |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Свойства скалярного произведения |
|
|||||||||||||||||||
1) |
|
|
|
|
|
|
|
(коммутативность); |
|
|||||||||||||||||||
a |
b |
b |
a |
|
||||||||||||||||||||||||
31
2) |
a |
( |
b |
|
c |
) |
a |
|
b |
|
|
a |
|
c |
(дистрибутивность); |
||||||||||||||||||||
|
|
|
|
|
3) ( |
|
) |
|
|
|
( |
|
) ( |
|
|
|
), |
R ; |
|||||||||||||||||
a |
b |
a |
b |
a |
b |
||||||||||||||||||||||||||||||
4) |
скалярное произведение |
вектора на себя равно квадрату его длины: |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|||||||||||||||||||||||||
|
a |
|
a |
|
a |
|
0 ; |
|
|||||||||||||||||||||||||||
5) скалярное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны, т.е. a b 0, a 0 и b 0 a b .
Свойства 1, 3-5 непосредственно следуют из определения11.1 исвойствкосинуса. Докажем свойство 2.
Учитывая формулу (11.2) и свойства проекций, получим
a (b c) a прa (b с) a (прa b прa с) a прa b a прa с a b a c.
Замечание. По аналогии с операцией умножения на множестве чисел в случае
скалярного умножения вектора на себя будем писать a2 вместо a a . На практике удобно использовать формулу для нахождения длины вектора, которая легко получается из свойства 4:
|
|
|
2 . |
(11.3) |
|
||||
a |
a |
Определение 11.2. Два ненулевых вектора a и b называются ортогональными, если их скалярное произведение равно нулю.
Теорема 11.1 (координатное представление скалярного произведения). Если векторы a и b относительно ортонормированного базиса {i, j, k } заданы своими ко-
ординатами, т.е. a {a1, a2 , a3}, b {b1,b2 ,b3} , то скалярное произведение векторов a
и b равно сумме произведений соответствующих координат этих векторов, т.е.
|
|
|
|
a1 b1 a2 b2 |
a3 b3 . |
(11.4) |
|||
|
a |
b |
|||||||
Доказательство. Запишем разложения |
векторов |
|
и |
|
по базису: |
||||
a |
b |
||||||||
a a1i a2 j a3 k , b b1i b2 j b3 k . Найдем скалярное произведение этих векторов a b (a1i a2 j a3 k) (b1i b2 j b3 k) a1 b1(i i) a1 b2 (i j) a1 b3 (i k)a2 b1( j i) a2 b2 ( j j) a2 b3 ( j k) a3 b1(k i) a3 b2 (k j) a3 b3 (k k).
32
Так как i |
j |
|
k |
и |
i |
|
j |
|
|
|
k |
|
1, то по определению скалярного произведения |
||||||||||||||||||
имеем: i i |
|
|
|
|
|
|
|
1, |
|
i |
|
i |
|
|
|
|
|
0 . Учитывая эти равенства и свойство |
|||||||||||||
j |
j |
k |
k |
|
j |
k |
j |
k |
|||||||||||||||||||||||
коммутативности скалярного произведения, окончательно находим: |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a1 b1 a2 b2 a3 b3 .▲ |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
b |
|||||||||||
Следствие 11.1. Скалярные произведения вектора |
|
, заданного в ортонорми- |
|||||||||||||||||||||||||||||
a |
|||||||||||||||||||||||||||||||
рованном базисе {i, j, k } координатами a {a1, a2 , a3}, на соответствующие базисные векторы равны координатам этого вектора, т.е.
|
|
|
|
|
|
a |
i a1, |
|
a |
|
j |
a2 , |
a |
|
k |
a3. |
|
Следствие 11.2. |
|
|
|
|
a2 |
a2 |
a2 . |
|
|
|
|
||||||
|
a |
|
|
|
|
|
|||||||||||
|
|
|
1 |
2 |
3 |
|
|
|
|
|
|||||||
Это непосредственно следует из формул (11.3) и (11.4).
Следствие 11.3. Косинус угла между ненулевыми векторами a и b , заданными в базисе { i, j, k } координатами a {a1, a2 , a3}, b {b1,b2 ,b3} , вычисляется по формуле
|
|
|
|
|
|
|
|
|
|
|
|
|
a1 b1 a2 b2 a3 b3 |
|
|
|
|
|
||||
cos |
|
|
a |
b |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
. |
(11.5) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
a12 a22 a32 b12 b22 b32 |
|||||||||||
|
|
|
b |
|
|
|||||||||||||||||
a |
|
|
||||||||||||||||||||
Что непосредственно следует из формул (11.1), (11.4) и следствия 11.2. |
|
|
|
|
|
|||||||||||||||||
Замечание. Косинусы углов |
|
|
|
между вектором |
|
и базисными векторами i, |
|
, |
|
|
||||||||||||
|
|
|
a |
j |
k |
|||||||||||||||||
и есть направляющие косинусы вектора a , о которых шла речь в определении 10.1. При подстановке координат векторов a {a1, a2 , a3}, i {1,0,0}, j {0,1,0}, k {0,0,1} в формулу (11.5) получаются формулы для нахождения направляющих косинусов вектора a , аналогичные равенствам (10.2).
Следствие 11.4. Проекция вектора a на направление, определяемое вектором b , находится по формуле
пр |
|
|
|
|
a |
|
b |
|
a1 b1 a2 b2 a3 b3 . |
(11.6) |
|
|
a |
||||||||||
|
|||||||||||
|
|
|
|
|
|
|
|||||
b |
|
|
|
b |
|
|
b12 b22 b32 |
|
|||
|
|
|
|
|
|
|
|
||||
Всправедливости формулы легко убедиться, используя формулы (11.2), (11.4)
иследствие 11.2.
Геометрический смысл скалярного произведения. Угол между двумя ненуле-
выми векторами острый (тупой), если скалярное произведение этих векторов есть
33