ГЛАВА 2 РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ

ПО ТЕМЕ «ВЕКТОРНАЯ АЛГЕБРА»

1. Векторы: длина вектора, координаты вектора, направляющие косинусы вектора

Задача1. Найтикоординатыимодульвектора AB , еслиА(2, –1, 3), В(–9, 3, 7).

Решение. Найдем координаты вектора AB , вычитая из координат конца координаты начала, т.е. AB {x2 x1 , y2 y1 , z2 z1} { 11, 4, 4}. Затем воспользуемся формулой(9.2) длянахождениядлинывектора:

a a12 a22 a32

ивычислимдлинувектора AB :

AB ( 11)2 42 42 121 16 16 153 .

Ответ: AB 153 .

Задача 2. Определить точку В, с которой совпадает конец вектора a {5, 1, 8}, еслиегоначалосовпадаетсточкойА(–3, 2, 4).

Решение. По условию задачи AB a . Записав данное векторное равенство в координатной форме, получим:

Ответ: B(2, 1, 12).

44

Задача 3. Дана длина вектора a : a 5 и углы, которые вектор образует с коор-

динатными осями: 600 ; 900 ; 1500 . Вычислить проекции вектора на координатные оси.

Решение. Проекции вектора на координатные оси равны, согласно теореме 9.2, координатамданноговектора. Поформулам(10.1) найдем

Ответ: a {52 , 0, 5 23}.

Задача4. Вычислитьнаправляющиекосинусывектора a {12, 3, 4}.

Решение. Направляющие косинусы вектора можно рассчитать, воспользовавшись формулами(10.2)

Задача 5. Может ли вектор составлять с координатными осями следующие углы:

900 , 1200 , 300 ?

Решение. Если , и – углы, которые составляет вектор с координатными осями, тонаправляющиекосинусывекторадолжныудовлетворятьусловию:

cos2 cos2 cos2 1.

Проверим выполнение этого условия для данных углов:

cos2 900 cos2 1200 cos2 300 0 14 34 1.

45

Так как равенство выполнилось, то вектор может составлять с координатными

данныеизусловиязадачи. Получим:

cos2 cos2 600 cos2 1350 1 .

Заменяякосинусыуглов и наихтабличныезначения, выразим

Ответ: 600 или 1200 .

2. Линейные операции над векторами

Задача 1. Даны векторы a и b , причем a 13, b 19 и a b 24 . Вычислить

a b .

Решение. Выберем в пространстве точку А и отложим от нее векторы a и b так, чтобы a AB, а b AD . Построим на векторах a и b параллелограмм ABCD, тогда одна направленная диагональ параллелограмма будет являться суммой векторов a и b , а другая – разностью, т.е. a b AC, а a b DB (см. рис.19).

46

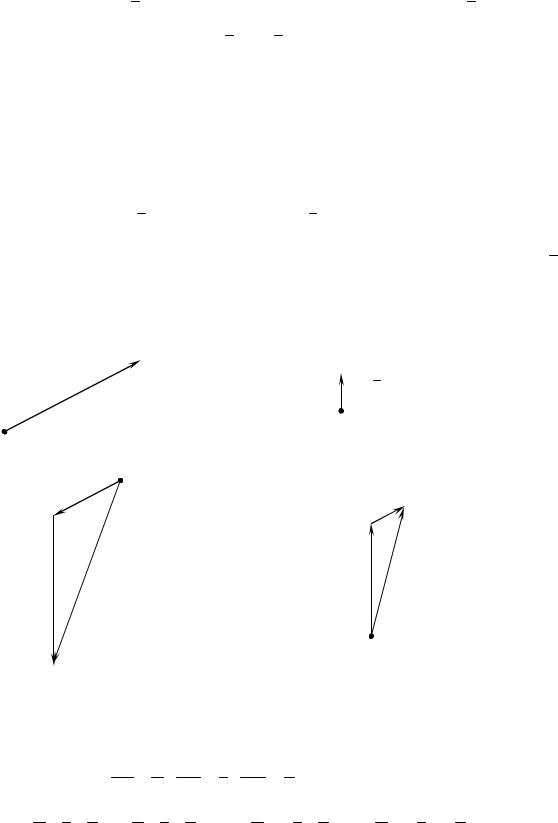
Решение. Согласно определению (2.2) произведения вектора на число, для того, чтобы построить вектор 2a , нужно увеличить в 2 раза длину вектора a и построить вектор соноправленный данному, т.е. a 2a (см. рис. 21, 1). В пункте 2 длину век-

совмещая конец вектора a с началом вектора 2b , по правилу треугольника сложе-

ния векторов найдем их сумму. Аналогично рассуждая, найдем сумму векторов 12 a и

Рис. 21

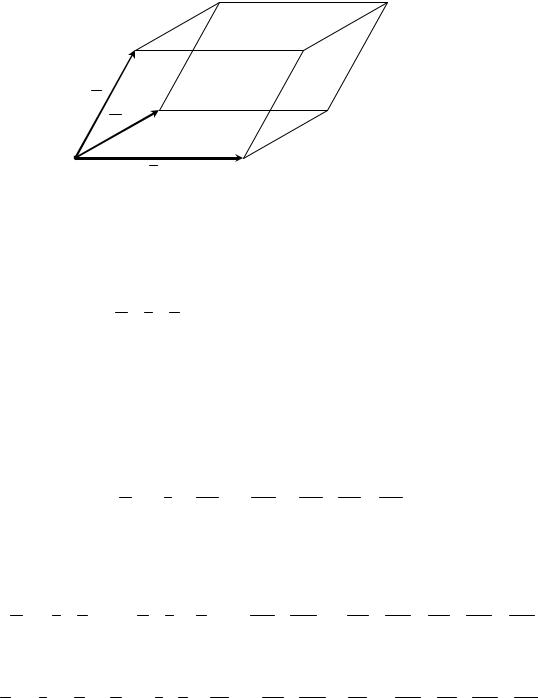
Задача 3. В параллелепипеде ABCDA B C D (см. рис. 22) заданы векторы, совпадающие с его ребрами: AB m, AD n, AA p . Построить каждый из следующих

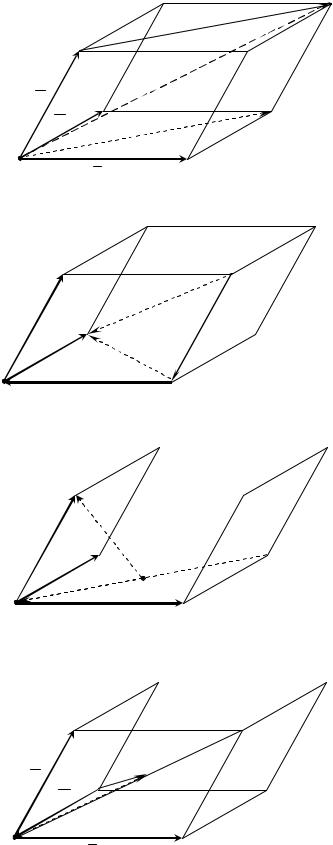
векторов: 1) m n p ; 2) m n p ; 3) 12 m 12 n p ; 4) m 12 n 12 p .

48

Задача 5. При каком значении m и l векторы a mi 3 j 4k и b 2i l j 8k коллинеарны.

Решение. Для коллинеарных векторов справедливо следствие 7.2, в котором говорится, что коллинеарные векторы имеют пропорциональные координаты, т. е.

a1 a2 a3 . b1 b2 b3

Подставляя в последние равенства координаты данных векторов, имеем:

m3 4 .

2 l 8

Откуда найдем: 8m= –8 m= –1; 4l=24 l=6.

Ответ: при m= –1, l=6 векторы a и b коллинеарны.

Задача 6. Даны точки A(1, 8, 5), B(3, 5, 12), C(8, 4, 0) и D(14, –5, 21). Прове-

рить, что векторы AB и CD коллинеарны; установить, какой из них длиннее другого и во сколько раз, как они направлены — в одну или в противоположные стороны.

Решение. Найдемкоординатывекторов AB и CD по формуле (9.3):

AB {3 1,5 8,12 5} {2, 3, 7}, CD {14 8, 5 4, 21 0} {6, 9, 21}.

Проверим, будут ли пропорциональны координаты рассматриваемых векторов, т.е. проверимвыполнениеравенств

51

CD втриразадлиннеевектора AB .

Задача 7. Дано разложение вектора a по базису {i, j, k}: a 2i 3 j 7k .

Определить разложение по этому же базису вектора b , параллельного вектору a и противоположного с ним направления, при условии, что длина вектора b равна

12 2 .

Решение. Так как векторы a и b коллинеарны, то b k a . Таким образом, ко-

ординаты вектора b пропорциональны координатам вектора a , т.е. b {2k, 3k, 7k} .

Зная координаты и длину вектора b , составим и решим уравнение: (2k)2 ( 3k)2 (7k)2 12 2 ,

4k 2 9k 2 49k 2 12 2,

62k 2 12 2 , 6 2k 12 2 , k 2 .

По условию a b , следовательно k 0 , а значит в нашем случае k 2 . Таким образом, b { 4, 6, 14}.

Ответ: b 4i 6 j 14k .

Задача 8. Найти орт вектора a {3, 6,10}.

Решение. Координаты орта вектора a находятся по формуле:

52

странства образуют базис, достаточно убедиться, что они некомпланарны. Это означает, согласно следствию 7.3, что определитель 3-го порядка, составленный из координат этих векторов, должен быть отличен от нуля. Для нашего случая имеем:

Таким образом, векторы a, b и с можно взять в качестве базиса трехмерного

пространства, а вектор d , согласно теореме 5.3, представить в виде: d a b c .

Коэффициенты в разложении и есть координаты вектора d относительно данного базиса. Для того чтобы их найти, воспользуемся теоремой 7.2 и перепишем векторное равенство в координатной форме

Получили систему трех уравнений с тремя неизвестными. Решая ее методом Гаусса, найдем

53