
- •ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
- •ОГЛАВЛЕНИЕ
- •ВВЕДЕНИЕ
- •Глава 1 ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
- •§1. Понятие вектора*
- •§2. Линейные операции над векторами
- •§3. Понятие линейного пространства
- •§4. Линейная зависимость и независимость системы n векторов
- •§5. Примеры линейно зависимых и линейно независимых систем векторов
- •§6. Базис. Координаты* вектора в базисе
- •§7. Действия над векторами в координатах
- •§8. Аффинная и прямоугольная декартова системы координат
- •§9. Проекция вектора на ось
- •§10. Направляющие косинусы вектора
- •§11. Скалярное произведение векторов
- •§12. Евклидово пространство*: основные понятия
- •§13. Векторное произведение векторов
- •§14. Смешанное произведение векторов
- •§15. Двойное векторное произведение
- •1. Векторы: длина вектора, координаты вектора, направляющие косинусы вектора
- •2. Линейные операции над векторами
- •3. Скалярное произведение векторов
- •4. Векторное произведение векторов
- •5. Смешанное произведение векторов
- •ТИПОВОЙ ВАРИАНТ КОНТРОЛЬНОЙ РАБОТЫ ПО ТЕМЕ ВЕКТОРНАЯ АЛГЕБРА
- •БИБЛИОГРАФИЧЕСКИЙ СПИСОК

x |
x1 x2 |
, |
y |
y1 y2 |
, |
z |
z1 z2 |
. |
(8. |
|
) |
|
2 |
2 |
2 |
||||||||||
3 |
Замечание. На плоскости (в двумерном пространстве) можно также задать прямоугольную систему координат Oxy. С помощью введенной системы координат любую точку или ее радиус-вектор можно представить парой чисел (x, y). Все соотношения, полученные нами ранее для координат векторов и точек трехмерного пространства, будут справедливы и на плоскости с той лишь разницей, что из них нужно всюду убрать третью координату z. Аналогичные рассуждения можно повторить и для произвольной прямой (одномерного пространства).
§9. Проекция вектора на ось
Определение 9.1. Осью называется прямая с лежащим на ней единичным вектором (ортом), задающим положительное направление на прямой.
На рисунке ось будем изображать в виде направленной прямой. Пусть в пространстве задана ось l и точка А, не принадлежащая оси.
Определение 9.2. Основание перпендикуляра, опущенного из точки А на пря-
мую l, точка A' называется проекцией (ортогональной проекцией) точки на ось.
В случае, если точка А принадлежит оси l, то проекция точки на ось совпадает с самой точкой А.
Пусть задан некоторый вектор a AB . Находя проекции начала и конца вектора a на ось l, получим вектор a' A' B' , где A', B' — соответственно проекции точек А, В на ось l.
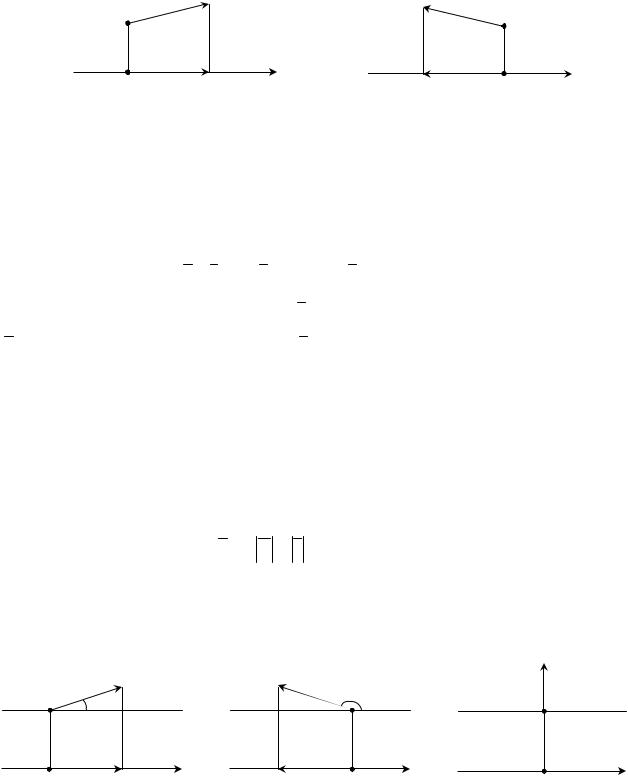
Определение 9.3. Проекцией вектора a на ось l будем называть положительное число, равное a' , если вектор a' и ось l направлены одинаково (см. рис. 12) и отрица-
тельное число a' , если вектор a' и ось l направлены противоположно (см. рис. 13).
26
|
|
|
a |
|
|
|
В |
|
|
|
|
|
|
|
|
В |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
||||||
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
a |
|
|
|
|
|
l |
|
|
|
|
|
|
a |
l |
||||||||
А' |
В' |
|
|
|
|
|
|
|
B' |
|
|
|
|
|
A' |
|||||||||
Рис. 12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 13 |
|
|||||||
Проекцию вектора |
|
на |
ось l |
будем обозначать прl |
|
|
|
. Таким образом, соглас- |
||||||||||||||||
a |
a |
|||||||||||||||||||||||
но определению прl |
|
|
|
|
|
|
|
или прl |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
a |
|
a |
|
a |
|
a |
. |
|
|
|
|
|
|
|
||||||||||
Замечание. Если a 0 или a l , то прl a 0 .
Теорема 9.1. Проекция вектора a на ось l равна произведению длины вектора a на косинус угла между вектором a и осью l, где под углом понимается наименьший из двух углов, образуемых вектором и осью.
Таким образом,
прl |
|
|
|
|
cos |
(0 ) . |
(9.1) |
a |
a |
||||||
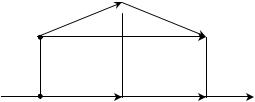
Доказательство. В зависимости от величины угла |
возможны следующие |
||||||
случаи (рис. 14):
1. Если 900 , то прl a a a cos .
2. Если |
900 1800 , то прl |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos( ) |
|
|
cos . |
|
|
|
|||||||
a |
a |
a |
a |
|
|
|
|||||||||||||||||||||||||
3. Если |
900 , то пр |
|
0 |
|
|
|
|
|
cos . ▲ |
|
|
|
|||||||||||||||||||
a |
|
a |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
a |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
a |
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
l |
|
|
|
|
l |
|
|
l |
||||||||||||||||||
Рис. 14
27
Следствие 9.1. Проекция вектора на ось есть число положительное, если уголмежду вектором и осью острый, и отрицательное, если угол тупой. Если уголпрямой, то проекция вектора на ось равна нулю.
Следствие 9.2. Проекции равных векторов на одну и ту же ось равны между
собой.
Свойства проекций векторов на ось
1) прl |
|
прl |
|
прl ( |
|
|
|
|
|
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
a |
b |
a |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
2) прl ( |
|
) прl |
|
, |
|
R. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
a |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Доказательство: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) обозначим c a b . Рассмотрим прl c |
|
|
|
|
|
|
|
a |
|
|
|
прl |
a прl b (рис.15); ▲ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
c |
|
|
|
b |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
a |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2) в зависимости от знака возможны следующие случаи: |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
прl ( |
|
|
|
|
по теореме 9.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos прl |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
a) 0 : |
a |
) |
|
|
|
a |
|
|
cos |
a |
|
a |
. |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
прl ( |
|
|
|
по теореме 9.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( cos ) прl |
|
|
||||||||||||||||||||||||||
b) 0 : |
a |
) |
|
|
|
a |
|
cos( ) |
a |
|
a |
. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
прl ( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
см. замечание копр.9.3 |
0 прl |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
c) 0 : |
a |
) прl (0) |
|
|
|
|
|
|
|
a |
. ▲ |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
Таким образом, линейные операции над векторами сводятся к соответствующим линейным операциям над проекциями этих векторов.
Замечание. Все рассуждения, приведенные выше, будут также справедливы, если вместо оси l рассматривать произвольный ненулевой вектор. Проекцию (ортого-
28
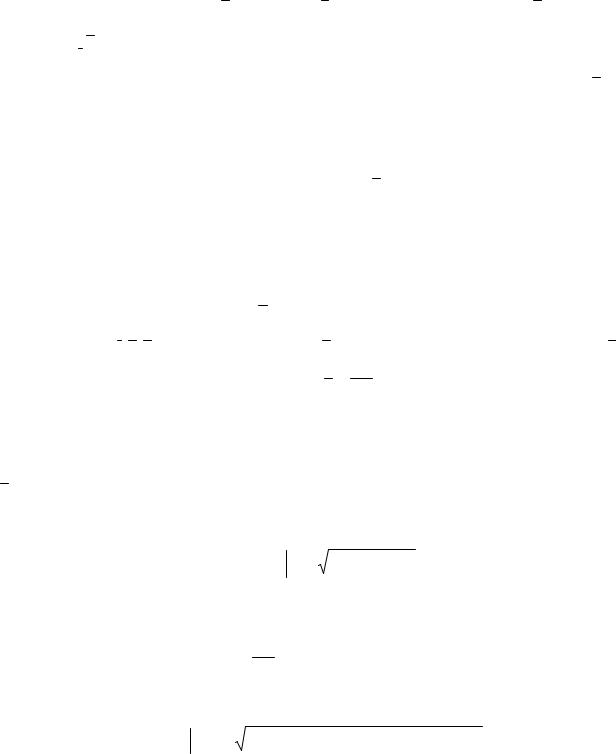
нальную проекцию) вектора a на вектор b (на направление вектора b ) будем обо-
значать прb a .
Теорема 9.2. Декартовы прямоугольные координаты a1 , a2 , a3 вектора a рав-
ны соответственно проекциям этого вектора на оси Ox, Oy и Oz.
Можно дать еще одно определение координат вектора.
Определение 9.4. Координатами вектора a в прямоугольной декартовой системе координат Oxyz называются проекции этого вектора на соответствующие координатные оси.
Рассмотрим задачу о нахождении длины вектора по его координатам.
Задача. Пусть дан вектор a , который относительно прямоугольного декар-
тового базиса {i, j, k} имеет координаты: a {a1 , a2 , a3}. Найдем длину вектора a .
Решение. Найдем проекции вектора a OA на координатные оси и обозначим их OA1,OA2 иOA3 . Согласно теореме 9.2, OA1 a1 , OA2 a2 , OA3 a3 . Построим пря-
моугольный параллелепипед так, что его три измерения равны OA1,OA2 иOA3 . Вектор
a в построенном параллелепипеде совпадает с диагональю (см. рис. 9). Так как квадрат диагонали в прямоугольном параллелепипеде равен сумме квадратов его сторон, то
|
|
a2 |
a2 |
a2 . |
(9.2) |
a |
|||||
|
1 |
2 |
3 |
|
|
Таким образом, длина вектора равна корню квадратному из суммы квадратов координат этого вектора.
Замечание. Длина вектора AB , где A(x1 , y1 , z1 ) , B(x2 , y2 , z2 ) , согласно формулам (8.2), (9.2), находится по формуле
|
(x |
|
x )2 |
( y |
|
y )2 |
(z |
|
z )2 . |
(9.3) |
AB |
2 |
2 |
2 |
|||||||
|
|
1 |
|
1 |
|
1 |
|
29
