
Задачи Крюкова / Кинетика 3
.pdf
Задача 1.
Зависимость скорости реакции от температуры выражается уравнением Аррениуса:
= 2
Или в логарифмической форме:
= − ∙ 1,
где k – константа скорости, А – предэкспоненциальный множитель, Еа –
энергия активации.
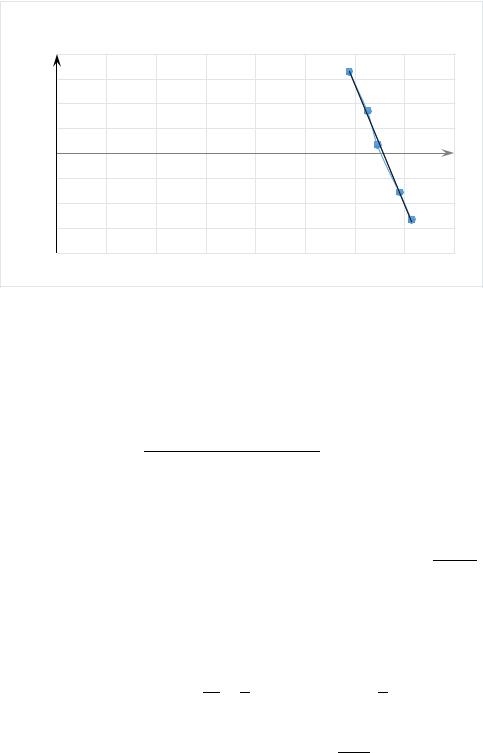
Используем графический способ, который сводится к построению линейной
|
1 |
|
|
|
|
зависимости ln k = f( |
|
) с = − |
|
и отсекаемым отрезком ln А на оси |
|
|
|
||||
|
|
|
ординат, из которых определяют предэкспоненциальный множитель (А) и
энергию активации (Ea) реакции.
|
|
|
|
ln k = f(T) |
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1/Т, К^-1 |
k |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
ln |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0,0005 |
0,001 |
0,0015 |
0,002 |
0,0025 |
0,003 |
0,0035 |
0,004 |
|
-2 |
|
|
|
|
|
|
|
|
|
-4 |
|
|
|
|
|
|
|
|
|
-6 |
|
|
|
|
y = -19071x + 62,675 |
|
||
|
|
|
|
|
|
|
|
|
|
|
-8 |
|
|
|
|
|
|
|
|
Тангенс угла находим как отношение противолежащего катета выбраноого |
|||||||||
треугольника к прилежащему. Учитываем, что = |
− : |
|
|||||||
|
|
= − |
|
6,590 + 3,112 |
|
= −19136,1 |
|
||
|
|
0,002941 − 0,003448 |
|
||||||
Следовательно, энергия активации равна: |
|
|
|
|
|||||
Дж Еа = − = −(−19136,1 8,312) = 159059,3(моль)
Теперь, пользуясь табличными данными можем найти предэкспоненциальный множитель (А), используя уравнение Аррениуса:
= − ∙ 1 = + ∙ 1
1 −3,112 = ln − 19136,1 ∙ 290
= 2,023 ∙ 1027(мин−1)
Теперь рассчитаем время полупревращения. Так как размерность константы дана в [мин-1], сделаем вывод, что у нас реакция первого порядка, поэтому:
1 |
= |
2 |
|
⁄ |
|
||
|
|||
2 |
|

Для дальнейших расчетов необходимо найти константу реакции при Т=300 К.
Выражаем константу из уравнения Аррениуса:
= ∙ −
159059,3
= 2,023 ∙ 1027 ∙ −8,312∙300 = 0,40146 (мин−1)
21⁄2 = 0,40146 = 1,726 (мин)
Ответ: Еа = 159059,3 (Дж/моль); А = 2,023 *1027 (мин-1); t1/2=1,726 (мин)
Задача 2.
Для начала определим порядок данной реакции. Для этого можем воспользоваться аналитическим интегральным методом Оствальда-Нойесса,
который основан на зависимости времени полупревращения от начальной концентрации исходного вещества (в нашем случаем вместо концентраций можно использовать давления, данные в условии):
|
|
1⁄2(2) |
|
|
1⁄2(2) |
|
|
|
73,2 |
|
|
|
1⁄2(1) |
|
1⁄2(1) |
|
|
|
|
||||
= |
|
+ 1 = |
|
|
+ 1 = |
62,4 |
+ 1 = 2 |
||||
|
|
|
|
|
|
|
750 |
||||
|
|
0(1) |
|
|
|
0(1) |
|
|
|
640 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||
|
|
0(2) |
|
|
|
0(2) |
|
|
|
|
|
Мы определили, что дана реакция второго порядка. Таким образом константу скорости можем выразить из следующей формулы:

1 |
|
= |
1 |
→ = |
|
|
1 |
|
= |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||
⁄ |
|
|
1⁄ |
|
1⁄ |
0 |
|||||||
|
2 |
|
0 |
|
|
|
0 |
|
|
||||
|
|
|
|
|
|
2 |
|
|
|
2 |
|
||
Для расчета за начальное давление берем 750 мм. рт. ст. и время
полупревращения, равное 62,4 мин:
1= 62,4 ∙ 750 = 2,136 ∙ 10−5 ((мин ∙ мм. рт. ст)−1)
Ответ : n = 2; k = 2,136 ∙ 10−5 ((мин ∙ мм. рт. ст)−1)
Задача 3.
Все реакции радиоактивного распада являются реакциями первого порядка.
Время полупревращения подчиняется следующей формуле:
21⁄2 =
Выразим из уравнения выше константу скорости химической реакции:
= |
2 |
= |
2 |
|
= 9,72 ∙ 10−10(лет−1) |
|
|
7,13∙10 |
8 |
||||
|
1 |
|
|
|
|
|
|
⁄ |
|
|
|
||
|
|
2 |
|
|
|
|
Теперь найдем время, за которое содержание 235урана в образце уменьшилось на 0,05%.
= 0 −
Выражаем t:
= 1 0
Находим концентрацию после уменьшения содержания 235урана на 0,05%:
= (1 − 0,05) 0
Рассчитываем время:
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
1 |
= 5,28 ∙ 107 |
|
= |
|
|
0 |
= |
|
|
0 |
|
= |
|
∙ |
|
(лет) |
|
|
|
|
(1−0,05) |
0 |
9,72∙10−10 |
1−0,05 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ:k = 9,72 ∙ 10−10(лет−1); t = 5,28 ∙ 107(лет)
