Sb95706

МИНОБРНАУКИ РОССИИ

–––––––——————————–––––––

Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В. И. Ульянова (Ленина)

–––––––——————————–––––––

РАЗРАБОТКА И АНАЛИЗ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ГИРОСКОПИЧЕСКОГО ПРИБОРА ДЛЯ СИСТЕМ АВТОНОМНОЙ НАВИГАЦИИ

И УПРАВЛЕНИЯ

Учебное пособие

Санкт-Петербург Издательство СПбГЭТУ «ЛЭТИ»

2017

1

УДК 531.383(07) + 681.783.322.3(07) ББК В213.33я7 + К948я7

Р17

Авторы: А. М. Боронахин, Л. Н. Подгорная, А. Н. Ткаченко,

Р. В. Шалымов

Р17 Разработка и анализ математической модели гироскопического прибора для систем автономной навигации и управления: учеб. пособие. СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2017. 48 с.

ISBN 978-5-7629-2056-8

Рассмотрены способы получения дифференциальных уравнений движения механических систем и их применение для составления математических моделей гироскопических приборов. Значительное внимание уделено особенностям использования гироскопических приборов в составе систем автономной навигации и управления движением.

Предназначено для подготовки бакалавров и магистров, обучающихся по направлениям12.03.01,12.04.01«Приборостроение»,кзанятиямпо дисциплинам «Аналитическая механика», «Математические модели навигационных приборов», «Инерциальные навигационные системы».

УДК 531.383(07) + 681.783.322.3(07) ББК В213.33я7 + К948я7

Рецензенты: кафедра инерциальных навигационных систем университета ИТМО; канд. техн. наук Ю. А. Литвиненко (АО «Концерн ЦНИИ “Электроприбор”»).

Утверждено редакционно-издательским советом университета

в качестве учебного пособия

2

ВВЕДЕНИЕ

Гироскопические приборы находят широкое применение в качестве построителей инерциальной системы отсчета на подвижном объекте или измерителей его кинематических характеристик, как в качестве самостоятельных датчиков, так и в составе систем автономной навигации и управления движением.

Используемая в настоящее время гироскопическая техника может функционировать на базе различных физических принципов. Свое применение находят оптические, твердотельные, вибрационные гироскопы и системы на их основе. Однако, несмотря на большое количество разновидностей этих систем, классические роторные гироскопы с кардановым подвесом все еще активно эксплуатируются в составе систем навигации и управления движением различных подвижных объектов.

Структура настоящего учебного пособия предусматривает его использование в образовательном процессе по нескольким дисциплинам, последовательно изучаемым студентом.

Первая глава предлагается к изучению в рамках курса «Аналитическая механика» и посвящена получению дифференциальных уравнений движения механических систем. Рассмотрены методы получения уравнений тремя способами с использованием: теоремы о движении центра масс механической системы (основного уравнения динамики) и теоремы об изменении кинетического момента механической системы (динамических уравнений Эйлера), принципа Германа–Эйлера–Даламбера, уравнения Лагранжа второго рода.

Вторая глава содержит сведения из курса «Математические модели навигационных приборов» и посвящена использованию описанных в первой главе методов для получения математической модели гироскопического прибора на примере трехстепенного астатического гироскопа (ТАГ). В конце главы приводится анализ полученных уравнений движения.

Третья глава предлагается к изучению в рамках курса «Инерциальные навигационные системы» и посвящена особенностям применения гироскопических приборов в составе систем автономной навигации и управления движением. Рассмотрены основы построения инерциальных навигационных систем (ИНС). Подробно представлено функционирование ИНС полуаналитического типа.

3

Таким образом, настоящее пособие позволяет связать в единое целое информацию, получаемую студентами в процессе изучения трех дисциплин, что должно способствовать систематизации приобретенных ими знаний и формированию междисциплинарных компетенций.

1. ПОЛУЧЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ДВИЖЕНИЯ МЕХАНИЧЕСКИХ СИСТЕМ

Если механизм отклонить от положения равновесия, то под действием заданных сил он придет в движение. Для исследования движения механических систем необходимо составить дифференциальные уравнения движения.

Дифференциальные уравнения движения твердых тел и механических систем могут быть получены с использованием различных методов. В основе каждого из таких методов лежит некоторая теорема или принцип динамики. Выбор метода, как правило, определяется удобством вычислений в каждом конкретном случае. Среди основных методов, применяемых для получения уравнений движения в гироскопической технике, можно выделить: динамические уравнения Эйлера, принцип Даламбера и уравнения Лагранжа второго рода.

Независимо от используемого метода получения дифференциальных уравнений движения механической системы, необходимо определить для нее число степеней свободы и выбрать обобщенные координаты (независимые между собой параметры, однозначно определяющие положение системы в пространстве),соответствующиеэтимстепенямсвободы.Отвыбораобобщенных координат напрямую зависит сложность вычислений.

1.1. Основное уравнение динамики и динамические уравнения Эйлера

Из кинематики известно, что в общем случае движение твердого тела может быть представлено как совокупность поступательного движения вместе с некоторой точкой, принятой за полюс (при решении задач динамики за полюс обычно принимают центр масс тела C), и вращательного движения вокруг этого полюса, как вокруг неподвижной точки [1].

Исходя из вышесказанного, уравнения движения тел, входящих в состав механической системы, могут быть получены с использованием двух теорем: о движении центра масс и об изменении кинетического момента, характеризующих поступательную и вращательную составляющие движения, соответственно.

4

Основное уравнение динамики (второй закон Ньютона) гласит, что ускорение материальной точки пропорционально приложенной к ней силе и имеет одинаковое с ней направление. Обобщив этот закон для тела, получим выра-

жение, называемое теоремой о движении центра масс [2]: maC F E ,

где F E – главный вектор внешних сил, действующих на тело; m – масса тела; aC – ускорение центра масс тела.

Или в проекциях на неподвижные декартовы оси Oxgygzg:

вой системы координат; xgC , ygC , zgC – проекции ускорения центра масс на оси декартовой системы координат.

тральных осей инерции; x , y , z – проекции вектора угловой скорости тела

5

на оси связанной системы координат; x , y , z – проекции вектора углового ускорения тела на оси связанной системы координат; M xE , M yE ,M zE – проек-

ции главного момента внешних сил на оси Oxyz.

Выражения (1.2) позволяют получить дифференциальные уравнения сферического движения и носят название динамических уравнений Эйлера.

1.2. Принцип Германа–Эйлера–Даламбера

Принцип Германа–Эйлера–Даламбера – это общий метод, при помощи которого уравнениям динамики по форме придается вид уравнений статики [2].

Рассмотрим материальную точку i массой m, движущуюся под действием активных сил и сил реакций связи (в случае несвободной точки) с некоторым ускорением a . Тогда справедливой будет следующая запись (эквивалентная второму закону Ньютона):

вектор сил реакций связей, действующих на точку i; i ma – сила инерции

точки i (специально вводимая фиктивная сила).

Обобщение (1.3) для механической системы позволяет записать два выражения (для сил и моментов сил), имеющих вид [1]

где MO FiE – главный момент внешних сил, действующих на точку i, отно-

сительно точки O; MO FiI – главный момент сил реакций связей, действую-

щих на точку i, относительно точки O; MO i – момент силы инерции точки

i относительно точки O.

Для системы, подчиненной идеальным связям [суммы внутренних сил (реакций связей) и моментов внутренних сил равны нулю], (1.4) и (1.5) примут

относительно точки O.

1.3. Уравнение Лагранжа второго рода

Наиболее общий способ составления дифференциальных уравнений движения основан на уравнениях Лагранжа второго рода [3]. Для каждой обобщенной координаты уравнение Лагранжа имеет вид

где T – кинетическая энергия системы, выраженная через обобщенную координату q j иобобщенную скорость q j ; Q j – обобщенная сила; j – номер обоб-

щенной координаты (от 1 до k, где k – число степеней свободы механической системы); t – текущее время. Кинетическая энергия системы равна сумме кинетических энергий входящих в нее тел. Для определения кинетической энергии каждого тела используется формула, соответствующая виду его движения (поступательного, вращательного вокруг неподвижной оси, плоскопараллельного, сферического, либо общего случая движения).

Кинетическая энергия тела при поступательном движении определяется выражением [2]

T 12mv2 ,

где m – масса тела; ν – скорость какой-либо его точки.

При вращательном движении вокруг неподвижной оси имеем [2]:

T 12I 2 ,

гдеI – моментинерциителаотносительноосивращения;ω–угловаяскорость. Кинетическая энергия тела при плоскопараллельном движении складывается из кинетических энергий поступательного и вращательного движений

(вокруг неподвижной оси) и определяется выражением [2]

T 12mvC2 12IC 2,

7

где vC – скорость центра масс тела; IC – его момент инерции относительно

оси, проходящей через центр масс. Значения скоростей точек тел могут быть определены по их проекциям на декартовы оси координат:

нии x , y координатых, уточекдолжныбытьпредварительно выраженычерез обобщенные координаты q j .

При сферическом движении (вращательном вокруг неподвижной точки) имеем [2]:

T 12 I 2,

где I – момент инерции тела относительно мгновенной оси вращения; ω –

мгновенная угловая скорость вращения тела.

Кинетическая энергия тела в общем случае его движения складывается из кинетических энергий поступательного и сферического движений и определяется как [2]:

где vC – скорость центра масс тела; IC – его момент инерции относительно

мгновенной оси, проходящей через центр масс [4]. Значения скоростей точек тел могут быть определены по их проекциям на декартовы оси координат:

v x2 y2 z2.

Формула (1.9), если в качестве осей инерции используются главные центральные оси, примет вид [1]

где x, y, z – главные центральные оси инерции; Ix , I y , Iz – осевые моменты инерции тела, относительно главных центральных осей инерции; x , y , z –

проекции вектора угловой на оси x, y, z.

Каждая из обобщенных сил Q j , соответствующая обобщенной координате q j , может быть найдена как скалярный множитель перед приращением обобщенной координаты q j в выражении для элементарной работы [2]:

8

где Aj – элементарная работа задаваемых (активных) сил и моментов сил,

действующих на механизм.

Подсчет элементарной работы производится по формуле [2]

жения сил, M p – задаваемые моменты сил силы; p – возможные повороты

тел под действием моментов сил; i 1, 2, ...,n – количество точек системы; p 1, 2, ...,m – количество сил, действующих на систему.

В (1.12) все возможные перемещения выражаются через приращения обобщенных координат q j и после подстановки позволяют привести (1.12) к

виду (1.11), позволяющему найти Q j .

Другим способом определения обобщенной силы Q j является представ-

ление ее как суммы обобщенных сил, вызванных наличием в системе потенциальных и непотенциальных сил и моментов сил [2]:

Q j Qпотj Qнепотj .

При этом действие консервативных сил может быть получено [2]:

Qпотj q j ,

где П – потенциальная энергия.

Действие же неконсервативных сил, в общем случае определяется (1.11):

В частном случае, при учете диссипации энергии (также неконсервативное воздействие), для вычисления обобщенной силы используется функция Рэлея ( R ) [2]:

Qдисj R .

qj

После подстановки в (1.8) кинетической энергии T и обобщенной силы Q j получится обыкновенное дифференциальное уравнение относительно об-

общенной координаты q j , рассматриваемой как функция времени t. Это и

9

есть дифференциальное уравнение движения механизма. Полученное уравнение после перенесения всех его членов в левую часть будет иметь вид

Из (1.13) интегрированием находится закон движения механизма q j q j t .

Система таких уравнений по всем обобщенным координатам и является математической моделью механизма.

2. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ГИРОСКОПИЧЕСКОГО ПРИБОРА

2.1.Использование динамических уравнений Эйлера для получения математической модели ТАГ

Рассмотрим получение математической модели на примере трехстепенного астатического гироскопа (ТАГ), установленного на неподвижном основании с учетом массы кардановых колец. На основе такой схемы может быть построена гировертикаль (ГВ).

2.1.1. Кинематическая схема устройства

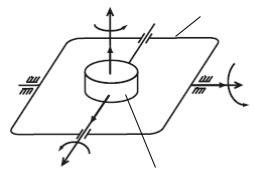
Кинематическая схема трехстепенного астатического гироскопа представлена на рис. 2.1.

2.1.2. Определение кинетического момента устройства

Вектор кинетического момента многомассовой системы представляет собой геометрическую сумму векторов кинетических моментов звеньев, входящих в систему: