
6552
.pdf81
или иной группы данных из всей их совокупности на итоговую оценку параметров. Например, если появились сомнения в точности первых десяти измерений, то их влияние можно ослабить, задав ω(k) <1, k ≤10.
Из условия минимума среднеквадратического отклонения Jir следует, что оценка параметров θɶr должна удовлетворять уравнениям:
dJir |
= 0,(i =1,2; r =1,2,....,N; s =1,2,...,m). |
(2.63) |
|
dθɶr |
|||
|
|
||
is |
|
|
Дифференцируя выражение (2.62), уравнения (2.63) запишем в виде:
r |
|
|
|
(k) ))= 0, |
|
|
∑ω(k) |
fi |
(k) (yi(k) − (θɶir , |
fi |
(i =1,2). |
(2.64) |
k=1
Символ здесь обозначает внешнее произведение векторов, так что для векторов a, b с компонентами ai , bj имеет место формула a b = C, Cij = ai bj ,
т. е. в результате внешнего умножения векторов получается матрица соответствующей размерности. Если один из сомножителей скаляр, то этот символ означает обычное умножение вектора на скаляр.
Для упрощения последующих преобразований соотношения (2.64) представим в следующем виде:
(Pir ) |
−1 |
|
r |
|
(k) yi(k), (i =1,2). |
|
|
θɶir = ∑ω(k) |
fi |
(2.65) |
|||
k=1
Всистемах (их две: при i =1 и при i = 2) линейных алгебраических урав-
нений (2.65) относительно неизвестных коэффициентов θɶir матрицы (Pir )−1 есть не что иное, как уже известные нам информационные матрицы Mi , в выражениях (2.57), (2.58), которые вычисляются по формулам:
(Pir ) |
−1 |
|
r |
|
|
|
|
|
= ∑ω(k) fi |
(k) fi(k), |
|||||
|
|
|
|
k=1 |
|
|
(2.66) |
( |
Pir )−1 |
r |
|
|
|||
|
|
|
|||||
= ∑ω(k) fis(k) |
fit(k), (s,t =1,..,m; i =1,2). |
||||||
|
|
st |
|
k=1 |
|
|
|
|
|
|
|
|
|
|
|
Правая часть в уравнениях (2.65) – это аналог векторов Y1, Y2 в уравнени-
ях (2.57), (2.58), вычисленных с учетом весовых коэффициентов ω(k) . Матричные уравнения (2.66) можно решить, например, умножая на пред-
варительно найденную матрицу Pir , обратную к информационной матрице
(Pir )−1. Тогда решение уравнений (2.66) можно записать в виде:
|
|
82 |
|
|
|
r |
|
(k) yi(k), (i =1,2). |
|
θɶir = Pir ∑ω(k) |
fi |
(2.67) |
||
k=1
Вэтом случае мы имели бы дело с «непоследовательной» идентификацией, то есть случаем, когда сначала выполняется вся серия измерений, а затем по их результатам методом максимального правдоподобия находится оценка параметров модели. Такое решение уже было получено выше.
Приступая непосредственно к обсуждению алгоритма последовательной идентификации в рассматриваемой задаче, матричные уравнения (2.66) запишем следующим образом:
(Pir ) |
−1 |
|
r−1 |
|
(k) yi(k) + ω(r) |
|
(r) yi(r), |
(i =1,2). |
|
|
θɶir = ∑ω(k) |
fi |
fi |
(2.68) |
|||||
k=1
Для первого слагаемого в правой части этих уравнений имеют место равенства:
r−1 |
|
(k) yi(k) =(Pir−1 ) |
−1 |
|
(i =1,2). |
|
∑ω(k) |
fi |
|
θɶir−1, |
(2.69) |
k=1
Сучетом этого равенства из уравнений (2.68) следует:
(Pir ) |
−1 |
|
−1 |
|
+ ω(r) |
|
(r) yi(r), |
(i =1,2). |
|
|
θɶir = (Pir−1 ) |
|
θɶir−1 |
fi |
(2.70) |
Теперь эти уравнения представим в виде:
(Pir )−1 θɶir = (Pir−1 )−1 θɶir−1 + ω(r) fi(r) (yi(r) − (fi(r),θɶir−1 ))+
|
|
|
−1 |
|
+ ω(r) |
|
|
|
|
+ω(r) ( fi |
(r) fi |
(r) )θɶir−1 = (Pir ) |
|
θɶir−1 |
fi |
(r) (yi(r) − (fi |
(r),θɶir−1 )), |
(2.71) |
(i =1,2).
Всвою очередь, из этих уравнений следует:
|
+ Pirω(r) |
|
|
|
|
θɶir = θɶir−1 |
fi |
(r) (yi(r) − (fi |
(r),θɶir−1 )), (i =1,2). |
(2.72) |
Это достаточно важный результат: соотношения (2.72) представляют собой рекуррентные формулы для оценивания коэффициентов модели θɶir .
Для расчета коэффициентов модели по формулам (2.72) необходимо получить и рекуррентные формулы вычисления матриц (Pir ). Как и ранее, с этой целью воспользуемся леммой об обращении матриц [2]. Формулу (2.66) для матрицы (Pir ) представим в виде:

83
(Pir )−1 (Pir )−1
r |
|
|
|
r−1 |
|
|
|
|
|
|
|
= ∑ω(k) |
fi |
(k) fi |
(k) |
= ∑ω(k) |
fi |
(k) fi |
(k) |
+ ω(r) |
fi |
(r) fi |
(r) |
k=1 |
|
|
|
k=1 |
|
|
|
|
|
|
(2.73) |
=(Pir−1 )−1 + ω(r) fi(r) fi(r) , (i =1,2).
Последнее слагаемое в этой формуле представим в виде:
ω(r) fi(r) fi(r) = Hi(r) Hi(r) = 
 ω(r) fi(r)
ω(r) fi(r) 
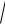 ω(r) fi(r),Hi(r) =
ω(r) fi(r),Hi(r) = 
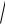 ω(r) fi(r) . (2.74)
ω(r) fi(r) . (2.74)
Тогда выражение (2.73) можно записать в виде:
(Pir ) |
−1 |
= (Pir−1 ) |
−1 |
|
|
|
|
+ Hi(r) Hi(r) . |
|||
Умножая обе части этого равенства слева на матрицу дующий результат:
(2.75)
Pir , получим сле-
|
E = Pir (Pir−1 ) |
−1 |
+ Pir |
|
|
|
|
|
|
||||||
|
|
|
Hi(r) Hi(r) , |
|
|
(2.76) |
|||||||||
где E – единичная матрица. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Это последнее равенство умножим на матрицу |
Pr−1 |
справа. В итоге полу- |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
чим выражение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pr−1 |
= Pr + Pr H |
(r) |
H(r)Pr−1 . |
|
|
(2.77) |
||||||||
|
i |
i |
i |
|
|
i |
|
|
i |
i |
|
|
|
|
|
Умножим теперь это выражение справа на вектор H(r) . В итоге получим: |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pr−1H |
(r) = Pr H |
(r) + Pr H |
(r) H |
(r)Pr−1H(r) = |
|
|
|||||||||
i |
i |
i |
i |
|
i |
|
|
i |
|
i i |
i |
|
|
(2.78) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= Pir Hi(r) (1+ Hi(r)Pir−1Hi(r) ). |
|
|
|
|
|
||||||||||
Наконец, это последнее выражение умножим на величину |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
||
|
(1+ Hi(r)Pir−1Hi(r) ) |
|
Hi(r)Pir−1 . |
|
|
|
(2.79) |
||||||||
В результате получаем следующее выражение: |
|
|
|
|
|||||||||||
|
|
|
|
) |
−1 |
|
|
|
|
|
|
|
|
|
|
Pir−1Hi(r) (1+ Hi(r)Pir−1Hi(r) |
|
Hi(r)Pir−1 = Pir |
Hi(r) |
Hi(r)Pir−1 . |
(2.80) |
||||||||||
Подстановка в эту формулу выражения (2.77) для Pr H(r) H |
(r)Pr−1 |
дает: |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
i |
i |
i i |
|
|
|
|
|
|
|
) |
−1 |
|
|
|
|
|
|
||
Pir−1Hi(r) (1+ Hi(r)Pir−1Hi(r) |
|
|
Hi(r)Pir−1 = Pir−1 − Pir . |
|
(2.81) |
||||||||||
Таким образом, из выражения (2.81) вытекает следующая рекуррентная формула для вычисления матриц Pir :
|
|
|
|
−1 |
|
Pir = Pir−1 |
− Pir−1Hi(r) (1 |
+ Hi(r)Pir−1Hi(r) ) |
Hi(r)Pir−1 . |
(2.82) |
|

84
Достаточно важно то, что при вычислении матриц Pir по этой формуле не требуется выполнение процедуры обращения матриц, так как величина (1+ Hi(r)Pir−1Hi(r) )−1 – скаляр.
Для начала процедуры последовательной идентификации по рассмотренным формулам необходимо каким-то образом определить матрицы Pi0 и
начальные оценки коэффициентов модели θɶi0 . Рекомендуется в качестве |
|||||||||||||||
начальных приближений задавать матрицы P0 в виде: |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
P0 |
= |
1 |
E, |
ε =10−3 ÷10−8 |
(i =1,2). |
(2.83) |
||||||
|
|
|
|
||||||||||||
|
|
|
|
i |
|
|
ε |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
В качестве начальной оценки параметров модели θɶi0 |
за неимением лучше- |
||||||||||||||
го выбирают оценку: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
θɶ0 |
= 0, (i =1,2). |
|
|
|
|
(2.84) |
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
Тогда для вычисления коэффициентов модели θɶir на очередной итерации |
|||||||||||||||
с номером r и матриц Pr |
имеют место рекуррентные формулы: |
||||||||||||||
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
θɶi0 = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
P0 |
= |
1 |
E,ε =10−3 ÷10−8, |
|
|
|
|
|
|||||||
|
|
|
|
|
|
||||||||||
i |
|
ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.85) |
||
|
|
|
|
|
|
|
|
|
|
|
|||||
H(r) = |
|
ω(r) f |
(r), |
|
|
|
|
|
|||||||
i |
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
−1 |
|
|
|
Pir = Pir−1 − Pir−1Hi(r) |
(1+ Hi(r)Pir−1Hi(r) |
|
Hi(r)Pir−1, |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
θɶir |
= θɶir |
−1 + Pirω(r) fi(r) (yi(r) − (fi(r) |
,θɶir−1 )), |
(i |
=1,2). |
||||||||||
Процедура вывода этих расчетных формул гарантирует, что получаемая таким образом последовательная оценка коэффициентов модели θɶir по точности практически полностью (за исключением возможных различий, обусловленных округлением результатов промежуточных вычислений) соответствует оценке по методу максимального правдоподобия, но не требует применения алгоритма обращения матриц.

85
··························· 


 Пример ························
Пример ························
В рассматриваемом примере (см. пп. 2.3.2, 2.3.3) для вычислений по формулам (2.85) необходимо задать начальное приближение и весовые коэффициенты, например:
θɶ0 = (0.0 0.0 0.0), |
(i =1), θɶ0 |
= (0.0 |
0.0 |
0.0), (i = 2), |
||||||||
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
ε = 0.1000E–04, |
ω(k) |
=1, k =1,2,..., N = 30, |
|
|
||||||||
|
1 |
|
0.1000E+01 |
0.0000E+00 |
0.0000E+00 |
|
||||||
P0 = |
|
0.0000E+00 |
0.1000E+01 |
0.0000E+00 |
. |
|||||||
|
– |
|
||||||||||
i |
|
|
|
|
|
|
|
|
|
|
||
|
0.1000E 04 |
|
|
|
|
|
|
|
|
|
||
|
|
0.0000E+00 |
0.0000E+00 |
0.1000E+01 |
||||||||
|
|
|
|
|
||||||||
Для первого приближения, сохраняя четыре знака после запятой, получа- |
||||||||||||
ем следующий результат: |
|
|
|
|
|
|
|
|
|
|
||
Aɶ |
= −0.4950E+01, Aɶ |
|
=0.0000E+00, Bɶ |
= 0.5050E+01, |
|
|||||||
11 |
|
|
|
|
12 |
|
|
11 |
|
|
|
|
Aɶ |
=0.5525E+00, Aɶ |
|
= −0.1000E+02, |
Bɶ |
= 0.5525E+00, (r =1). |
|||||||
21 |
|
|
|
22 |
|
|
|
22 |
|
|
|
|
Здесь необходимо напомнить о том, что при идентификации параметров говорить о точности идентификации можно только тогда, когда количество измерений превышает количество идентифицируемых параметров (в нашем случае три для каждого из уравнений (2.57), (2.58)). Поэтому первые могут давать результат, очень далекий от правильной оценки.
Четвертая итерация (количество измерений превысило количество идентифицируемых параметров) дает следующую оценку:
Aɶ |
= −0.1326E+01, Aɶ |
|
=0.7592E+00, Bɶ |
|
= 0.1425E+01, |
|
||
11 |
|
12 |
|
11 |
|
|
||
Aɶ |
=0.1254E+00, Aɶ |
|
= 0.9717E+00, |
Bɶ |
|
= 0.1229E+01, |
(r = 4). |
|
21 |
22 |
|
|
22 |
|
|
||
На пятнадцатом шаге получаем: |
|
|
|
|
||||
Aɶ |
= −0.9489E+00, Aɶ |
|
=0.1001E+01, Bɶ |
|
= 0.1052E+01, |
|
||
11 |
|
12 |
|
11 |
|
|
||
Aɶ |
=0.6397E–02, v |
= 0.1052E+01, Bɶ |
= 0.1100E+01, (r =15). |
|||||
21 |
22 |
|
|
|
22 |
|
|
|
Тридцатая итерация приводит к следующим уточненным оценкам, полученным методом последовательной идентификации (иногда говорят: методом последовательной регрессии):
Aɶ11 = −0.9491E+00, Aɶ12 =0.1001E+01, Bɶ11 = 0.1052E+01,
Aɶ21 =− 0.5944E–02, Aɶ22 = 0.1054E+01, Bɶ22 = 0.1109E+01, (r = 30).

86
Напомним, что метод максимального правдоподобия (непоследовательная идентификация) в данном случае привел к следующей оценке:
Aɶ11 = −0.9491E+00, Aɶ12 =0.1001E+01, Bɶ11 = 0.1052E+01,
Aɶ21 = −0.5978E–02, Aɶ22 = 0.1054E+01, Bɶ22 = 0.1109E+01.
Сравнивая результаты, можно заметить, что два этих метода дают близкие по точности оценки коэффициентов, что и следовало ожидать в соответствии с теорией.
Таким образом, по результатам идентификации в соответствии с нашей гипотезой (2.48) мы можем записать полученные уравнения модели:
dx1 (t)dtdx2 (t)
dt
= −0.95x1 (t)+1.00x2 (t)+1.05u1 (t),
(2.86)
= −0.01x1 (t)+1.05x2 (t)+1.11u2 (t), t [0,3].
·······································································

 ·····························································
·····························································
 Контрольные вопросы по главе 2
Контрольные вопросы по главе 2
·····························································
1.Запишите в общем виде уравнение состояния линейной стационарной динамической системы.
2.Запишите уравнение выходов линейной стационарной динамической системы.
3.Дайте определение линейного преобразования динамической системы.
4.Какие ограничения накладываются на выбор матрицы линейного преобразования?
5.Запишите уравнение, решение которого дает собственные числа для линейной стационарной динамической системы.
6.Докажите, что линейное преобразование не изменяет собственных чисел линейной системы управления.
7.Дайте определение канонического преобразования линейной системы.
8.Опишите алгоритм прямого определения собственных векторов.
9.Опишите процедуру определения собственных векторов на основе метода Крылова.
87
10.К каким наиболее существенным изменениям приводит процедура диагонализации линейной системы?
11.Дайте определение управляемой системы.
12.Сформулируйте критерий управляемости Гильберта.
13.Сформулируйте критерий управляемости на основе разложения матричной экспоненты.
14.Дайте определение управляемости по выходу.
15.Сформулируйте критерий управляемости по выходу.
16.Дайте определение наблюдаемой системы.
17.Сформулируйте критерий наблюдаемости Гильберта.
18.Сформулируйте критерий наблюдаемости на основе разложения матричной экспоненты.
19.Как осуществляется переход от непрерывной модели линейной стационарной динамической системы к дискретной модели?
20.Запишите в общем виде уравнения дискретной модели для системы с двумя переменными состояния, одним входным сигналом и двумя выходами.
21.Укажите рекомендуемый диапазон задания параметра ε в процедуре последовательной идентификации.

88
3 Идентификация параметров нелинейных стационарных динамических систем методом квазилинеаризации
Метод квазилинеаризации [2, 10, 11] предложили Р. Беллман и Р. Калаба. Этот метод основан на сведении нелинейной краевой задачи к линейной нестационарной задаче. При этом предполагается, что идентифицируемые параметры постоянны, по крайней мере на интервале моделирования системы. Кроме того, тип нелинейности, т. е. вид нелинейных уравнений идентифицируемой системы, также предполагается известным априорно. Если идентифицируемые параметры меняются относительно медленно по сравнению со скоростью сходимости алгоритма идентификации, то такая нестационарность параметров системы также может быть учтена. Как и для большинства методов линеаризации, не только скорость сходимости решения, но и успех решения задачи вообще существенно зависит от выбора начального приближения для идентифицируемых параметров. Метод квазилинеаризации применим как для идентификации параметров систем при известных начальных данных, так и для идентификации параметров (коэффициентов в уравнениях состояния) и начальных данных.
3.1 Постановка задачи идентификации параметров нелинейных стационарных динамических систем методом квазилинеаризации при известных начальных данных

 ·····························································
·····························································
 Рассмотрим систему, закон функционирования которой описывается системой обыкновенных нелинейных дифференциальных
Рассмотрим систему, закон функционирования которой описывается системой обыкновенных нелинейных дифференциальных
уравнений вида: |
|
|
|
||
|
dx(t) |
= f (t,x(t),u(t),θ), t t |
(0),T |
, |
|
|
|
||||
|
dt |
|
|
(3.1) |
|
|
x(t(0) )= x(0), |
|
|
|
|
где t t(0),T – контролируемая независимая переменная (напри- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
мер, |
время); |
|
|
t(0),T |
– |
интервал |
моделирования; |
||||
|
|
|
|
|
|
|
|
|
|
|
|
x = x(t) |
={x |
(t),x |
(t),...,x (t)} |
– |
вектор переменных |
|
состояния; |
||||
|
1 |
|
2 |
|
|
n |
|
|
|
|
|
u(t) ={u (t),...,u |
(t)} |
– |
вектор |
управления; θ ={θ ,...,θ |
m |
} – вектор |
|||||
|
1 |
l |
|
|
|
|
|
|
1 |
|
|
параметров;
89
f (t,x(t),u(t),θ) = { f1 (t,x(t),u(t),θ),..., fn (t,x(t),u(t),θ)} – известного вида векторная функция всех своих аргументов, в общем случае нелинейная; x(t(0) )= x(0) – заданный вектор, который определя-
ет начальное состояние системы.
·····························································
Как и ранее, нижние индексы будем использовать для обозначения номеров компонент векторов или элементов матриц, а верхний индекс, взятый в скобки, – для указания точки на оси времени и номера измерения.
В общем случае система уравнений (3.1) представляет собой систему нелинейных уравнений относительно неизвестных переменных состояния x(t) с
неизвестными параметрами θ, однако предполагается, что уравнения записаны
в форме, разрешенной относительно производной |
dx(t) |
. |
||||
dt |
||||||
|
|
|
|
|
||
Уравнение выходов моделируемой системы представлено системой ли- |
||||||
нейных алгебраических уравнений вида |
|
|
||||
|
|
|
y(t) = Сx(t), |
|
(3.2) |
|
где y(t) = {y |
(t),..., y |
k |
(t)} – вектор измеряемого |
выходного сигнала; |
||
1 |
|
|
|
|
||
C11 ...
C = ... ...
Ck1 ...
C1n
... – заданная прямоугольная матрица коэффициентов.
Ckn
Далее будем исходить из того, что результатом наблюдений за функцио-
нированием системы |
являются |
измерения |
значений выходного сигнала |
|
y(t( j) )= y( j) |
и вектора управления |
u(t( j) )= u( j) , выполненных в равноотстоя- |
||
щих узлах |
t( j) = t(0) + ∆t( j −1), ( j =1,2,..., N ) |
на оси времени. Тогда для пере- |
||
менных состояния x(t) |
моделируемой системы в соответствии с алгебраиче- |
|||
ским уравнением выходов (3.2) можно записать следующую систему алгебраических уравнений:
Сx( j) = y( j), t( j) = t(0) + ∆t( j −1), ( j =1,2,...,N ), |
(3.3) |
где y( j), ( j =1,2,...,N ) – измеренное значение выходного сигнала в общей серии длиной N измерений, а верхний индекс, который указывает на номер момента

90
времени измерений, взят в скобки, чтобы отличать его от номера компонент вектора, а затем и от номера итерации.
Для упрощения здесь принято, что измерения выполняются в равноотсто-
|
|
( |
) |
|
( |
) |
(0) |
|
ящих узлах |
t |
j |
|
= t |
0 |
|
+ ∆t( j −1) t |
,T , ( j =1,2,...,N ) на оси времени, и при |
|
|
|
|
этом шаг ∆t достаточно мал. Выполнение этого условия не обязательно, но если оно не выполняется, то в последующем может потребоваться дополнительная процедура совмещения узлов, в которых выполняются измерения выходного сигнала и методом квазилинеаризации находятся значения переменных состояния.
·····························································

 Изучаемую систему будем считать стационарной, по крайней
Изучаемую систему будем считать стационарной, по крайней  мере в течение времени, необходимого для идентификации параметров. На этом основании для идентифицируемых параметров можно записать следующую систему обыкновенных дифференци-
мере в течение времени, необходимого для идентификации параметров. На этом основании для идентифицируемых параметров можно записать следующую систему обыкновенных дифференци-
альных уравнений: |
|
||
|
dθ |
= 0. |
(3.4) |
|
|
||
|
dt |
|
|
·····························································
Решение уравнений (3.1) должно удовлетворять заданным, известным, начальным условиям вида:
x(t(0) )= x(0) . |
(3.5) |
Задача идентификации параметров моделируемой системы заключается в том, чтобы найти векторы переменных состояния x(t) и коэффициентов моде-
ли θ, которые удовлетворяют системам дифференциальных уравнений (3.1), (3.4), начальным условиям (3.5), а также уравнению выходов (3.3). При этом предполагается, что при известных значениях параметров θ начальных условиях (3.5) решение системы (3.1) единственно. Следует ещё раз подчеркнуть, в рассматриваемом случае начальное состояние системы считается известным, что несколько упрощает задачу.
·····························································
 Приведенные уравнения представляют собой математическое
Приведенные уравнения представляют собой математическое  выражение априорно принятой гипотезы о внутреннем устройстве реальной системы, которая является результатом первого этапа идентификации. На этом этапе установлено, что входное воздей-
выражение априорно принятой гипотезы о внутреннем устройстве реальной системы, которая является результатом первого этапа идентификации. На этом этапе установлено, что входное воздей-
