
6552
.pdf
31
и по таблицам определяют значение критерия Кочрена для степеней свободы fi max = r −1, fi = N для уровня значимости α = 5%. Если Gtabl > G , то гипотеза об однородности дисперсий принимается.
4.На следующем, очень важном шаге, по T-критерию Стьюдента проверяется значимость коэффициентов модели. Для этого находится дисперсия коэффициентов регрессии:
S2 (θ j )= |
1 |
S2 (y) – |
(1.59) |
|
|||
|
Nr |
|
|
и по таблицам распределения случайных величин определяют критическое значение Tcr критерия Стьюдента для степеней свободы f = N (r −1) и уровня значимости α = 5%. По этому значению строит-
ся интервал длиной r∆θ j , ∆θ j = Tcr S (θ j ), где ∆θ j – половина длины доверительного интервала. Если абсолютная величина коэффициента θ j > ∆θ j , то коэффициент считается значащим (им нельзя прене-
бречь), в противном случае соответствующий коэффициент считается незначащим и далее в модели не учитывается.
Это очень важный шаг, т. к. если все коэффициенты модели оказываются значащими, то это означает, что количество опытов равно количеству значащих коэффициентов модели. Отсюда следует, что модель должна быть признана неадекватной, т. к. в соответствии с формулой для оценки дисперсии на основании теоремы Гаусса – Маркова дисперсия будет бесконечно велика, что проявляется на следующем шаге.
5.Формальная проверка адекватности модели выполняется на основе критерия Фишера. С этой целью вычисляют дисперсию адекватности:
|
|
N |
|
|
|
|
Sad2 = |
r |
∑(y |
(i) − yɶ |
(i) )2 , |
(1.60) |
|
N − mɶ |
||||||
|
i=1 |
|
|
|
||
где mɶ – количество значащих коэффициентов модели, а |
yɶ(i) – значе- |
|||||
ние выходного сигнала, вычисленное по принятому уравнению (1.51) модели после отбрасывания (приравнивания к нулю) незначащих коэффициентов. После этого вычисляют значение критерия Фишера: F =Sad2 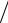 S2 (y). Из таблиц находят критическое значение критерия Фишера Fcr для степеней свободы Fad = N − mɶ и fk = N (r −1) и за-
S2 (y). Из таблиц находят критическое значение критерия Фишера Fcr для степеней свободы Fad = N − mɶ и fk = N (r −1) и за-

32
данного уровня значимости α. При выполнении условия F < Fcr модель признается адекватной.
6. Вычисляют коэффициент множественной корреляции:
R = 1− |
N=8 |
|
|
|
|
N=8 |
|
|
|
, |
|
∑(y |
(i) − yɶ |
(i) )2 |
∑(y |
(i) − |
|
)2 |
(1.61) |
||||
y |
|||||||||||
|
i=1 |
|
|
|
|
i=1 |
|
|
|
|
|
где y – среднее значение y(i) . Значение этого коэффициента находится в пределах 0 ≤ R ≤1. Если значения R близки к нулю, то коэффициенты модели не вносят вклада в изучаемую зависимость. Если же он близок к единице, то принятое уравнение полностью описывает результаты эксперимента.
·························· 


 Пример ························
Пример ························
Пусть требуется найти параметры модели:
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y(u1,u2 ,u3 ) |
= ∑ f j (u)θ j , |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
j=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
(u) =1, f |
2 |
(u) = u , f |
3 |
(u) |
= u |
2 |
, f |
4 |
(u) = u , |
|
|
||||||||
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
3 |
|
|
||||||
f |
5 |
(u) = u u |
2 |
, f |
6 |
(u) = u |
|
u , f |
7 |
(u) = u u , f |
8 |
(u) = u u u , |
|||||||||
|
1 |
|
|
2 |
|
3 |
|
|
|
|
3 |
1 |
1 |
2 |
3 |
||||||
для которой матрица плана и результаты измерений выходного сигнала приведены в таблице 1.2.
Таблица 1.2 – Факторный план типа 23
Матрица планирования 23
№ опыта |
|
|
Базисные функции |
|
|
Выходной сигнал |
|||||||
f1 |
f2 |
|
f3 |
f4 |
f5 |
f6 |
|
f7 |
f8 |
y(i),1 |
y(i),2 |
y(i) |
|
|
|
|
|||||||||||
1 |
+ |
+ |
|
+ |
+ |
+ |
+ |
|
+ |
+ |
–11.5 |
–10.5 |
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
+ |
– |
|
+ |
+ |
– |
+ |
|
– |
– |
–12.5 |
–11.5 |
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
+ |
+ |
|
– |
+ |
– |
– |
|
+ |
– |
–20.5 |
–23.5 |
22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
+ |
– |
|
– |
+ |
+ |
– |
|
– |
+ |
–21.5 |
–22.5 |
22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
+ |
+ |
|
+ |
– |
+ |
– |
|
– |
– |
–24.5 |
–21.5 |
23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
+ |
– |
|
+ |
– |
– |
– |
|
+ |
+ |
–25.5 |
–24.5 |
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
+ |
+ |
|
– |
– |
– |
+ |
|
– |
+ |
–28.5 |
–27.5 |
28 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
+ |
– |
|
– |
– |
+ |
+ |
|
+ |
– |
–33.5 |
–30.5 |
32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|

33
1 r=2
Находим среднее значение y(i) = 2 ∑p=1 y(i), p выходного сигнала для каждой
экспериментальной точки по всем повторным измерениям и заносим эти значения в последний столбец таблицы 1.2.
Находим оценки параметров:
|
|
N=8 |
|
θ j = ∑ f j (u(i) )y(i) 8 |
|
||
|
|
i=1 |
|
θɶ |
|
= (11+12 + 22 + 22 + 23+ 25 + 28 + 32) 8 = 21.875, |
|
1 |
|
|
|
θɶ |
2 |
= (11−12 + 22 − 22 + 23− 25 + 28 − 32) |
8 = −0.875, |
θɶ |
3 |
= (11+12 − 22 − 22 + 23+ 25 − 28 − 32) |
8 = −4.125, |
θɶ |
4 |
= (11+12 + 22 + 22 − 23− 25 − 28 − 32) |
8 = −5.125, |
θɶ |
5 |
= (11−12 − 22 + 22 + 23− 25 − 28 + 32) |
8 = 0.125, |
θɶ |
6 |
= (11+12 − 22 − 22 − 23− 25 + 28 + 32) |
8 = −1.125, |
θɶ |
7 |
= (11−12 + 22 − 22 − 23+ 25 − 28 + 32) |
8 = 0.625, |
θɶ |
8 |
= (11−12 − 22 + 22 − 23+ 25 + 28 − 32) |
8 = −0.375. |
Находим построчные дисперсии и дисперсию воспроизводимости:
|
1 |
r |
|
|
|
|
|
|
|
(σ(i) )2 = |
∑(y |
(i), p |
− y(i) )2 (σ(1) )2 = 0.5, (σ(2) )2 |
= 0.5, (σ(3) )2 = 4.5, |
|||||
|
|
|
|
||||||
|
r −1 p=1 |
|
|
|
|
|
|
||
(σ(4) )2 = 0.5, (σ(5) )2 = 4.5, (σ(6) )2 = 0.5, (σ(7) )2 = 0.5, (σ(8) )2 = 4.5, |
|||||||||
S2 (y) = |
1 ∑(σ(i) )2 |
= |
|
1 ∑∑(y(i), p − y(i) )2 = |
2. |
||||
|
|
N |
|
|
|
|
N r |
|
|
|
N i=1 |
|
|
|
N(r −1) i=1 p=1 |
|
|||
Проверяем однородность дисперсий по критерию Кочрена. Расчет отношения максимальной построчной дисперсии к дисперсии воспроизводимости дает:
|
|
(i) |
) |
2 |
|
|
|
|
|
max(σ |
|
|
|
4.5 |
|
|
|
G = |
|
|
|
|
= |
0.2813. |
|
|
∑(σ(i) )2 |
|
16 |
|
|||||
|
N |
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
Для степеней свободы fi max = r −1=1, fi = N = 8 критическое |
значение |
|||||||
критерия Кочрена Gtabl = 0.6798 при уровне значимости α = 5%, Gtabl |
> G , дис- |
|||||||
персии однородны. |
|
|
|
|
|
|
|
|
Находим полуширину доверительного интервала: |
|
|||||||

34
S2 (θ j )= Nr1 S2 (y) =1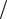 8, Tcr = 2.306, ∆θ j = Tcr S (θ j )= 0.815.
8, Tcr = 2.306, ∆θ j = Tcr S (θ j )= 0.815.
Проверка значимости коэффициентов по условию θ j > ∆θ j дает, что значащими являются 5 коэффициентов:
θɶ1 = 21.875, θɶ2 = −0.875, θɶ3 = −4.125,θɶ4 = −5.125, θɶ6 = −1.125.
Итак, уравнение модели с учетом только значащих коэффициентов имеет
вид:
y = 21.875 f1 (u)− 0.875 f2 (u)− 4.125 f3 (u)− 5.125 f4 (u)−1.125 f6 (u).
По этому уравнению находим расчетные значения выходного сигнала в точках плана:
y = 21.875 f1 (u)− 0.875 f2 (u)− 4.125 f3 (u)− 5.125 f4 (u)−1.125 f6 (u)
yɶ(1) yɶ(2) yɶ(3) yɶ(4) yɶ(5) yɶ(6)
=21.875 − 0.875 − 4.125 − 5.125 −1.125 =10.625,
=21.875 + 0.875 − 4.125 − 5.125 −1.125 =12.375,
=21.875 − 0.875 + 4.125 − 5.125 +1.125 = 21.125,
=21.875 + 0.875 + 4.125 − 5.125 +1.125 = 22.875,
=21.875 − 0.875 − 4.125 + 5.125 +1.125 = 23.125,
=21.875 + 0.875 − 4.125 + 5.125 +1.125 = 24.875,
yɶ(7) = 21.875 − 0.875 + 4.125 + 5.125 −1.125 = 29.125, yɶ(8) = 21.875 + 0.875 + 4.125 + 5.125 −1.125 = 30.875. Находим дисперсию адекватности:
|
|
N |
|
|
|
Sad2 = |
r |
∑(y |
(i) − yɶ |
(i) )2 = |
|
N − mɶ |
|||||
|
i=1 |
|
|
= 8 −2 5((0.375)2 + (0.375)2 + (0.875)2 + (0.875)2 + (0.125)2 )+ + ((0.125)2 + (1.125)2 + (1.125)2 )= 2.92.
Проверяем выполнение критерия Фишера:
F = S |
S2 |
2.92 |
=1.46. |
|
2 (y)= |
2 |
|||
|
|
ad |
|
|
Так как Fcr =4.07>F =1.46, то модель признается адекватной. Необходимо отметить, что это формальная проверка адекватности, кото-
рая мало что дает в плане оценки правильности понимания физической сущности моделируемых процессов. Кроме того, область применимости полученной
35
модели ограничена интервалом изменения входных переменных ui [−1:1], возможность выхода за границы которого требует дополнительных исследований.
Коэффициент множественной корреляции в рассматриваемом примере равен:
|
N=8 |
|
|
|
|
|
|
|
|
|
|
|
|
∑(y |
(i) − yɶ |
(i) )2 |
|
|
|
|
|
||||
R = 1− |
= 1− |
4.375 |
= 0.99 , |
|||||||||
i=1 |
|
|
|
|
|
|||||||
N=8 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
∑(y |
(i) − |
|
)2 |
366.875 |
|
|
|||||
|
y |
|||||||||||
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
следовательно, модель хорошо описывает экспериментальные данные.
·······································································
1.7 Метод последовательной идентификации
Рассмотрим метод последовательной идентификации линейных стационарных систем, который по точности дает такие же результаты, как и метод максимального правдоподобия, но требует меньших объемов компьютерной памяти и времени счета. Алгоритм последовательной идентификации частично снимает вычислительные проблемы, связанные с явным или неявным обращением информационной матрицы. Метод применим к процессам, которые можно считать стационарными не менее чем на m интервалах времени, в течение которых осуществляется идентификация m неизвестных параметров системы.
1.7.1 Последовательная идентификация одномерной системы
Одномерной системой называется система с одним входом и одним выходом. Рассмотрим простейшую скалярную линейную статическую одномерную систему (т. е. систему, для которой коэффициенты модели и состояние явно от времени не зависят), которая описывается уравнением:
y = uθ . (1.62) В соответствии с принятым уравнением модели для каждой экспериментальной точки при выполнении серии измерений входного и выходного сигна-
лов имеют место уравнения:
y(i) = y0(i) + µ(i) = u(i)θ, (i =1,2,...,N ), |
(1.63) |
где y(i) – измеряемый выходной сигнал, y0(i) – предполагаемое точное значение выходного сигнала, µ(i) – случайная ошибка измерений, i =1,2,...,N – номер опыта.

36
Прежде всего, задача оценки неизвестного параметра θ системы может быть решена уже известным нам методом. Для этого запишем расчетные формулы, используя идеи метода наименьших квадратов.
Рассмотрим задачу минимизации среднеквадратического отклонения экспериментальных результатов y(i) и их расчетных значений y(i) = u(i)θɶN , которые
можно будет получить, если найти оценку параметра θɶN по результатам N измерений:
N |
|
JN = ∑ω(i) (y(i) − u(i)θɶN )2 . |
(1.64) |
i=1 |
|
Здесь, как и ранее, верхний индекс, взятый в скобки, – номер измерения, |
|
θɶN – оценка параметра θ, полученная в результате серии из N |
измерений, |
ω(i) – весовой коэффициент, который может быть принят равным единице, а может быть использован для того, чтобы повысить или понизить влияние отдельных измерений на оценку θɶN .
Из условия минимума функционала величины JN следует, что наилучшая оценка должна удовлетворять уравнению:
|
dJ |
N |
i |
|
i |
|
i |
|
i |
|
|
|
|
|
|
|
|
|
|||||
|
N |
= −2∑ω( |
)u |
( |
) (y( |
) − u |
( |
)θɶN )= 0. |
(1.65) |
||
|
ɶN |
|
|
||||||||
|
dθ |
i=1 |
|
|
|
|
|
|
|
|
|
Отсюда получаем оценку параметра θɶN : |
|
|
|
||||||||
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
θɶN = |
∑ω(i)u(i) y(i) |
|
|
|
|||||
|
|
i=1 |
|
|
|
|
. |
|
(1.66) |
||
|
|
N |
|
|
(u(i) )2 |
|
|||||
|
|
|
∑ω(i) |
|
|
|
|||||
i=1
Теперь получим оценку θɶN коэффициента θ методом последовательной идентификации. При этом результат такой последовательной оценки величины θ после N измерений будет совпадать с оценкой (1.66). Рассмотрим соответствующий процесс последовательного уточнения такой оценки. Первое измерение дает в соответствии с формулой (1.66) оценку
θɶ1 = |
ω(1)u(1) y(1) |
|
ω(1) (u(1) )2 . |
(1.67) |
Серия из двух измерений дает следующую уточненную оценку по формуле (1.66):

37
θɶ2 |
= |
ω(1)u(1) y(1) + ω(2)u(2) y(2) |
|
ω(1) (u(1) )2 + ω(2) (u(2) )2 . |
(1.68) |
Однако эту формулу можно привести к виду:
θɶ2 = θɶ1 − θɶ1 |
ω(1) (u(1) )2 + ω(2) (u(2) )2 |
|
|
|
ω(1)u(1) y(1) + ω(2)u(2) y(2) |
|||||||||||||||||||||||||||||||||||
|
|
|
|
+ |
|
|
|
= |
||||||||||||||||||||||||||||||||
ω(1) (u(1) )2 + ω(2) (u(2) )2 |
ω(1) (u(1) )2 + ω(2) (u(2) )2 |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
ω(1)u(1) (y(1) − u(1)θɶ1 )+ ω(2)u(2) (y(2) − u(2)θɶ1 ) |
|
|
|
|
|
(1.69) |
|||||||||||||||||||||||||||||
= θɶ1 + |
. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
ω(1) (u(1) )2 + ω(2) (u(2) )2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɶ1 |
Подстановка во второе слагаемое в формуле (1.69) выражения (1.67) для θ |
||||||||||||||||||||||||||||||||||||||||
дает следующий результат: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
1 |
|
|
1 |
ω(1)u(1) y(1) |
|
|
|
|
2 |
) ( |
2 |
) |
(y |
2 |
) |
|
2 |
) 1 |
) |
|
|||||||
|
|
|
|
|
|
|
|
|
|
( ) |
|
( ) |
( ) |
− u |
( ) |
|
|
|
|
|
|
|
|
|
+ ω |
( |
|
( |
− u |
( |
|
|||||||||
|
|
|
|
|
|
|
|
|
ω |
|
u |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
θɶ |
|
|||||||
|
|
|
|
|
|
|
|
1 |
1 |
) |
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω( ) |
(u( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
θɶ |
|
= θɶ |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
ω(1) (u(1) )2 + ω(2) (u(2) )2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.70) |
||||||||||||||||||
θɶ2 = θɶ1 + |
ω(2)u(2) (y(2) − u(2)θɶ1 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
ω(1) (u(1) )2 + ω(2) (u(2) )2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Продолжение этого процесса приводит к тому, что после измерения с но- |
||||||||||||||||||||||||||||||||||||||||
мером r (1≤ r ≤ N ) |
уточненная оценка коэффициента θɶr |
может быть получена |
||||||||||||||||||||||||||||||||||||||
в результате следующего итерационного процесса: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
θɶr = θɶr−1 + Prω(r)u(r) (y(r) − u(r)θɶr−1 ), 1≤ r ≤ N, |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
θɶ0 = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
1 |
|
|
|
= ω(1) (u(1) )2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.71) |
|||||||
|
|
|
P1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
1 |
|
= ω(1) (u(1) )2 + ω(2) (u(2) )2 = |
1 |
+ ω(2) |
(u(2) )2 , |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
2 |
|
1 |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
1 |
|
|
|
|
r |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
= ∑ω(i) (u(i) |
)2 = |
|
+ ω(r) (u(r) )2 , r =1,2,...,N. |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
r |
r−1 |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
P |
|
i=1 |
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Процесс последовательного уточнения (1.71) дает такое же значение |
||||||||||||||||||||||||||||||||||||||||
оценки коэффициента модели θɶN |
по результатам |
N измерений, что и оценка |
||||||||||||||||||||||||||||||||||||||
(1.66) по методу наименьших квадратов, если не считать некоторой разницы в результате округления при компьютерных расчетах. С другой стороны, схема
38
(1.71) может быть признана предпочтительной, так как в этом случае расчеты ведутся по рекуррентным формулам и не требуется хранения всех предыдущих результатов измерений.
1.7.2Последовательная идентификация многомерной системы
Рассмотрим линейную многомерную статическую систему с вектором
входного сигнала u = {u ,...,u }, скалярным выходным сигналом |
y и принятым |
|||||||
|
|
1 |
l |
|
|
|
|
|
по результатам предварительного изучения уравнением модели вида |
|
|
||||||
|
|
|
|
|
m |
|
|
|
|
|
|
у = ( f |
(u),θ)= ∑ f j (u)θ j , |
|
|
(1.72) |
|
|
|
|
|
|
j=1 |
|
|
|
где θ = {θ ,...,θ |
m |
} – вектор оцениваемых параметров; f (u) = { f |
(u),..., f |
m |
(u)} – |
|||
1 |
|
|
|
1 |
|
|
||
вектор базисных функций модели (т. е. известного вида функций всех своих аргументов).
Результаты измерений входного и выходного сигналов в серии из (i =1,2,...,N ) измерений и уравнение (1.72) позволяют записать исходную си-
стему уравнений для оценки параметров: |
|
|
|
|
|
у(i) = y0(i) + µ(i) |
= f1 (u(i) )θ1 + f2 (u(i) )θ |
2 + ...+ fm (u |
|
|
|
(i) )θm = (f |
(u(i) ),θ). (1.73) |
||||
Как и ранее, здесь y |
(i) – предполагаемое точное значение выходного сигнала, |
||||
|
0 |
|
|
|
|
µ(i) – случайная ошибка (шум) измерений, i =1,2,...,N – номер опыта. |
|||||
Вновь воспользуемся идеями метода наименьших квадратов. Рассмотрим |
|||||
задачу минимизации среднеквадратического отклонения: |
|
||||
|
N |
|
|
2 |
|
|
JN = ∑ω(i) (y(i) − ( |
f |
(u(i) ),θɶN )) |
. |
(1.74) |
|
i=1 |
|
|
|
|
Здесь вновь верхний индекс, взятый в скобки, – номер измерения, θɶN – оценка вектора коэффициентов модели θ, полученная в результате серии из N измерений, ω(i) – неотрицательные весовые коэффициенты, которые выбираются с целью повысить или понизить влияние отдельного опыта на итоговую оценку параметров либо просто принимаются равными единице.
Из условия минимума функционала JN |
следует, что оценка θɶN |
должна |
||||||||
удовлетворять следующей системе уравнений: |
|
( |
|
|
)) |
|
|
|||
∂θɶNj |
i=1 |
|
( |
|
|
|
|
|
||
∂JN |
N |
(u(i) ) y(i) |
|
|
|
|
|
|||
= 0, −2∑ω(i) |
f |
− |
|
f |
(u(i) ),θɶN |
|
= 0 . |
(1.75) |
||

39
·····························································
Символом здесь обозначена операция внешнего умноже-
ния векторов, которая при умножении вектора a = {a ,...,a |
} |
на век- |
|||
|
|
1 |
s |
|
|
тор b = {b1,...,bt} дает матрицу размера (s ×t): |
|
|
|
||
a b = C, C |
= a b |
, i =1,2,...,s; j =1,2,...,t , |
|
|
(1.76) |
ij |
i j |
|
|
|
|
а если один из сомножителей скаляр – то эта операция означает обычное умножение вектора на число.
·····························································
Уравнения (1.75) есть не что иное, как нормальная система уравнений, которую мы уже получали, рассматривая метод максимального правдоподобия, которое теперь запишем в виде:
(PN )−1 θɶN = ∑N ω(i) f (u(i) )y(i) . i=1
Здесь символом (PN )−1 обозначена информационная матрица:
M= (PN )−1 = ∑N ω(i) f (u(i) ) f (u(i) ).
i=1
Элементы, стоящие на пересечении строки k, (k =1,2,...,m) j, ( j =1,2,...,m) этой матрицы вычисляются по формуле:
(PN )−kj1 = ∑N ω(i) fk (u(i) ) f j (u(i) ). i=1
(1.77)
(1.78)
и столбца
(1.79)
Решение уравнения (1.77) дает следующую оценку параметров модели по методу наименьших квадратов:
|
N |
|
(u(i) )y(i) . |
|
θɶN = PN ∑ω(i) |
f |
(1.80) |
||
i=1
Здесь, очевидно, матрица PN есть матрица, обратная к информационной:
PN = M −1 .
Однако оценку параметров θɶN модели на основе уравнения (1.77) можно получить и последовательным методом, не прибегая к процедуре обращения информационной матрицы. С этой целью матричное уравнение (1.77) представим в виде:
(PN ) |
−1 |
|
N−1 |
|
(u(i) )y(i) + ω(N ) |
|
(u(N ) )y(N ) . |
|
|
θɶN = ∑ω(i) |
f |
f |
(1.81) |
||||
i=1

40
Для первого слагаемого в правой части этого уравнения имеет место равенство:
N−1 |
|
(u(i) )y(i) = (PN−1 ) |
−1 |
|
∑ω(i) |
f |
|
θɶN−1 . |
i=1
Поэтому уравнение (1.81) можно преобразовать к виду:
(PN )−1 θɶN = (PN−1 )−1 θɶN−1 + ω(N ) f (u(N ) )y(N ) .
Это уравнение в свою очередь представим в виде:
(PN )−1 θɶN = (PN−1 )−1 θɶN−1 + ω(N ) (f (u(N ) ) f (u(N ) ))θɶN−1 +
+ω(N ) f (u(N ) ) (y(N ) − (f (u(N ) ),θɶN−1 )).
(1.82)
(1.83)
(1.84)
Объединяя два первых слагаемых в правой части, получаем уравнение:
(PN ) |
−1 |
|
−1 |
|
|
|
(u(N ) ) (y(N ) − ( |
|
|
|
|
|
θɶN = (PN ) |
θɶN−1 + ω(N ) |
f |
f |
(u(N ) ),θɶN−1 )). |
(1.85) |
|||||
Из этого уравнения следует: |
|
|
|
|
|
|
|
|
|||
|
|
|
|
(u |
|
|
|
|
|
|
|
θɶN |
= θɶN−1 + (PN )ω(N ) |
f |
(N ) ) (y(N ) − (f |
(u(N ) ),θɶN−1 )). |
(1.86) |
||||||
Формула (1.86) представляет собой рекуррентную формулу вычисления коэффициентов модели θɶN , но для её применения необходимо получить и рекуррентные формулы вычисления матрицы PN , обратной к информационной матрице. Для получения этих формул воспользуемся леммой об обращении матриц [2]. С этой целью формулу (1.78), которая определяет информационную матрицу, представим в виде:
(PN )−1 = ∑N ω(i) f (u(i) ) f (u(i) )=
i=1
N−1 |
|
|
(u(i) )+ ω(N ) |
|
|
(u(N ) ) |
|
= ∑ω(i) |
f |
(u(i) ) f |
f |
(u(N ) ) f |
(1.87) |
i=1
(PN )−1 = (PN−1 )−1 + ω(N ) f (u(N ) ) f (u(N ) ).
Последнее слагаемое в этой формуле представим в виде:
|
|
|
|
|
|
|
|
|
|
|
(u(N ) ) |
|
|
(u(N ) ), |
ω(N ) |
|
|
(N ) = |
ω(N) |
ω(N ) |
|||||||||
f |
(u(N ) ) f |
(u(N ) )= H |
(N ) H |
f |
f |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.88) |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(H |
(N ) |
= |
ω(N ) |
f (u(N ) )). |
|
|
|
|
|
|
|
|
||
Теперь формулу для информационной матрицы можно записать в виде:
(PN ) |
−1 |
= (PN−1 ) |
−1 |
|
|
(N ) . |
(1.89) |
|
|
+ H |
(N ) H |
