2549

3. ЭКСПЕРИМЕНТАЛЬНО-ТЕОРЕТИЧЕСКИЕ ПРЕДПОСЫЛКИ К МОДЕЛЯМ РАСПРЕДЕЛЕНИЯ НАПРЯЖЕНИЙ В ДОРОЖНЫХ КОНСТРУКЦИЯХ

Известно, что такие физические явления, как тепло, свет, звук, механические силовые импульсы распространяются в средах чаще всего экспоненциально. Даже ударные (взрывные) волны распространяются в грунтах экспоненциально с конкретным затуханием, то есть рассеиванием.

Для применения в решении аналитической задачи о воздействии на упругое полупространство подвижной нагрузки необходимы закономерности распределения динамических напряжений и перемещений в нем. Проделаем это путем выбора из известных экспериментальных данных значения коэффициента затухания в предположении, что напряжения убывают с глубиной по закону

экспоненты.

Коэффициент затухания напряжений в среде и коэффициент затухания перемещений с глубиной z определен экспериментально и

Его значение по данным разных авторов приведено в табл. 3.1.

Таблица 3.1

Значение коэффициента γ0

23

Сравнение этих данных с аналитическими формулами А.Е.Н. Love, М.И. Якунина и А.В. Смирнова, приведенное в табл. 3.2, указывает на существенно большее совпадение экспериментов с формулой А.В. Смирнова (5 раз вместо 1) и достоверно утверждает, что напряжения и перемещения убывают в упругом полупространстве при кратковременном нагружении по закону экспоненты, что дает убедительное основание для применения этого закона в аналитических построениях.

Таблица 3.2

Сравнение аналитических и экспериментальных коэффициентов затухания напряжений сжатия

24

* Эксперименты А.М. Шак выполнены в РФ под руководством д-ра техн. наук, проф. Ю.М. Яковлева.

Таблица 3.3

Расчетные значения коэффициента затухания напряжений в материалах дорожных покрытий*

* Расчет коэффициента 0 произведен на основе работы Р.И. Бляхмана [21].

4.ФОРМИРОВАНИЕ ВОЛН

ВУПРУГОМ ПОЛУПРОСТРАНСТВЕ

При горизонтальном движении вертикальной силы по гладкой поверхности упругой среды в ней развивается динамический процесс, характеризуемый временем воздействия нагрузки, ее распределением

ввиде напряжений сжатия, их убыванием по глубине среды, возникновением упругих перемещений и их убыванием (затуханием) с течением времени. Такая схема быстрого горизонтального движения вертикальных нагрузок свойственна проезжей части автомагистралей, дорог и взлетно-посадочным полосам аэродромов.

Известны два метода науки для математического описания динамических процессов, развивающихся во времени. Один из них – дифференциальная механика, второй – дискретная. В дифференциальной механике состояние среды, на которую действует механическое возмущение, характеризуют системой дифференциальных уравнений Лагранжа (уравнениями движения). Их разрешение дает относительно точное описание поведения среды

вмомент возмущения и позднее. Привлечение сложных функций (Хевисайда, Ханкеля, Бесселя, эллиптических интегралов) для получения числового результата приводит в большинстве случаев к ограничению применения их в практике. Дискретная механика

25

основана на математической логике. Суть её состоит в разделении непрерывного времени на дискретные отрезки, математическом описании поведения объекта явными и общеизвестными функциями в пределах каждого отрезка. В пределах каждого отрезка времени применяются основные начала механики: законы равновесия, сохранения количества движения, массы, энергии и т.д.

Рассмотрим закономерности, определяющие колебания и скорости колебаний поверхности упругого полупространства, а также напряжения в нем, как наиболее простой модели дорожной конструкции. При этом будем считать действие кратковременной нагрузки переменным во времени по закону синусоиды, а полупространство характеризовать следующими параметрами: модулем упругости среды Е0, плотностью среды ρ0, кг/м3; скоростью

где p – колесная нагрузка, распределенная по площадке диаметром D;

Т0 – время приложения нагрузки, Т0 =D (здесь V – скорость движения

V

нагрузки; D – диаметр площади распределения нагрузки); t – текущее время.

Эта формула характеризует приложение нагрузки, движущейся на поверхности полупространства со скоростью V по направлению оси x. Перемещение нагрузки вдоль этой оси предполагается прямолинейным.

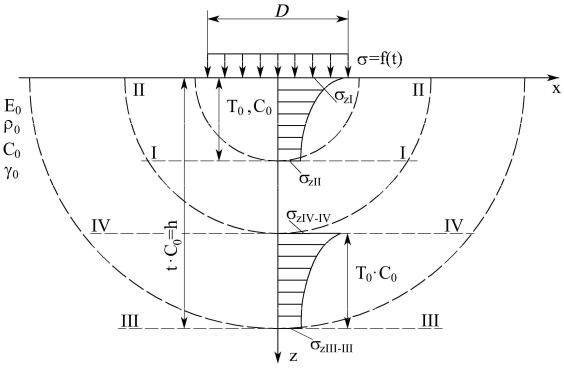
Рассмотрим процесс формирования фронта напряжений в упругом полупространстве по направлению оси z (x=0, y=0, t=0).

В период от 0 до tф формируется фронт напряжений сжатия, длина которого равна

В начале этого фронта напряжения в плоскости I-I (рис. 4.1) с учетом затухания равны

26

Рис. 4.1. Схема формирования сжимающих вертикальных напряжений в сплошном упругом полупространстве при действии кратковременной нагрузки, распределенной равномерно по кругу

Среднее напряжение до момента t = Т0 в пределах фронта волны сжатия определяется как

Вертикальные перемещения поверхности полупространства по оси z до времени t < T0 равны

27

При t>T0 фронт напряжений начинает отрываться верхней границей от поверхности полупространства и перемещаться вглубь по оси z. К моменту t>T0 напряжение в передней границе фронта в плоскости III-III будет равно

Скорость перемещений поверхности полупространства после t>T0 является первой производной по t предыдущего выражения (4.11), поэтому

28

5. ЧИСЛЕННЫЙ АНАЛИЗ ДИСКРЕТНОЙ МОДЕЛИ ВОЛНОВОГО ДИНАМИЧЕСКОГО ДЕФОРМИРОВАНИЯ УПРУГОГО ПОЛУПРОСТРАНСТВА

ПРИ ВОЗДЕЙСТВИИ ПОДВИЖНОЙ НАГРУЗКИ. АМПЛИТУДНО-ЧАСТОТНАЯ ХАРАКТЕРИСТИКА И ВИБРОКОЛЕБАНИЯ

Анализ проведен на основе расчетов по программе «Slag II», созданной в СибАДИ. Параметры динамического деформирования полупространства: динамический прогиб U , скорость прогиба U , ускорение прогиба U , частота колебаний , среднее напряжение сжатия и глубина их распространения в полупространстве z определены для полупространства с модулем упругости Е=100, 400, 1000 МПа, для плотности =2,5 г/см3 и параметра затухания

напряжений в нем 0 =0,01 см-1. Вертикальная нагрузка P=50 кН перемещалась горизонтально со скоростью 20÷180 км/ч. Из результатов расчетов следует, что:

1)динамические прогибы поверхности полупространства закономерно убывают с возрастанием скорости движения нагрузки в диапазоне 20÷180 км/ч (рис. 5.1);

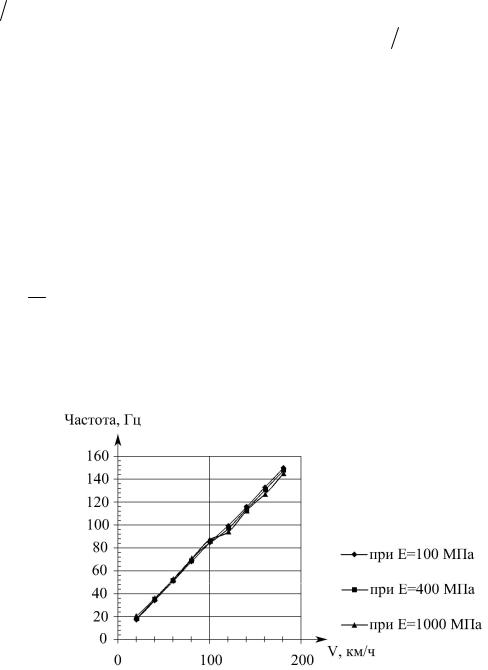
2)скорость вертикальных колебаний (рис. 5.2), ускорения колебаний (рис. 5.3) и частота (рис. 5.4) закономерно возрастают с ростом скорости в диапазоне 20÷180 км/ч;

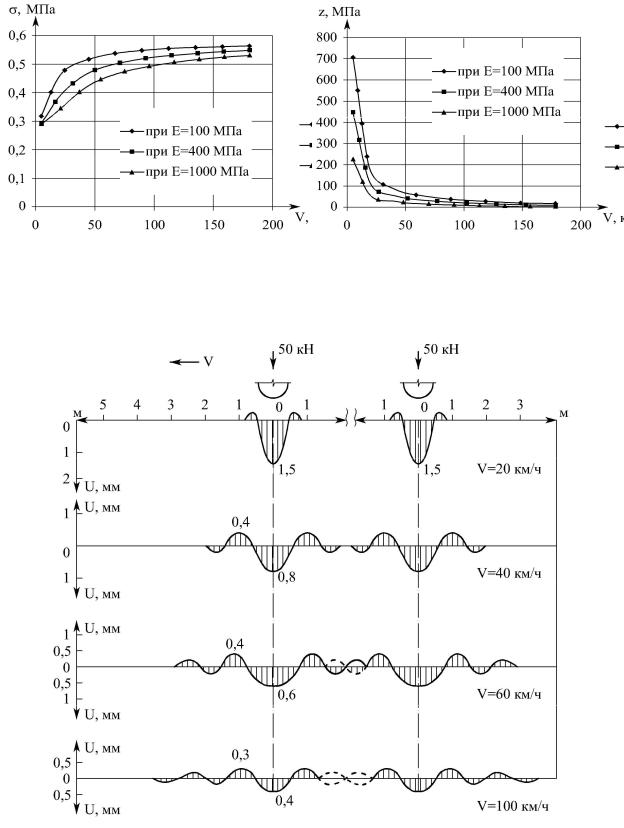
3)убывание динамического прогиба связано с увеличением напряжений сжатия упругого полупространства почти в два раза (рис. 5.5) и одновременным уменьшением длины зоны сжатия z с 700 см до 30 см, то есть почти в 23 раза;

29

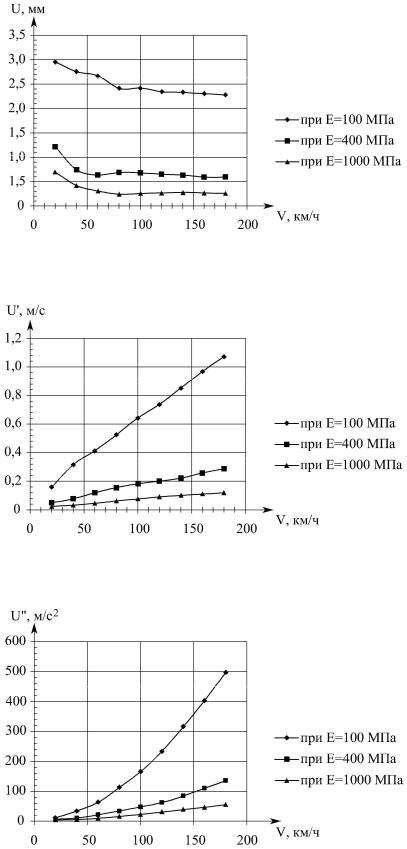
Рис. 5.1. Графики зависимости вертикальных перемещений

от скорости движения нагрузки при Е=100, 400, 1000 МПа;

Р=50 кН; =2,5 г/см3; 0 =0,01 см-1

Рис. 5.2. Графики зависимости скорости вертикальных перемещений от скорости движения нагрузки при

Е=100, 400, 1000 МПа; Р=50 кН; =2,5 г/см3; 0 =0,01 см-1

Рис. 5.3. Графики зависимости ускорения вертикальных перемещений от скорости движения нагрузки при

Е=100, 400, 1000 МПа; Р=50 кН; =2,5 г/см3; 0 =0,01 см-1

30

4)с увеличением скорости горизонтального движения нагрузки от 40 до 100 км/ч по всем направлениям от центра нагрузки формируется волновое поле (рис. 5.6);

5)параметры волнового поля: размер L, длина полуволны L0

волнообразования в однородное с равными амплитудами колебаний, то есть в виброколебания уже при скоростях движения нагрузки более

80км/ч.

Вколебательных системах наиболее содержательной является амплитудно-частотная характеристика объекта (АЧХ). Применительно к упругому полупространству, в котором при воздействии силы P возникает динамический прогиб U , а скорость перемещения силы вызывает частоту вертикальных колебаний ,

U

АЧХ= . Амплитудно-частотная характеристика полупространства

всегда стремится к минимуму с ростом скорости движения, так как

U min , а max.

Рис. 5.4. Графики зависимости частоты колебаний от скорости движения нагрузки при Е=100, 400, 1000 МПа;

Р=50 кН; =2,5 г/см3; 0 =0,01 см-1

31