2417
.pdf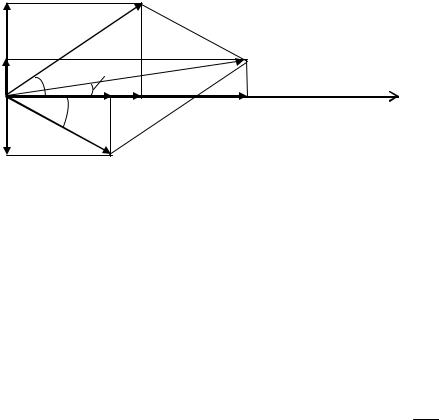
cosϕ = |
R1 |
; cosϕ |
2 |
= |
R2 |
. |
(2.50) |
|
|
||||||
1 |
Z1 |
|
|
Z2 |
|
||
|
|
|
|
|
|||
Общий ток I (до разветвления) находится как векторная сумма токов ветвей:
|
|
|
|
|
|
|
(2.51) |
I |
= I1 + I2 . |
||||||
При расчете цепи методом проводимостей ток каждой ветви условно рассматривается состоящим из двух составляющих: активной и реактивной:
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
I |
1 |
= I |
a1 |
+ I |
p1 |
|
|||||||||
|
|
|
|
|
|
|
|
|
(2.52) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
2 |
= I |
a2 |
+ I |
|
. |
|
||||||||
|
|
|
|
|
|
|
|
|
|
p2 |
|
||||
Активная составляющая тока совпадает по фазе с напряжением, реактивная составляющая тока имеет угол сдвига по фазе 90º по отношению к напряжению.
Ip2 |
I2 |
|
|
|
I |
||
|
φ |
||
Ip |
U |
||
φ2 |
|||
Ip1 |
φ1 Ia1 Ia2 |
Ia |
|
I1 |
|
||
|
|
Рис. 2.17. Векторная диаграмма для электрической цепи с двумя параллельными ветвями
На рис. 2.17 каждый вектор тока I1, I2, I разложен на активную и реактивную составляющие. Из векторной диаграммы
|
|
I |
|
= I |
|
|
cosϕ |
|
= |
U |
|
|
R1 |
=U |
R1 |
=U g |
; |
|
|
|
||||||||
|
|
a1 |
1 |
|
|
|
|
2 |
|
|
|
|||||||||||||||||
|
|
|
|
|
1 |
|
Z1 |
|
|
Z1 |
|
|
1 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z1 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
R2 |
|
|
R2 |
|
|
|
|
|
||||
|
|
I |
a2 |
= I |
2 |
cosϕ |
2 |
= |
|
|
|
=U |
=U g |
2 |
, |
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
Z2 |
|
Z2 |
|
2 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z2 |
|
|
|
|
|
||||||||
где g1 = |
R1 |
– активная проводимость первой ветви; |
g2 |
|||||||||||||||||||||||||
Z12 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
тивная проводимость второй ветви. Активная проводимость всей цепи
g = g1 + g2 .
Реактивная составляющая тока первой ветви
(2.53)
=R2 – ак-
Z22
(2.54)
50
|
|
I |
p1 |
= I |
1 |
sin ϕ |
1 |
= |
U |
|
X L1 |
=U |
X L1 |
=U b |
L1 |
, |
(2.55) |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
Z1 |
|
Z1 |
|
Z12 |
|
|
||||||
|
X L1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где bL1 = |
– реактивная проводимость первой ветви (для рассмат- |
|||||||||||||||||
Z12 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
риваемой схемы эта реактивная проводимость будет индуктивной). Реактивная составляющая тока второй ветви определяется анало-
гичным образом: |
|
||||
|
|
X C 2 |
I р2 = I2 sin ϕ2 ==U bC 2 , |
(2.56) |
|
где b |
= |
– реактивная проводимость второй ветви (для рас- |
|||
|
|||||
C 2 |
|
Z22 |
|
|
|
|
|
|
|
||
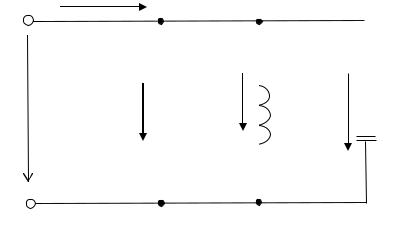
сматриваемой схемы эта реактивная проводимость будет емкостной). Эквивалентную схему, полученную в результате данного анализа, можно представить состоящей из трех параллельных ветвей (рис.
2.18).
i
u |
ia1+ia2 |
|
|
Rэ |
iL |
|
|
iC |
|
|
|
|
|
|
|||||
|
|
XLэ |
|
||||||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
ХСэ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.18. Эквивалентная схема разветвленной цепи
Параметры элементов эквивалентной схемы определяются из следующих соотношений:
Rэ = |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
; |
|
||
|
g1 |
+ g2 |
|
|||||
|
|
|
|
|||||
X Lэ |
= |
|
1 |
; |
|
(2.57) |
||
|
|
|||||||
|
|
|||||||
|
|
|
bL1 |
|
|
|||
X Cэ |
= |
|
1 |
. |
|
|
||
|
|
|
||||||
|
|
|
||||||
|
|
|
bC 2 |
|
|
|||
Реактивная составляющая общего тока
51
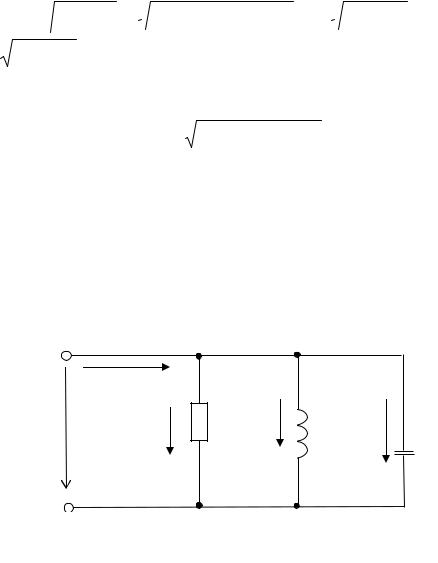
I p = I p1 +(−I p2 ) =U bL1 +(−U bC 2 ) =U [(bL1 +(−bC 2 )]. (2.58)
В общем случае активная и реактивная проводимости всей цепи определяются по формулам
g = ∑gn ; b = ∑bn , |
(2.59) |
где n – количество параллельных ветвей в цепи.
Следует иметь в виду, что при вычислении реактивной проводи-
мости емкостная проводимость по отношению к индуктивной берется с противоположным знаком.
Из векторной диаграммы ток в неразветвленной части цепи
I = 
Ia2 + I p2 =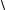 
(U g)2 +(U b)2 =U 
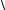g 2 +b2 =U у, (2.60)
где y = g 2 +b2 – полная проводимость всей цепи.
Таким образом, в общем случае ток в неразветвленной части це-
пи |
|
I =U (∑g)2 +(∑b)2 . |
(2.61) |
2.8. Резонанс токов
При параллельном соединении катушки индуктивности и конденсатора, когда индуктивная проводимость равна емкостной
bL=bC, (2.62)
возникает резонанс токов. В приведенной схеме (рис. 2.19) параллельно резистору включены идеальная катушка и конденсатор.
|
i |
|
|
|
u |
ia |
R |
iL L |
iC |
|
||||
|
|
|
|
C |
Рис. 2.19. Электрическая схема разветвленной цепи, иллюстрирующая резонанс токов
Выразим индуктивную и емкостную проводимости через частоту
ω:
b |
|
= |
|
1 |
; b =ω |
|
C . |
(2.63) |
|
ωрезL |
|
||||||
|
L |
|
С |
рез |
|
|
||
Произведем подстановку выражений (2.63) в уравнение (2.62):
52
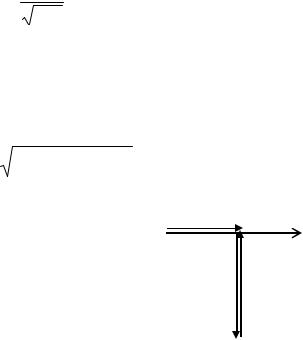
ωрезC = |
1 |
. |
(2.64) |
|
ωрезL |
||||
|
|
|
Из уравнения (2.64) определим резонансную частоту
ωрез = |
1 . |
(2.65) |
|
LC |
|
Резонанс токов, так же как и резонанс напряжений, можно получить изменением параметров L и C или изменением частоты питающего напряжения ω.
При заданном напряжении источника энергии ток в цепи пропорционален проводимости:
I =U y =U g 2 +(b |
L |
−b )2 . |
(2.66) |
|
С |
|
|
При резонансе токов с учетом равенства |
|
||
(2.62) уравнение (2.66) примет вид |
|
Ia=I |
U |
I =U g . |
|
(2.67) |
|
Резонанс токов характеризуется наименьшей величиной тока в неразветвленной части цепи, равной току в ветви с активным сопротивлением, и равенством нулю угла сдвига фаз между этим током и напряжением (рис. 2.20).
При резонансе токи в параллельных ветвях IL , IC , равные между собой по величине, но
противоположные по фазе, могут быть значительно больше общего тока I, равного активно-
му току Iа, если bL=bC>g. Это объясняется тем, что реактивные составляющие токов катушки индуктивности и конденсатора взаимно уравновешиваются и не влияют на величину общего тока (см. рис. 2.20).
При резонансе реактивные мощности Q1 (на индуктивном сопротивлении) и Q2 (на емкостном сопротивлении) равны. Реактивная
мощность всей цепи Q = QL −QC = Q1 −Q2 = 0 .
Использование резонанса токов позволяет повысить коэффициент мощности электрических установок промышленных предприятий и тем самым уменьшить реактивную мощность и связанные с ней потери.
Резонанс токов широко используется в различных радиотехнических цепях: в устройствах автоматики, телемеханики и связи.
53
2.9. Пример расчета разветвленной цепи переменного тока
Имеется разветвленная электрическая цепь (рис. 2.21).
Дано: U=127 В; f=50 Гц; R=10 Ом; L=63,7 мГн; С=212 мкФ.
Определить: I1, I2, I (токи всех участков цепи); φ1, φ2, φ (углы сдвига фаз токов относительно напряжения); S (полную мощность); Р (активную мощность); Q (реактивную мощность); построить векторную диаграмму.
|
|
|
|
|
|
|
|
(i)I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(i1) I1 |
|
|
|
|
|
|
|
|
|
(i2)I2 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
(u)U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
Рис. 2.21. Схема разветвленной электрической цепи |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1. |
Реактивные сопротивления: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|||||||||||||||||||||||
XL=ωL=314·63,7·10 |
-3 |
=20 Ом; X C |
= |
|
1 |
|
|
= |
|
|
|
10 |
|
=15 Ом. |
|||||||||||||||||||||||||||||
|
|
ωC |
|
314 |
212 |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
2. |
Полное сопротивление первой ветви |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
Z |
1 |
= |
|
R2 |
|
|
+ X 2 = 102 + 202 |
= 22,4 Ом. |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3. |
Токи в ветвях: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
I1 = |
U |
= |
|
127 |
|
|
= 5,67 |
|
|
А; I2 |
= |
|
= |
127 |
= 8,47 А. |
||||||||||||||||||||||||||
|
|
Z1 |
22,4 |
|
|
X C |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|||||||||||||||
4. |
Активная проводимость первой ветви |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
g1 |
= |
|
R |
= |
|
10 |
|
|
= 0,02 См. |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
22,42 |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
5. |
Индуктивная проводимость первой ветви |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
bL1 |
= |
|
X L |
= |
|
20 |
|
= 0,04 См. |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
22,42 |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
6. |
Емкостная проводимость второй ветви |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
b |
|
|
= |
1 |
|
= |
1 |
= 0,067 См. |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
C 2 |
|
|
|
X C |
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
7. |
Полная проводимость цепи |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
54 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
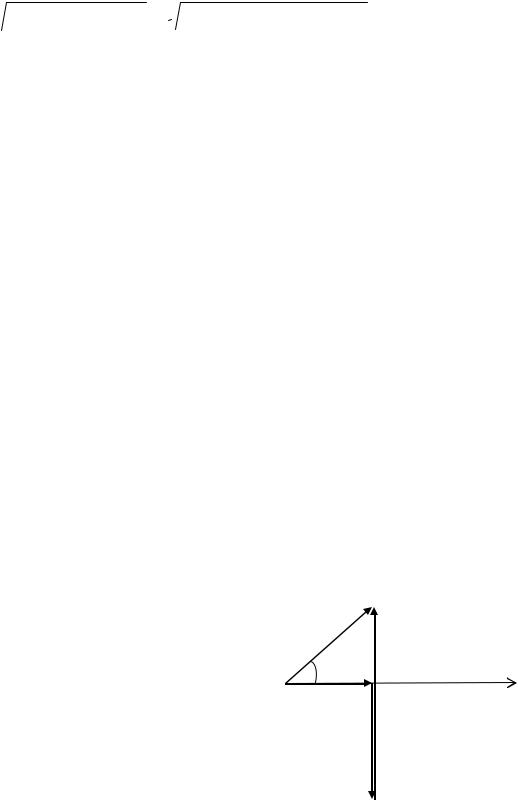
y =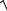 
g12 +(bL1 −bC 2 )2 = 
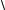0,022 +(0,04 −0,067)2 = 3,36 10−2 См. 8. Ток в неразветвленной части цепи
I=U·y=127·3,36·10-2=4,27 А. 9. Углы сдвига фаз:
|
|
ϕ = arctg |
bL1 |
= arctg |
0,04 |
= arctg2 = 64°; |
|
|
|
||||
|
|
|
|
|
|
|
|||||||
|
|
1 |
|
g1 |
0,02 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||
|
|
φ2=90º, так как ветвь чисто емкостная; |
|
|
|
||||||||
ϕ = arctg |
b |
= arctg |
bL1 −bC 2 |
= arctg |
0,04 −0,067 |
= arctg(−1,35) |
= −53°30 |
′ |
. |
||||
g |
g1 |
|
0,02 |
|
|||||||||
Знак «минус» означает, что нагрузка носит активно-емкостный характер, т.е. ток I опережает напряжение U на угол 53º30'.
10. Полная мощность
S=U·I=127·4,27=542 ВА. 11. Активная мощность
Р=S·cos φ=542·0,59=320 Вт. 12. Реактивная мощность
Q=S·sin φ=542·0,8=434 ВАр. 13. Активные и реактивные токи в ветвях:
Ia1=U·g1=127·0,02=2,54 A; Ip1=U·b1=127·0,04=5,08 A;
Ia2=0, так как во второй ветви отсутствует активное сопротивление;
Ip2=I2=8,47 A.
14. Масштабы для векторной диаграммы (рис. 34):
по напряжению m |
= 20 |
В |
; по току m |
|
= 2 |
A |
. |
|
||
|
|
|
|
|||||||
|
U |
|
см |
|
I |
|
см |
|
||
Построение |
векторной |
диа- |
|
|
|
|
|
|||
граммы следует начинать с вектора |
|
|
|
I |
|
|||||
напряжения U (см. рис. 2.22). Затем |
|
|
|
Ip2 |
|
|||||
из начала вектора напряжения про- |
|
|
φ |
U |
||||||
водится вектор тока Ia1 (активная со- |
|
|
|
Ia1 |
|
|||||
ставляющая тока первой ветви), ко- |
|
|
|
|
|
|||||
торый совпадает по направлению с |
|
|
|
|
|
|||||
вектором напряжения; из конца век- |
|
|
|
Ip1 |
|
|||||
тора Ia1 проводится вектор тока Ip1 |
|
|
|
|
|
|||||
(индуктивная |
составляющая |
тока |
|
Рис. 2.22. Векторная диаграмма |
||||||
первой ветви), |
который отстает от |
|
||||||||
напряжения на 90º; из конца вектора |
|
|
для разветвленной цепи |
|
||||||
|
|
|
|
|
||||||
Ip1 проводится вектор тока Ip2 (емкостный ток второй ветви), который опережает напряжение на 90º. Вектор тока I в неразветвленной части
55
схемы, равный сумме трех векторов токов в ветвях, проводится от начала вектора Ia1 к концу вектора Ip2. Угол φ является углом сдвига по фазе между напряжением и током в неразветвленной части схемы.
2.10. Пример расчета цепи переменного тока со смешанным соединением нагрузки
Имеется электрическая цепь (рис. 2.23).
|
|
|
|
R2 |
C2 |
|
||
|
R1 |
L1 |
|
|
|
|
|
|
a |
b |
i2(I |
|
|
c |
|||
|
|
2) |
||||||
|
|
|
|
|||||
|
i1(I1) |
L3 |
|
i3(I3) |
|
(u)U |
|
|
|
|
Рис. 2.23. Схема электрической цепи со смешанным соединением нагрузки
Дано: U=220 В; f=50 Гц; R1=3 Ом; R2=3 Ом; L1=10 мГн; L3=50 мГн; С2=400 мкФ.
Определить: токи I1, I2, I3; напряжения на участках цепи Uab, Ubc; полную мощность S; активную мощность Р; реактивную мощность Q. Построить векторную диаграмму. При решении использовать метод проводимостей.
2.10.1.Решение методом проводимостей
1.Реактивные сопротивления:
XL1=2πfL1=2·3,14·50·10·10-3=3,14 Ом;
X C 2 = |
1 |
= |
1 |
= 8 Ом; |
|
2 3,14 50 400 10−6 |
|||
|
2πfC2 |
|
||
XL3=2πfL3=2·3,14·50·50·10-3=15,7 Ом.
2. Полное сопротивление каждой ветви (каждая ветвь представляет собой последовательное соединение элементов):
Z |
1 |
= |
R2 |
+ X 2 |
= |
32 +3,142 |
= 4,34 Ом; |
|
|
|
1 |
L1 |
|
|
|
|
|
|
Z2 = |
R22 + X C2 |
2 |
= 32 +82 |
= 8,5 Ом; |
|||
|
|
|
|
|
|
|
56 |
|
Z3 =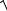 
R32 + X L23 = 
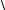02 +15,72 =15,70 Ом.
3. Для определения эквивалентного сопротивления параллельно соединенных второй и третьей ветвей найдем проводимости этих ветвей. Активные и реактивные проводимости вычисляются по формулам
g = ZR2 ; b = ZX2 .
Активная проводимость второй ветви
g2 = |
R2 |
= |
3 |
= 0,0414 См. |
|
Z22 |
8,52 |
||||
|
|
|
Реактивная (емкостная) проводимость второй ветви
b |
= |
XС2 |
= |
8 |
= 0,1105 См. |
|
|
||||
С2 |
|
Z22 |
8,52 |
|
|
|
|
|
|||
Так как активное сопротивление в третьей ветви отсутствует, ее активная проводимость g3=0.
Реактивная (индуктивная) проводимость третьей ветви
b |
= |
X L3 |
= |
15,7 |
= 0,0637 См. |
|
|
||||
L3 |
|
Z32 |
15,72 |
|
|
|
|
|
|||
Полная проводимость параллельного участка
ybc =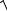 
(g2 + g3 )2 +(bL3 −bC 2 )2 =
= (0,0414 +0)2 + (0,0637 −0,1105)2 = 0,0622 См.
При сложении реактивных проводимостей емкостная проводимость по отношению к индуктивной берется со знаком «минус».
4. По найденным значениям проводимостей параллельных ветвей определим эквивалентные активное и реактивное сопротивления параллельного участка:
R |
= |
|
gbc |
= |
g2 + g3 |
= |
0,0414 + 0 |
=10,7 Ом; |
||||
|
|
|
|
|||||||||
bc |
ybc2 |
|
ybc2 |
|
0,06222 |
|
|
|||||
|
|
|
|
|
|
|
||||||
X bc = |
bbc |
|
= |
bL3 −bC 2 |
= |
|
0,0637 −0,1105 |
= −12,1 Ом. |
||||
ybc2 |
|
0,06222 |
|
|||||||||
|
|
|
ybc2 |
|
|
|
||||||
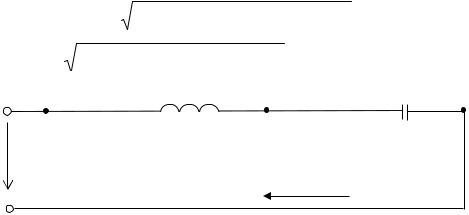
В параллельном участке цепи преобладает емкостная проводимость (сопротивление Xbc получилось со знаком «минус»), поэтому эквивалентное реактивное сопротивление будет емкостным. В результате расчета сопротивлений Rbc и Xbc эквивалентную схему можно представить как одноконтурную (рис. 2.24).
57
Эквивалентное сопротивление всей цепи |
|
|
|
|
|
|||||||||||||
|
|
Z |
экв |
= (R + R )2 |
+( X |
L1 |
− X |
bc |
)2 |
= |
|
|||||||
|
|
|
|
|
1 |
|
bc |
|
|
|
|
|
|
|
||||
= |
|
(3 +10,7)2 |
+(3,14 −12,1)2 |
=16,35 Ом. |
|
|||||||||||||
|
|
а |
|
|
|
|
|
|
b |
|
|
|
|
c |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
XL1 |
|
|
|
|
|
|
Xbc |
||||
|
R1 |
|
|
|
|
Rbc |
||||||||||||
|
u(U) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i1(I1) |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Рис. 2.24. Эквивалентная схема для расчета цепи со смешанным соединением нагрузки
5. |
Ток в неразветвленной части схемы |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
I1 = |
|
U |
= |
|
220 |
=13,45 А. |
|
|||||
|
|
|
|
|
|
|
16,35 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
Zэкв |
|
|
|
|
|
|
||||
6. |
Падения напряжений на участках цепи: |
|
|
|
||||||||||||||||
Ubc = I1Zbc = |
|
I1 |
|
= |
13,45 |
= 218 В; U ab = I1Z1 =13,45 4,34 = 58,4 В. |
||||||||||||||
ybc |
|
|
|
|||||||||||||||||
|
|
0,0622 |
|
|
|
|
|
|
|
|
|
|
||||||||
7. |
Токи в параллельных ветвях: |
|
|
|
|
|
|
|||||||||||||
|
I2 = |
Ubc |
|
= |
218 |
= 25,7 |
А; I3 |
= |
Ubc |
= |
|
218 |
=13,9 А. |
|||||||
|
Z2 |
|
|
|
15,7 |
|||||||||||||||
|
|
|
8,5 |
|
|
|
|
|
|
|
Z3 |
|
||||||||
8. Определим мощности. Полная мощность
S =U I = 220 13,45 = 2960 ВА=2,96 кВА.
Активная мощность
P =U I cosϕ = S cosϕ ,
где cosϕ = |
|
Rэкв |
= |
|
R1 + Rbc |
= |
|
3 +10,7 |
= 0,84 . |
|||||
|
Zэкв |
|
16,35 |
|||||||||||
|
|
|
|
|
Z экв |
|
|
|||||||
|
|
|
|
|
|
|
Р=2960·0,84=2490 Вт=2,49 кВт. |
|||||||
Реактивная мощность |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
Q =U I sinϕ = S sinϕ , |
|||||||
где sinϕ = |
|
X экв |
|
= |
X L1 − X bc |
|
= |
12,1−3,14 |
= −0,54 . |
|||||
|
Zэкв |
|
|
|||||||||||
|
|
|
|
Zэкв |
16,35 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
58 |
|
|||
Q=2960·(–0,54)= –1600 ВАр= –1,6 кВАр.
Построение векторной диа-
граммы (рис. 2.25) удобно начинать с параллельного участка цепи. Приняв начальную фазу напряжения Ubc равной нулю, определим углы сдвига фаз φ2 (между напря-
жением Ubc и током I2) и φ3 (между напряжением Ubc и током I3).
cosϕ2 |
= |
|
R2 |
|
= |
3 |
|
= 0,353 ; |
||
|
Z2 |
|
|
|
|
|||||
|
|
|
8,5 |
|
||||||
|
φ2=69º20'; |
|||||||||
cosϕ3 = |
R3 |
|
= |
|
0 |
|
= 0 ; φ3=90º. |
|||
Z3 |
|
15,7 |
|
|||||||
|
|
|
|
|
|
|||||
В соответствии с первым законом Кирхгофа для узла b (см.
рис. 2.23)
I1 = I2
I2
φ1 U
Uab I1 φ
φ2 |
Ubc |
φ3 |
|
I3 |
|
Рис. 2.25. Векторная диаграмма для схемы со смешанным включением нагрузки
+ I3 ,
то есть вектор тока I1 равен сумме векторов токов I2 и I3.
Определим угол φ1 сдвига по фазе между током I1 и напряжением Uab на последовательном участке.
cosϕ = |
R1 |
= |
3 |
= 0,692 ; φ1=46º15'. |
|
|
|||
1 |
Z1 |
|
4,34 |
|
|
|
|
Так как нагрузка на этом участке активно-индуктивная, то напряжение Uab будет опережать по фазе ток I1 на угол φ1.
В соответствии со вторым законом Кирхгофа (см. рис. 2.23)
U =U ab +Ubc ,
то есть вектор напряжения U равен сумме векторов напряжений Uab и
Ubc.
Угол сдвига по фазе между напряжением U и током I1 можно определить из построенной в масштабе векторной диаграммы, а также по параметрам эквивалентной схемы (см. рис. 2.24)
cosϕ = |
Rэкв |
= |
|
13,7 |
= 0,84 ; φ=32º45'. |
|
Zэкв |
16,35 |
|||||
|
|
|
||||
59