
2417
.pdf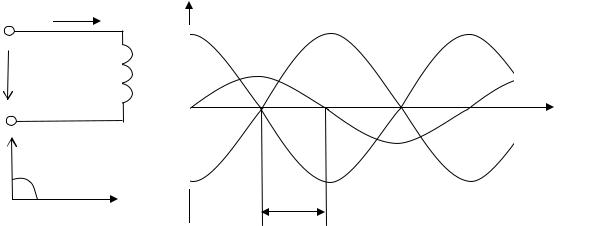
i |
u, i, e |
|
|
|
|
u |
|
u |
L |
i |
ωt |
|
|
|
|
U |
|
|
eL |
90° |
I |
|
|
|
|
||
|
|
90° |
|
|
|
|
Рис. 2.6. Электрическая схема, графики изменения напряжения, тока, ЭДС самоиндукции и векторная диаграмма для цепи с индуктивным элементом
Так как |
di |
|
d (Imsinωt) |
|
|
||
eL = −L |
= −L |
= −Im Lωcosωt , |
(2.12) |
||||
dt |
dt |
|
|||||
то |
|
|
|
||||
|
|
|
|
|
|
||
u = Im Lωcosωt =U mcosωt =U msin(ωt +90°). |
(2.13) |
||||||
Из выражений (2.12) и (2.13) видно, что в цепи с индуктивным элементом ток отстает от напряжения по фазе на угол 90º (π/2), а
согласно выражению (2.11) ЭДС находится в противофазе с приложенным напряжением (см. рис. 2.6).
Катушка в цепи переменного тока оказывает этому току сопро-
тивление, которое называется индуктивным и обозначается ХL. |
|
||||
X L =ωL = 2πfL . |
(2.14) |
||||
В системе СИ сопротивление X L измеряется в омах (Ом). |
|
||||
Математическое выражение закона Ома для этой цепи |
|
||||
I = |
U |
. |
|
|
(2.15) |
|
|||||
|
X L |
|
|||
Мгновенная мощность для цепи с индуктивным сопротивлением |
|||||
р = u i =U msin(ωt +90°) Imsinωt = |
1 |
U m Imsin2ωt . |
(2.16) |
||
|
|||||
2 |
|
|
|||
Из рис. 2.7 видно, что при одинаковых знаках напряжения и тока мгновенная мощность положительна, а при разных знаках – отрицательна. Это означает, что мощность в первую четверть периода забирается из сети и запасается в магнитном поле катушки, а в следую-
40
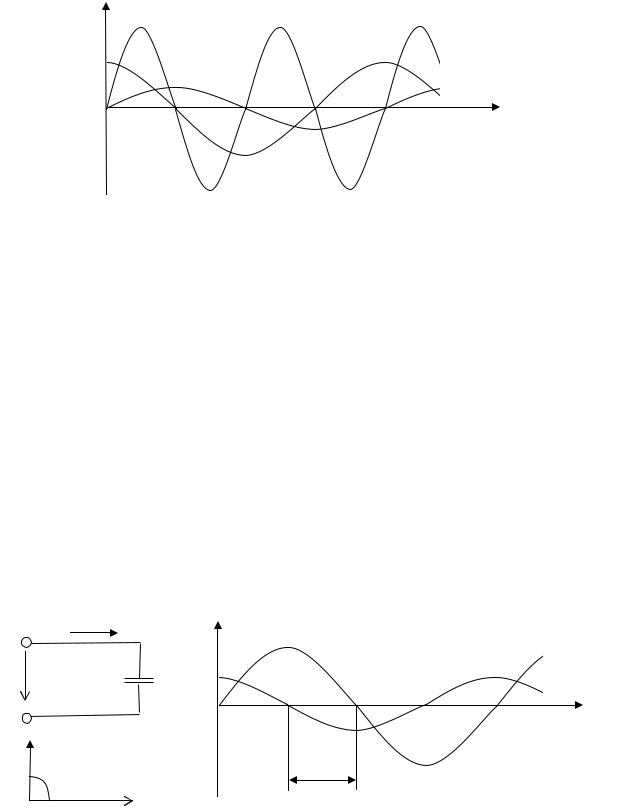
щую четверть периода возвращается в сеть, т.е. происходит перекачивание энергии от источника к потребителю и обратно.
u, i, p
p
u
i |
ωt |
Рис. 2.7. Графики изменения напряжения, тока и мощности в цепи с индуктивным сопротивлением
Для количественной характеристики интенсивности обмена энергией между источником и катушкой служит реактивная мощность
QL = I 2 X L . |
(2.17) |
Размерностью этой мощности является вольт-ампер реактивный
(ВАр).
Энергия, запасаемая в магнитном поле катушки, зависит от индуктивности катушки и от величины протекающего через нее тока
WL = |
L I 2 |
. |
(2.18) |
|
2 |
||||
|
|
|
2.3.3. Цепь переменного тока с емкостным элементом
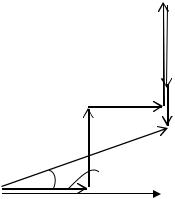
На рис. 2.8 приведена схема цепи переменного тока с емкостным элементом (конденсатором).
I(i) |
|
u, i |
|
|
|
u |
|
U |
C |
i |
ωt |
|
|
|
I |
90º |
90º |
|
U |
Рис. 2.8. Электрическая схема, графики изменения напряжения, тока и векторная диаграмма для цепи с емкостным элементом
41
Под действием синусоидального напряжения u =Umsinωt в цепи с емкостным элементом протекает ток
i = |
dq |
= C |
du |
= C |
d (Umsinωt) |
=UmCωcosωt = |
(2.19) |
|
dt |
dt |
dt |
|
|||||
|
|
|
|
|
||||
|
=U mCωsin(ωt +90°) |
= Imsin(ωt +90°), |
|
|||||
где С – емкость; q – заряд на электродах емкостного элемента.
Из выражения (2.19) видно, что в цепи с емкостным элементом ток опережает по фазе напряжение на угол 90º (π/2) (см. рис. 2.8).
В цепи переменного тока емкостный элемент обладает сопротивлением, которое называется емкостным и обозначается ХС.
X C = |
1 |
|
= |
1 |
. |
(2.20) |
|
|
|
|
2π f С |
||||
ωС |
|
|
|
||||
В системе СИ сопротивление X C измеряется в омах (Ом). |
|
||||||
Математическое выражение закона Ома для этой цепи |
|
||||||
I = |
U |
|
. |
|
(2.21) |
||
X C |
|
|
|||||
|
|
|
|
|
|
||
Мгновенная мощность в цепи с емкостным сопротивлением будет в противофазе с мгновенной мощностью в цепи с индуктивным элементом
р = −u i = −U msinωt Imsin(ωt +90°)= − |
1 |
U m Imsin2ωt. (2.22) |
|
2 |
|||
|
|
Анализ приведенных формул показывает, что в цепи с емкостью (как и в цепи с индуктивностью) мощность в первую четверть периода забирается из сети и запасается в электрическом поле конденсатора, а в следующую четверть периода возвращается в сеть. Для количественной характеристики интенсивности обмена энергией между источником и конденсатором служит реактивная мощность
Q = I 2 X |
C |
. |
(2.23) |
|
C |
|
|
|
|
Энергия, запасаемая в электрическом поле конденсатора, |
|
|||
W = |
C U |
2 |
. |
(2.24) |
|
|
|||
C |
2 |
|
|
|
|
|
|
|
|
2.4. Анализ неразветвленной цепи переменного тока
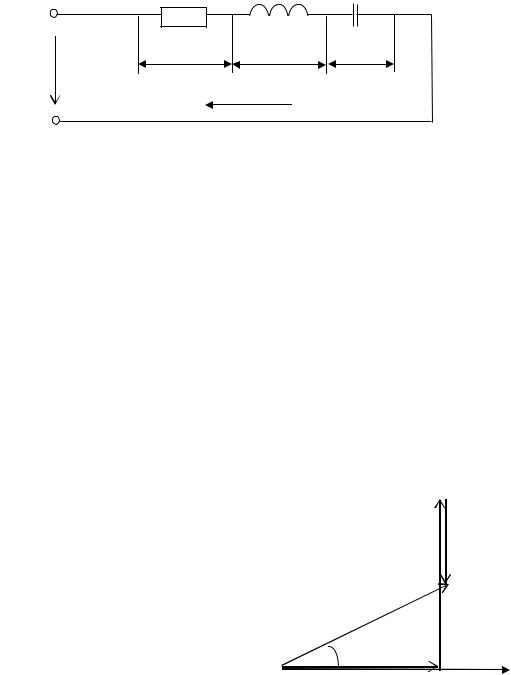
Цепь с активным сопротивлением, индуктивностью и емкостью представляет собой общий случай последовательного соединения активных и реактивных сопротивлений (рис. 2.9).
42
R |
XL |
XC |
|
|
|
Ua |
UL |
UC |
u(U) |
i(I) |
|
Рис. 2.9. Последовательное соединение активного, индуктивного и емкостного сопротивлений
При прохождении тока в цепи на каждом элементе возникает падение напряжения:
U a = I R; |
|
|
(2.25) |
U L = I X L ; |
|
|
|
UC = I X C . |
|
Для каждого элемента цепи угол сдвига по фазе между током и напряжением имеет свое значение. Вектор приложенного к схеме напряжения U определится как сумма векторов напряжений на отдельных элементах схемы. Для рассматриваемой одноконтурной схемы в соответствии со вторым законом Кирхгофа справедливо уравнение
|
|
|
|
|
|
|
|
|
|
|
U |
=U a +U L +UC . |
(2.26) |
||||||||
Для анализа работы данной цепи |
|
|
|
|
||||||
построим векторную диаграмму (рис. |
|
|
|
|
||||||
2.10). Перед построением выбирается |
|
|
UL |
UC |
||||||
масштаб для тока и напряжения. По- |
|
|
|
|
||||||
строение векторной диаграммы начи- |
|
|
U |
|
||||||
нают с вектора той величины, которая |
|
|
|
|||||||
является общей для всех элементов |
|
|
φ Ua |
I |
||||||
цепи. В данном случае при последо- |
|
|
||||||||
вательном соединении общей вели- |
Рис. 2.10. Векторная диаграмма |
|||||||||
чиной для всех элементов цепи явля- |
||||||||||
ется ток. Поэтому первым проводим |
|
для схемы, состоящей из |
||||||||
последовательно соединенных |
||||||||||
вектор тока. Вектор напряжения на |
||||||||||
активном сопротивлении совпадает |
|
активного, индуктивного |
||||||||
и емкостного сопротивлений |
||||||||||
по фазе с вектором тока. Вектор напряжения на индуктивном сопротивлении опережает вектор тока на
угол 90º, а вектор напряжения на емкостном сопротивлении отстает от вектора тока на угол 90º.
43
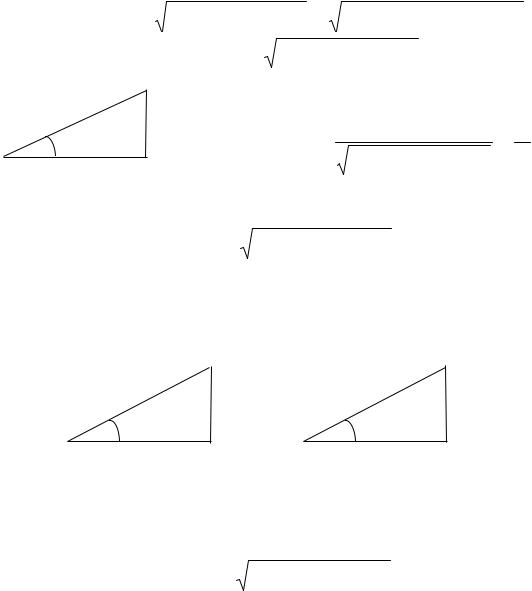
Знак перед углом сдвига фаз ϕ зависит от режима цепи. Если в рассматриваемой цепи преобладает индуктивное сопротивление, то
U L >U C . |
(2.27) |
В этом случае нагрузка имеет активно-индуктивный характер, |
|
а напряжение U опережает по фазе ток I (угол ϕ положительный). |
|
Если в цепи преобладает емкостное сопротивление, то |
|
U L <U C . |
(2.28) |
В этом случае нагрузка имеет активно-емкостный характер, а напряжение U отстает по фазе от тока I (угол ϕ отрицательный).
Выделим из векторной диаграммы треугольник напряжений (рис.
23), из которого следует: |
|
|
|
|
|
U = U a2 +(U L −UC )2 = I 2 R2 +(I X L |
− I X C )2 = |
(2.29) |
|||
= I R2 +(X L − X C )2 . |
|
|
|||
|
|
|
|||
U |
Закон Ома |
для |
неразветвленной |
||
цепи запишется в виде |
|
|
|||
UL–UC=UP |
|
|
|||
φ Ua |
I = |
U |
= U , |
(2.30) |
|
Рис. 2.11. Треугольник |
R2 +(X L − X C )2 |
Z |
|
||
где Z – полное |
сопротивление |
нераз- |
|||
напряжений |
ветвленной цепи, |
|
|
|
|
|
|
|
|
||
Z = |
R2 +(X L − X C )2 . |
|
|
|
(2.31) |
Если стороны треугольника напряжений разделить на силу тока, получится треугольник сопротивлений; если стороны треугольника напряжений умножить на силу тока, получится треугольник мощно-
стей (рис. 2.12).
Z |
S |
XL–XC=X |
QL–QC=Q |
φ R |
φ P |
Рис. 2.12. Треугольники сопротивлений и мощностей
Из приведенных треугольников можно записать уравнения, которые широко используются при анализе электрических цепей.
Из треугольника сопротивлений:
Z = R2 +(X L − X C )2 ; |
(2.32) |
||||
cosϕ = |
R |
; sinϕ = |
X |
. |
(2.33) |
Z |
|
||||
|
|
Z |
|
||
|
|
44 |
|
|
|

Из треугольника мощностей: |
|
|
|
|
S = IU , |
|
|
|
(2.34) |
или |
|
|
|
|
S = P2 +Q2 = P2 +(Q |
L |
−Q )2 |
, |
(2.35) |
|
C |
|
|
где S – полная мощность; Р – активная мощность; Q – реактивная мощность.
Размерность полной мощности – вольт-ампер (ВА); размерность активной мощности – ватт (Вт); размерность реактивной мощности – вольт-ампер реактивный (ВАр).
Величина cos φ называется коэффициентом мощности цепи.
cosϕ = |
P |
. |
(2.36) |
||
|
|
||||
|
|
S |
|
||
P = S cosϕ = IU cosϕ. |
(2.37) |
||||
sinϕ = |
Q |
. |
(2.38) |
||
|
|||||
|
S |
|
|||
Q = S sinϕ = IU sinϕ . |
(2.39) |
||||
Полное сопротивление может быть представлено комплексным числом в алгебраической и показательной форме. Комплекс полного сопротивления в алгебраической форме
Z& = R + j( X L − X C ), |
(2.40) |
||
где j – мнимая единица ( j2 = −1). |
|
||
Комплекс полного сопротивления в показательной форме |
|
||
Z& = Z e jϕ , |
(2.41) |
||
где Z = R2 +( X L − X C )2 ; ϕ = arctg |
X L − X C |
. |
|
|
|
||
|
R |
|
|
2.5.Резонанс напряжений
Взамкнутом контуре электрической цепи (см. рис. 21), содержащей активное сопротивление R, индуктивность L и емкость С, при условии равенства реактивных сопротивлений
X L = X C |
|
(2.42) |
|
возникает резонанс напряжений. |
|
|
|
Выразим XL и XC через частоту ω и подставим в равенство (2.42). |
|||
ωрезL = |
1 |
, |
(2.43) |
ωрезС
откуда
45
ωрез = |
1 |
=ω0 , |
(2.44) |
|
LC |
|
|
где ωрез – частота питающего напряжения; ω0 |
– частота собственных |
||
колебаний LC-контура.
Резонанс напряжений возникает в том случае, когда частота питающего напряжения равна частоте собственных колебаний LC- контура.
Следовательно, добиться резонанса напряжений можно изменением частоты ωрез или параметров контура L и C.
При резонансе напряжений |
|
|
|
|
||
I = U |
= |
U |
= U |
= U |
, |
(2.45) |
Z |
|
R2 +( X L − X C )2 |
R2 +0 |
R |
|
|
т.е. полное сопротивление цепи становится минимальным и равным
|
только активному сопротивлению. Следова- |
UL |
тельно, ток при резонансе напряжений мак- |
|
симальный. |
|
|
При резонансе напряжений (рис. 2.13) |
|
UС |
|
U L =UC . |
(2.46) |
Ua=U |
I |
Если при этом |
|
|
X L = X C > R , |
(2.47) |
|
|
|
||
то напряжение на участке с индуктивным сопротивлением и равное ему напряжение на участке с емкостным сопротивлением будут больше питающего напряжения U.
Из векторной диаграммы (см. рис. 2.13) видно, что при резонансе напряжение U, приложенное к цепи, оказывается равным напряжению на активном сопротивлении (U=Uа) и совпадает по фазе с током I, т.е. угол сдвига фаз между I и U равен нулю (φ=0).
2.6. Пример расчета неразветвленной цепи переменного тока
Имеется неразветвленная (одноконтурная) цепь переменного то-
ка (рис. 2.14).
Дано: R1=2 Ом; R2=2 Ом; XL1=4 Ом; XL2=5 Ом; XС1=4 Ом; XС2=2 Ом; U=220 B.
Определить: Z (полное сопротивление цепи), cos φ, sin ϕ , S (пол-
ную мощность), Р (активную мощность), Q (реактивную мощность), I (ток цепи). Построить в масштабе векторную диаграмму.
46
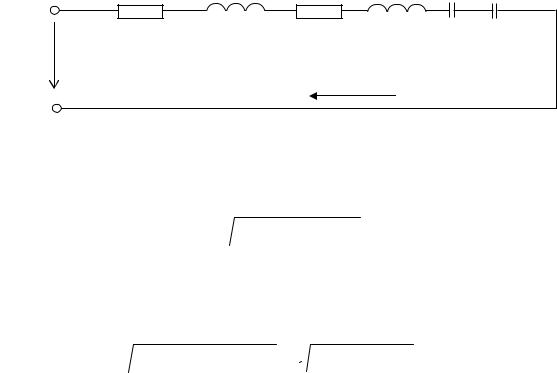
R1 |
X |
R2 |
XL2 |
X |
XC2 |
|
L1 |
|
C1 |
||
u(U) |
|
|
|
|
|
|
|
|
i(I) |
|
|
Рис. 2.14. Неразветвленная цепь переменного тока |
|
||||
Решение.
1. Определим полное сопротивление цепи по формуле
Z = 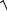 R2 +( X L − X C )2 ,
R2 +( X L − X C )2 ,
где R=R1+R2=2+2=4 Ом – арифметическая сумма всех активных со-
противлений; XL=XL1+XL2=4+5=9 Ом; XС=XС1+XС2=4+2=6 Ом – соот-
ветственно арифметические суммы однотипных реактивных (индуктивных и емкостных) сопротивлений.
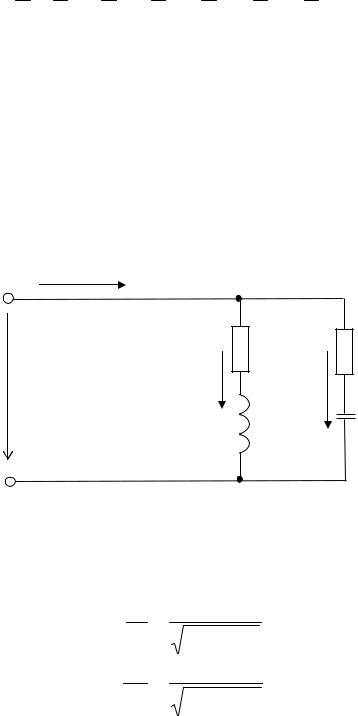
Z = 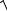 R2 +( X L − X C )2 =
R2 +( X L − X C )2 = 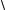 42 +(9 −6)2 = 5 Ом.
42 +(9 −6)2 = 5 Ом.
2. Вычислим ток по закону Ома для цепи переменного тока:
I = |
U |
= |
220 |
= 44 Α. |
|
Z |
5 |
||||
|
|
|
3. Из треугольника сопротивлений определим:
cos φ= |
R |
= |
4 |
= 0,8; sin φ= |
X L − X C |
= |
9 −6 |
= |
3 |
= 0,6 . |
|
Z |
5 |
Z |
5 |
5 |
|||||||
|
|
|
|
|
|
По значениям тригонометрических функций найдем величину угла сдвига фаз:
φ=36º50′.
4.Полная мощность S=U·I=220·44=9680 ВА=9,680 кВА.
5.Активная мощность P = S cos φ=9680·0,8=7744 Вт=7,744 кВт.
6.Реактивная мощность Q=S·sinφ=9680·0,6=5808 ВАр=5,808
кВАр.
При построении векторной диаграммы тока и напряжений следует исходить из следующих условий:
1) через все сопротивления протекает одинаковый ток, так как схема одноконтурная;
2) на каждом сопротивлении создается падение напряжения, величина которого определяется по закону Ома для участка цепи:
–на активном сопротивлении Ua=I·R;
–на индуктивном сопротивлении UL=I·XL;
–на емкостном сопротивлении UС=I·XС.
47
Построение векторной диаграммы.
1. Зная величину тока (I=44 A), определим падения напряжения на всех сопротивлениях:
U L1 = I X L1 = 44 |
4 =176 Β; |
U a1 = I R1 = 44 2 = 88 В; |
|
U L2 = I X L2 = 44 |
5 = 220 Β; |
U a2 = I R2 |
= 44 2 = 88 B; |
UC1 = I X C1 = 44 4 =176 B; |
UC 2 = IC 2 |
= 4 2 = 88 B. |
|
2. Исходя из размеров бумаги (миллиметровка или тетрадный лист в клеточку), задаем масштаб по току и напряжению. Для рас-
сматриваемого примера принимаем: масштаб по току mI |
=10 А/см, |
|||||||||||||||||||||||||||||||||||
масштаб по напряжению mU = 44 В/см. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
Длина вектора тока |
|
|
|
|
|
|
44 А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
lI |
= I / mI |
= |
|
|
|
|
= 4,4 см. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
10 А/см |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Длины векторов напряжений: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
l |
UL1 |
=U |
L1 |
/ m |
= |
176 Β |
|
|
= 4 см |
; |
l |
Ua1 |
=U |
a1 |
/ m |
|
= |
|
|
88 Β |
|
|
|
|
= 2 см; |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
U |
|
44 В/ см |
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
|
|
44 В/ см |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
l |
UL2 |
=U |
L2 |
/ m |
= |
220 Β |
|
= 5 см |
; |
l |
Ua2 |
=U |
a |
2 |
/ m |
|
|
= |
|
88 Β |
|
|
|
|
= 2 см; |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
U |
|
44 Β/ см |
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
|
|
44 Β/ cм |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
UC1 |
=U |
C1 |
/ m |
= |
|
|
|
|
176 Β |
|
|
= 4 см; |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
UL2 |
|
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
44 Β/ cм |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
UC1 |
|
|
|
lUC 2 =UС2 |
/ mU |
|
= |
|
|
|
88 Β |
|
|
|
= 2 см. |
||||||||||||
|
|
|
|
|
|
|
Ua2 |
|
|
|
|
|
44 Β/ cм |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
UC2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
UL1 |
|
|
|
|
|
|
|
3. Выполняем построение диа- |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
U |
|
|
|
граммы в следующей последователь- |
||||||||||||||||||||||||
|
|
|
|
φ |
Ua1 |
I |
|
|
|
ности: |
|
|
|
|
|
|
|
вектор тока (рис. |
||||||||||||||||||
Рис. 2.15. Векторная диаграмма |
|
|
|
|
–проводим |
|||||||||||||||||||||||||||||||
2.15); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
для неразветвленной цепи |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
–проводим векторы напряжений на каждом сопротивлении с учетом сдвига фаз относительно вектора тока, при этом следует придерживаться последовательности расположения сопротивлений на схеме
(см. рис. 2.14):
Ua1 →U L1 →Ua2 →U L2 →UC1 →UC 2 ;
48
|
|
|
|
находим сложением векторов, |
для чего |
|||
–вектор напряжения U |
||||||||
начало принятого за |
|
|
|
|
|
концом |
||
|
первый вектор Ua1 соединяем с |
|||||||
последнего вектора |
|
|
|
|
||||
UC 2 : |
|
|||||||
U =U a1 +U L1 +U a2 +U L2 +UC1 +UC 2 .
Угол φ является углом сдвига фаз между током и общим (приложенным) напряжением.
2.7. Анализ разветвленной цепи переменного тока методом проводимостей
Для расчета разветвленных цепей с большим числом ветвей обычно пользуются методом проводимостей. Проводимость измеряется в сименсах (См). Эта единица измерения является обратной по отношению к ому (Ом).
|
i(I) |
|
|
R1 |
R2 |
|
|
|
u(U) |
i1(I1) |
i2(I2) |
|
XL1 |
XC2 |
Рис. 2.16. Электрическая цепь с двумя параллельными ветвями
Токи в параллельных ветвях (рис. 2.16) определяются по закону Ома:
I1 = |
U = |
R2 |
U |
; |
(2.48) |
|
Z1 |
+ X 2 |
|
|
|
|
|
1 |
L1 |
|
|
I2 = |
U = |
R22 |
U |
. |
(2.49) |
|
Z2 |
+ X C21 |
|
|
Вектор тока I1 первой ветви отстает от вектора напряжения на угол ϕ1 , а вектор тока I2 второй ветви опережает вектор напряжения на угол ϕ2 .
Углы сдвига фаз можно определить исходя из соотношений:
49
