
2417
.pdfAD–BC=1. |
|
(4.7) |
|
Если четырехполюсник симметричный, то A=D. |
|
||
При питании четырехполюсника со стороны выходных зажимов |
|||
после несложных преобразований получаем уравнения |
|
||
U&1 = AU&2 + BI&2 , |
U&2 = DU& |
1 + BI&1′, |
(4.8) |
|
I&2′ = CU&1 |
|
|
I&1 = CU&2 + DI&2 , |
+ AI&1′, |
|
|
т.е при замене входных и выходных зажимов и выбранных положительных направлениях токов (см. рис. 4.12,г) в основных уравнениях четырехполюсника коэффициенты A и D меняются местами.
Коэффициенты A, B, C, D четырехполюсника опытным путем проще и точнее определять, если измерять входные сопротивления со стороны первичных и вторичных зажимов в режимах холостого хода
и |
|
короткого |
|
замыкания |
Z1x , |
Z1к, |
|
Z2 x , |
Z2к , |
учитывая, |
что |
||||||||||||||||||||||||||||||||||||||||
Z |
1 |
= U&1 = |
|
AU&2 + BI&2 , Z |
2 |
= U&2 = DU&1 + BI&1′ : |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
I&1 |
|
|
CU&2 + DI&2 |
|
|
|
|
I&2′ |
|
|
|
|
|
CU&1 + AI&1′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
Z |
1x |
= |
U&1x |
= z |
|
e jϕ1x |
= |
|
A |
|
; Z |
1к |
= |
|
U&1к |
= z |
e jϕ1к |
= |
B |
; |
|
(4.9) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
& |
|
|
1x |
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
& |
|
|
|
|
1к |
|
|
|
D |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
I1x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I1к |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
U& |
|
|
|
|
|
jϕ |
|
|
|
|
|
D |
|
|
|
|
|
|
|
U& |
|
|
jϕ |
|
|
B |
|
|
|||||||||||||||
|
|
|
|
|
Z2 x |
= |
2 x |
|
= z2 xe |
|
|
2 x |
= |
|
|
|
|
|
|
; Z2к = |
|
|
2к |
|
|
= z2кe |
|
2к = |
|
|
. |
(4.10) |
|||||||||||||||||||
|
|
|
|
|
& |
|
|
|
C |
& |
|
A |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
I2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I2к |
|
|
|
|
|
|
|
||||||||||||||
|
|
Из последних четырех уравнений только три являются независи- |
|||||||||||||||||||||||||||||||||||||||||||||||||
мыми, в чем легко убедиться, если составить отношения: |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z1x |
|
= |
AD |
|
и |
Z2 x |
= |
DA |
. |
|
|
|
|
|
|
|
(4.11) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z1к |
CB |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z2к |
|
|
CB |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
Отсюда следует, что для всякого линейного пассивного четырех- |
|||||||||||||||||||||||||||||||||||||||||||||||||
полюсника |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z1x |
|
|
Z2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
. |
|
|
|
|
|
|
|
|
(4.12) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z1к |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z2к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Поэтому для вычисления четырех коэффициентов (A, B, C, D) нужно взять любые три из четырех соотношений (4.9), (4.10) и воспользоваться уравнением (4.7).
Решая эту систему из четырех уравнений относительно коэффициентов четырехполюсника, получаем
A = |
Z1x |
; B = |
Z2 x Z1к |
; C = |
1 |
и D = |
Z2 x |
, |
(4.13) |
|
|
Z |
|
||||||
|
Z |
Z |
|
Z |
|
||||
где
110
Z = ( Z1x −Z1к )Z2к . |
(4.14) |
Таким образом, коэффициенты линейного пассивного четырехполюсника не зависят от его напряжений и токов, а определяются только сопротивлениями входящих в него элементов.
4.7.3.Расчет режима работы трехполюсника
вцепи постоянного тока
Рассмотрим расчет нелинейных резистивных трехполюсников (транзисторов, электронных ламп) в режимах, характерных для их работы в схемах усилителей.
Рассмотрим типовое включение нелинейных трехполюсников в цепь постоянного тока. На рис. 4.14 приведены схема включения трехполюсника и вольт-амперные характеристики его входной и вы-
ходной цепей (I1=f1(U1) при U2=const и I2=f2(U2) при I1=const).
|
R1 |
I1 |
|
I2 |
R2 |
|
|
|
|
||
E1 |
|
1 |
|
2 |
E2 |
|
|
|
|
||
|
U1 |
П |
|
U2 |
|
|
|
1' |
2' |
|
|
|
|
|
а |
|
|
I1 |
U2п U2>U2п |
I2 |
|
|
|
U2<U2п |
Е2 |
|
I1>I1п |
||
Е1 |
|
|
|
||
R1 |
|
|
R |
|
I1п |
|
|
|
2 |
A |
|
|
|
|
I2п |
|
|
I1п |
A |
|
|
I1<I1п |
|
|
|
|
|||
0 |
|
U1 |
|
|
U2 |
U1п |
E1 |
0 |
U2п |
E2 |
|
|
б |
|
|
|
в |
Рис. 4.14. Схема включения трехполюсника (а) и вольт-амперные характеристики его входной (б) и выходной (в) цепей
111

На семействе вольт-амперных характеристик строятся нагрузочные характеристики со стороны входа и со стороны выхода трехполюсника (см. рис. 4.14,б,в) .
Уравнение нагрузочной характеристики со стороны входа трехполюсника
U1 = Е1 − I1R1 . |
(4.15) |
Уравнение нагрузочной характеристики со стороны выхода трехполюсника
U 2 = Е2 − I2 R2 . |
(4.16) |
Точки пересечения нагрузочных характеристик со статическими вольт-амперными характеристиками являются рабочими точками трехполюсника при соответствующих напряжениях U2 на входной характеристике и токах I1 на выходной характеристике. Режим в цепи постоянного тока называется режимом покоя, так как рабочий режим трехполюсника определяет одна точка А (см. рис. 4.14,б,в).
4.7.4. Расчет режима работы трехполюсника для переменных составляющих напряжений и токов
Во многих цепях с трехполюсниками, кроме источников постоянных ЭДС, определяющих режим покоя, действует источник переменной ЭДС е (рис. 4.15). При этом на входе и выходе трехполюсника токи и напряжения будут иметь и постоянные Iп, Uп и переменные i, u составляющие. Положение рабочей точки А на вольт-амперной характеристике трехполюсника, определяющей постоянные составляющие тока и напряжения, в общем случае зависит от значений как постоянных ЭДС Е1 и Е2, так и от переменной ЭДС е.
|
R1 |
I1п+i1 |
|
|
I2п+i2 |
R2 |
||
|
|
|
||||||
|
|
1 |
|
|
2 |
|
|
|
e |
|
|
|
|||||
|
|
|
|
|
|
|
||
|
|
U1п+u1 |
П |
|
U2п+u2 |
|
E2 |
|
|
|
|
|
|
||||
E1 |
|
|
|
|
|
|
|
|
1' |
2' |
|
|
|
|
|||
|
|
|
|
|
|
|||
Рис. 4.15. К расчету режима трехполюсника для переменных составляющих напряжений и токов
112
В большинстве практических случаев, например, в цепях с транзисторами, положение начальной рабочей точки можно считать соответствующим режиму покоя, т.е. определять при е=0.
Сизменением на входе трехполюсника переменных составляю-
щих тока i1 и напряжения u1 (с изменением е) изменяются ток i2 и напряжение u2 в выходной цепи трехполюсника.
Сизменением переменной ЭДС е со стороны входа происходит
изменение тока во входной цепи (I1п+i1), что ведет к изменению тока в выходной цепи (I2п+i2), а, следовательно, напряжение (U1п+u1) изменяется пропорционально изменению сигнала на входе.
Для анализа рассматриваемой цепи обычно используют сочета-
ние вольт-амперной характеристики I1=f1(U1) при заданном U2 и I2=f2(U2) при заданном значении I1 и по нагрузочным характеристикам определяют пределы изменения соответствующих параметров. Такой анализ удобно использовать при работе транзисторов в усилительных каскадах. При этом можно использовать соотношения
u1=h11·i1+h12·u2; |
(4.17) |
i2=h21·i1+h22·u2, |
(4.18) |
где h11, h12, h21, h22 – постоянные параметры, соответствующие конкретному транзистору:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
h11 |
dU1 |
|
|
|
; h12 |
dU1 |
|
|
|
|
; |
(4.19) |
|||||||||
= |
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
dI1 |
|
|
U |
2 |
=const |
dU 2 |
|
|
I |
|
=const |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
h21 |
dI2 |
|
|
|
|
; h22 |
dI2 |
|
|
|
|
. |
(4.20) |
||||||||
= |
|
|
|
|
|
|
= |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
dI1 |
|
|
|
=const |
dU 2 |
|
I |
=const |
|
|||||||||||
|
|
|
|
|
|
U |
2 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
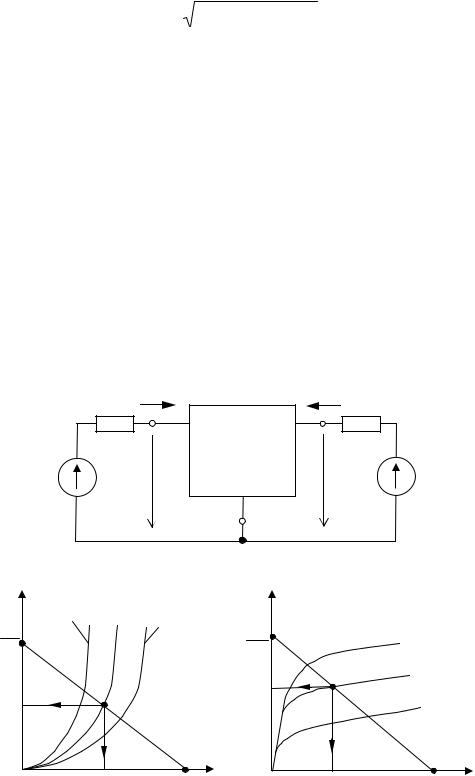
Параметры h11, h12, h21, h22 нелинейного трехполюсника рассчитываются по соответствующим вольт-амперным характеристикам.
Контрольные вопросы
1. При заданной вольт-амперной характеристике статическое сопротивление нелинейного элемента в точке А составляет:
1) |
20 Ом; |
U, В |
А |
|
2) |
10 Ом; |
30 |
|
|
3) |
30 Ом; |
20 |
|
|
10 |
|
|
||
4) |
5 Ом. |
|
|
|
0 |
|
|
||
|
|
|
I, А |
|
|
|
1 |
2 3 |
113
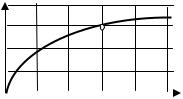
2. Диоды D1 и D2 имеют ВАХ, изображенные на рисунке. U=2 В, I1=1 А. Тогда сопротивление резистора R будет равно:
I1 |
D1 |
|
|
|
|
|
|
||
R |
|
|
|
|
I |
D2 |
|
1) 0,25 Ом; |
|
|
|
|||
+ |
U |
|
||
– |
2) 1,5 Ом; |
|||
|
||||
D2 |
D1 |
|
3) 1 Ом; |
|
I, А |
|
|
4) 0,75 Ом. |
|
3 |
|
|
||
|
|
|
||
2 |
|
|
|
|
1 |
|
|
|
|
0 |
1,5 2 |
U, В |
|
|
0,5 1 |
|
3. При заданной вольт-амперной характеристике дифференциальное сопротивление Rдиф в точке а равно:
|
|
|
|
|
|
U |
|
|
|
|
|
|
|
|
|
|
|
|
U1 |
|
a |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β |
α |
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
I1 |
|
|
|
1) |
∆U |
= |
|
mU |
|
tg(180°− β) ; 2) |
∆U |
= |
mU |
tgα ; 3) |
U1 |
; |
∆I |
∆I |
|
||||||||||
|
|
|
|
|||||||||
|
|
|
mI |
|
mI |
I1 |
||||||
4) |
∆U |
= |
mU |
tgβ . |
|
|
|
|
|
|
||
∆I |
|
|
|
|
|
|
|
|||||
|
|
|
mI |
|
|
|
|
|
|
|||
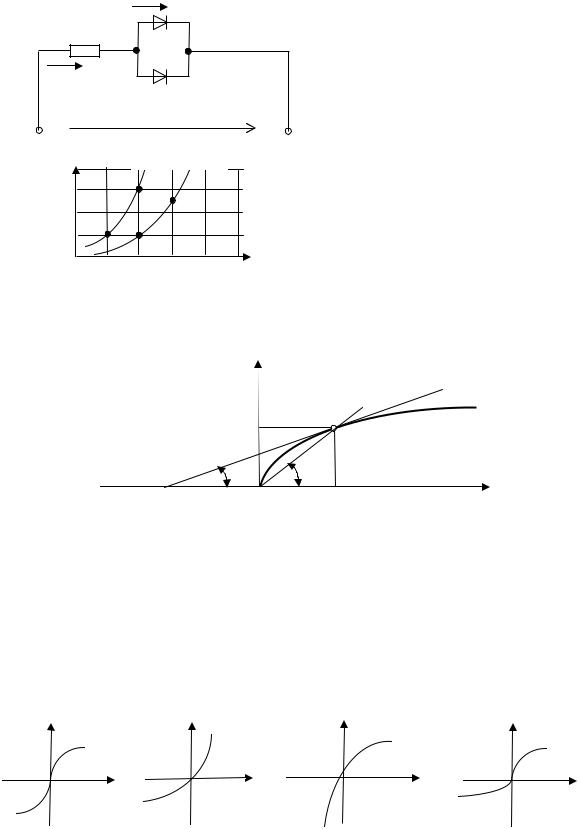
4. Симметричная вольт-амперная характеристика нелинейного элемента соответствует рисунку:
I |
|
I |
|
I |
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
U |
U |
|
||
|
U |
U |
|||||
1 |
2 |
3 |
|
4 |
|||
|
|
|
114 |
|
|
|
|
5. При параллельном соединении заданы вольт-амперные характеристики нелинейных сопротивлений. Если ток I2 равен 3 А, то ток I1 составит:
|
|
I |
|
|
|
|
|
|
|
R2 |
|
|
|
|
|
|
|
|
|
|
U, В |
|
R1 |
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
I |
|
|
R1 |
I2 |
|
|
R2 |
20 |
|
|
|
|
|
|
|
|
|
|||||||
1 |
|
|
|
|
|
10 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
0 |
I, А |
|
|
|
|
|
|
|
|
|
|
|
1 2 3 |
||
|
|
|
|
|
|
|
|
|
|
|||
1) 1А; 2) 3А; 3) 4 А; 4) 2А.
6. При последовательном соединении линейного и нелинейного сопротивлений с характеристиками а и б характеристика эквивалентного сопротивления пройдет:
U2 |
U1 |
|
а |
б |
||
|
|
|
U, В |
|
|
|
|
|
|
30 |
|
|
|
|
I |
20 |
|
|
|
|
|
U |
10 |
|
|
|
|
|
0 |
|
|
|
||
|
|
|
|
I, А |
||
|
|
1 2 |
3 |
|
||
1)выше характеристики а;
2)ниже характеристики б;
3)между ними;
4)для ответа недостаточно данных.
7. Динамическое сопротивление отрицательно на одном из участков характеристики, соответствующей рисунку:
U U U U
I I  I I
I I
1 |
2 |
3 |
|
4 |
|
|
|
|
|
115
8. Триггерным эффектом обладает нелинейный элемент, описываемый характеристикой, соответствующей рисунку:
U |
U |
|
U |
U |
|
I |
I |
I |
I |
1 2 3 4
9. Диоды D1 и D2 имеют ВАХ, изображенные на рисунке. Ток в неразветвленной части цепи I=2 А, падение напряжение на диоде D1 U1=1 В. Тогда сопротивление резистора R будет равно:
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
U1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
D1 |
|
|
|
|
|
|
|
D2 |
|
|
1) 0,25 Ом; |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
U |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
– |
|
2) 1,5 Ом; |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
D2 |
|
|
|
D1 |
|
|
|
3) 1 Ом; |
|||||||
I, А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4) 0,75 Ом. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0,5 1 |
|
|
|
|
1,5 2 U, В |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
10.Если при токе I=5,25 А напряжение на нелинейном элементе U=105 В, а при возрастании тока на ∆I=0,5 А напряжение будет равно 115 В, то дифференциальное сопротивление элемента составит:
1) 10 Ом; 2) 30 Ом; 3) 20 Ом; 4) 100 Ом.
11.Какие из перечисленных элементов являются нелинейными: 1) конденсатор; 2) стабилитрон;
3) катушка без сердечника;
4) катушка с ферромагнитным сердечником;
5) транзистор?
116
5.МАГНИТНЫЕ ЦЕПИ
5.1.Магнитное поле и его параметры
Магнитное поле существует вокруг всякого проводника с током, независимо от материала проводника и характера его проводимости. Источники и приемники электрической энергии представляют собой в общем случае сложные электромагнитные устройства, разнообразные по назначению, принципу действия и конструкции. Их работа основана на использовании магнитного поля. О наличии магнитного поля судят по воздействию, которое оно оказывает на помещенные в него тела. Различают индукционное и электромеханическое (силовое) действия магнитного поля.
Индукционное действие магнитного поля состоит в том, что в проводнике, помещенном в переменное магнитное поле, наводится ЭДС. Если магнитное поле постоянное, то ЭДС в проводнике будет наводиться при перемещении проводника в магнитном поле. На индукционном действии магнитного поля основана работа электрических генераторов, трансформаторов, электроизмерительных приборов и т.д.
Электромеханическое, или силовое, действие магнитного поля заключается в том, что помещенные в поле проводник с током или ферромагнитное тело испытывают действие силы со стороны этого поля. На силовом действии магнитного поля основана работа электрических двигателей, электромагнитных муфт, реле, тяговых устройств и др.
Магнитное поле, необходимое для работы электромагнитного устройства, создается в его магнитной системе с помощью возбудителя (катушки с током или постоянного магнита) и локализуется в заданном объеме за счет применения магнитопровода из ферромагнитного материала.
Величина, характеризующая магнитные свойства среды, т.е. способность намагничиваться, называется магнитной проницаемостью среды.
Широкое использование ферромагнитных материалов во всех электромагнитных устройствах связано с тем, что магнитная проницаемость этих материалов во много раз выше магнитной проницаемости воздуха, что позволяет усилить магнитное поле в заданном рабочем объеме.
117
Абсолютная магнитная проницаемость вакуума является величиной постоянной и называется магнитной постоянной
µ0 = 4π 10−7 ≈125 10−8 . |
(5.1) |
||
Магнитная постоянная имеет размерность |
Гн |
. |
|
|
|
||
|
м |
|
|
Абсолютная магнитная проницаемость любой среды |
|||
µа = µ0 µr , |
(5.2) |
||
где µr – относительная магнитная проницаемость среды. |
|||
В зависимости от магнитной проницаемости µr |
все вещества де- |
||
лятся на диамагнитные, парамагнитные и ферромагнитные. Для большинства материалов относительная магнитная проницаемость µr по-
стоянна и близка к единице. Для ферромагнитных материалов µr яв-
ляется функцией тока, создающего магнитное поле, и достигает больших значений (102–105).
Магнитная индукция В – векторная величина, характеризующая магнитное поле и определяющая силу, действующую на движущуюся заряженную частицу со стороны магнитного поля. В системе СИ магнитная индукция измеряется в теслах (Тл).
Магнитное поле называется однородным, если векторы магнитной индукции В во всех его точках одинаковы.
Напряженность магнитного поля Н – векторная величина, которая не зависит от свойств среды и определяется только токами в проводниках, создающими магнитное поле. Напряженность связана с магнитной индукцией
или |
В = µа Н |
|
|
|
(5.3) |
||||
В = µ0 µr Н , |
|
|
|
(5.4) |
|||||
|
|
|
|
|
|
||||
|
В |
откуда |
|
В |
|
|
|||
|
|
|
Н = |
|
. |
(5.5) |
|||
|
|
|
|
|
|
||||
|
|
|
µ0 |
|
|||||
|
|
|
|
|
|
µr |
|
||
|
|
|
В системе СИ напряженность имеет |
||||||
|
|
|
|
А |
|
|
|
|
|
|
S |
|
размерность |
|
|
|
|
||
|
|
|
. |
|
|
|
|
||
|
|
|
м |
|
|
|
|
||
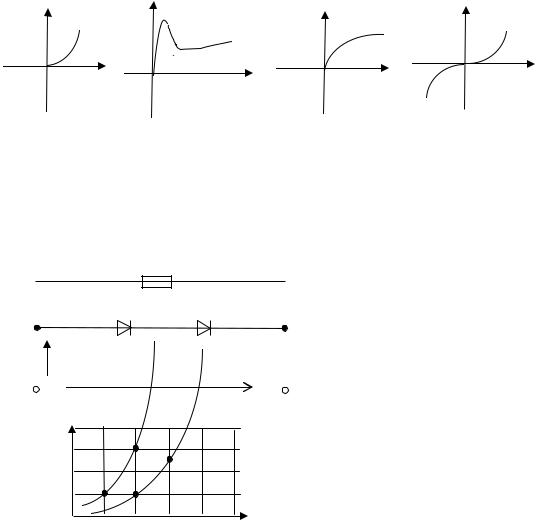
Рис. 5.1. Однородное |
|
|
|
|
|||||
Магнитный поток Ф – это поток маг- |
|||||||||
магнитное поле |
нитной индукции. На рис. 5.1 |
показано |
|||||||
|
|
|
|||||||
однородное магнитное поле, пересекающее плоскость площадью S. Произведение магнитной индукции В однородного магнитного поля
118
на величину площади S, перпендикулярной вектору индукции, называется магнитным потоком Ф.
Ф=В·S. |
(5.6) |
В системе СИ магнитный поток измеряется в веберах (Вб), площадь поперечного сечения – в квадратных метрах (м2).
5.2. Закон полного тока
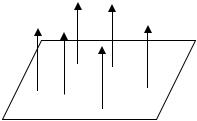
Если какую-либо площадь, пронизываемую несколькими токами, ограничить замкнутым контуром (рис. 5.2), то сумма произведений элементов длины этого контура dℓ и продольных составляющих векторов напряженности НI в каждой точке этого контура, взятая по всему контуру, называется магнитным напряжением Uм или намагничивающей силой F, которая в системе СИ измеряется в амперах (А).
U м = ∫НI dl = F . |
|
(5.7) |
I2 |
dℓ |
|
I4 |
|
|
I1 |
α |
H |
|
||
I3 |
H1 |
|
|
|
Рис. 5.2. К определению магнитного напряжения
Магнитную цепь большинства электротехнических устройств можно представить состоящей из совокупности участков, в пределах каждого из которых можно считать магнитное поле однородным, т.е. с постоянной напряженностью, равной напряженности магнитного поля Hк вдоль средней линии участка длиной ℓк. Для таких магнитных цепей можно заменить интегрирование суммированием.
Если при этом магнитное поле возбуждается катушкой с током I, у которой w витков, то для контура магнитной цепи, сцепленного с витками и состоящего из n участков, можно записать
n
∑H к lк = I w. (5.8)
к=1
Произведение Нк·ℓк=Uмк является магнитным напряжением участка магнитной цепи.
119
