2261

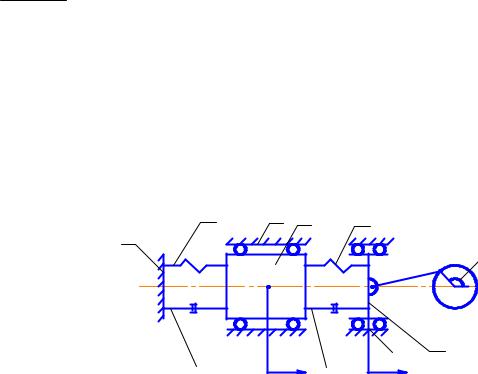
Особенностью этой АЧХ является то, что резонанс наступает при частоте вынужденных колебаний рез , большей, чем частота

собственных колебаний 0. Амплитуда вынужденных колебаний при увеличении частоты вращения дебаланса стремится к значению

m0R . m1 m0

1.10.3. Вынужденные колебания диссипативной системы с кинематическим возбуждением колебаний

На рис. 18 представлена расчётная схема с кинематическим возбуждением колебаний.

Рис. 18. Колебательная система с кинематическим возбуждением

Поводок 8 совершает возвратно-поступательное движение под действием кривошипно-шатунного механизма:

где Rk радиус кривошипа.

Дифференциальное уравнение движения тела 1 можно записать в виде:

mx b1 x b2 (x z ) c1 x c2 (x z) 0, (75)

- 40 -

где x – координата тела 1, отсчитываемая от его среднего положения; z – координата поводка.

Уравнение (75) с учётом равенства (74) можно привести к виду

0 arctgb2 . c2

Сравнивая уравнения (59) и (76) можно заметить, что они отличаются только наличием начальной фазы колебания вынуждающей силы в уравнении (76).

Таким образом, дифференциальное уравнение колебаний при кинематическом возбуждении (76) сводится к такому же виду, как при силовом возбуждении (59), за исключением того, что начальная фаза вынуждающего воздействия при кинематическом возбуждении не равна нулю.

1.10.4. Вынужденные колебания диссипативной системы с принудительным приводом инерционного элемента

Рассмотренные выше системы, совершающие вынужденные колебания являются динамическими. Их движение зависит от сил, действующих на инерционный элемент и от начальных условий. Число степеней свободы динамической системы больше нуля.

Рис. 19. Колебательная система с жёстким приводом

- 41 -

На рис. 19 изображена колебательная система, амплитуда колебаний которой зависит не от частоты возбуждающего воздействия, а от длины кривошипа.

Перемещение такой системы однозначно определяется положением кривошипа, число степеней свободы такой системы равно нулю.

Если длина кривошипа во много раз меньше длины шатуна, то тело 1, совершает гармонические колебания:

где Rk радиус кривошипа.

Согласно принципу Даламбера, сумма всех сил, действующих на тело 1, включая силы инерции, равна нулю.

Принимая S=0 при x=0, получим:

Подставляя выражение (77) в решение дифференциального уравнения (61), получим выражение для амплитуды возмущающей силы:

Как следует из этого уравнения, амплитуда усилия в штоке 5 изменяется с изменением частоты возмущающих колебаний, радиуса кривошипа Rk и массы тела m. На амплитуду усилия в штоке влияют

- 42 -

также коэффициент затухания h и собственная угловая частота системы 0.

Исследовав выражение (81) на минимум можно найти резонансную частоту возмущающей силы

при которой амплитуда усилия в штоке достигает минимума.

При отсутствии диссипативных сопротивлений h=0, и 0 , амплитуда усилия на штоке равна нулю Hрез 0.

На рис. 20 приведены амплитудно-частотные характеристики (АЧХ) амплитуды усилия в штоке в зависимости от угловой частоты вращения кривошипа (угловой частоты возмущающих воздействий).

Рис. 20. Амплитудно-частотная характеристика системы с жёстким приводом

Из АЧХ, приведённых на рис. 20, можно заметить, что при не-

высоких значения коэффициента затухания h 0 амплитуда усилия

2

- 43 -

на штоке H уменьшается с ростом частоты возмущающего воздействия и, достигнув минимума Hрез (при рез ), начинает увеличиваться при дальнейшем увеличении частоты возмущающего воздействия .

Таким образом, резонанс в данной системе проявляет себя снижением усилия в приводе.

При частоте возмущающего воздействия близкой к нулю ам-

плитуда усилия на штоке H равна значению m Rk 02. При отсутствии диссипативных сил (h=0), при приближении частоты возмущающего воздействия к собственной частоте колебаний системы 0

( ) амплитуда усилия на штоке H стремится к нулю.

0

При высоких значениях коэффициента затухания h 0 ам-

2

плитуда усилия на штоке H плавно возрастает с ростом частоты возмущающего воздействия.

1.11. Типы вибровозбудителей

Вибровозбудителями называются устройства, предназначенные для возбуждения механических колебаний. Для возбуждения механических колебаний используются следующие способы возбуждения вибрации.

1. Использование свободных колебаний механической системы. В динамических системах с достаточно малым демпфированием могут использоваться затухающие свободные колебания, энергия которых пополняется периодическими импульсами, сообщаемыми колебательной системе через целое число циклов свободных колебаний. На рис. 21 изображена осциллограмма затухающих колебаний x, энергия которых периодически пополняется импульсами I. На этом же рисунке показана траектория состояний x и x в процессе этих ко-

лебаний.

2. Кинематическое возбуждение колебаний – жёсткий привод с принудительным движением рабочего органа. В таких системах колебания чаще всего создаются кривошипно-шатунными, эксцентриковыми, кулачковыми и др. механизмами. Количество степеней свободы таких систем равно нулю, параметры колебаний (амплитуда, скорость) зависят только от характеристик привода.

- 44 -

Рис. 21. Осциллограмма затухающих колебаний

спополнением энергии

3.Динамическое возбуждение колебаний, осуществляемое внешними силами или моментами, приложенными к инерционным элементам динамической системы. При этом динамическая система должна иметь хотя бы одну степень свободы.

4.Параметрическое возбуждение колебаний системы, осуществляемое путём изменения её параметров – положения центров масс, моментов инерции, коэффициентов жёсткости и т.д.

5.Самовозбуждение колебаний (автоколебания), которые могут возникать в динамических системах за счёт положительных обратных связей между входными и выходными параметрами. Автоколебательные системы обычно содержат усилительные звенья, энергия которых пополняется из внешних источников электрической, гидравлической или пневматической энергии.

По принципу действия и конструктивному исполнению различают достаточно большое количество типов и разновидностей вибровозбудителей – устройств, предназначенных для возбуждения механических колебаний. Выделим из них четыре основные группы:

-45 -

1.Механические преобразователи вращательного движения в колебательное.

2.Гидравлические и пневматические вибрационные устройст-

ва.

3.Электромеханические преобразователи, в которых электрическая энергия преобразуется в энергию механических колебаний.

4.Инерционные вибровозбудители, вынуждающая сила которых вызывается колебательным или вращательным движением инерционных элементов.

К числу механических преобразователей вращательного движения в колебательное относятся кривошипно-шатунные, эксцентриковые, кулачковые механизмы.

К числу гидравлических и пневматических вибрационных устройств относятся поршневые, диафрагменные, сильфонные вибровозбудители, свистки, гудки, сирены, язычковые автоколебательные устройства.

К числу электромеханических преобразователей относятся пьезоэлектрические, магнитострикционные, электродинамические, электромагнитные.

1.12.Центробежные вибровозбудители

Центробежные вибровозбудители – это вибровозбудители с вращательным движением инерционного элемента.

Центробежные вибровозбудители подразделяют на дебалансные и планетарные. Дебалансный вибровозбудитель содержит несбалансированный ротор, называемый дебалансом, вал которого вращается в подшипниках, закреплённых в корпусе. Центробежная вынуждающая сила от вращения дебаласа воспринимается корпусом через подшипники. Вал вращается двигателем, находящимся вне корпуса или встроенным в корпус.

Планетарный вибровозбудитель содержит бегунок, который, обкатываясь по беговой дорожке, передаёт на неё вынуждающую центробежную силу. Достоинством планетарных вибровозбудителей является то, что центробежная сила не нагружает подшипники, а действует непосредственно на корпус, что значительно увеличивает срок службы вибровозбудителя.

- 46 -

Рис. 22. Центробежные вибровозбудители

На рис. 22, а изображён центробежный вибровозбудитель. Позиция 1 – дебаланс; позиция 2 – корпус; 3 – приводной вал.

На рис. 22, б изображён планетарный вибровозбудитель. Позициями обозначены: 1 – бегунок; 2 – поводок; 3 – приводной вал.

Вибровозбудители, изображённые на рис. 22 создают круговую вынуждающую силу, величина которой определяется по формуле:

На рис. 23 схематично изображены некоторые варианты использования центробежных вибровозбудителей.

Рис. 23, а – центробежный вибровозбудитель, создающий круговую (равномерно вращающуюся) вынуждающую силу. Рис. 23, б – комбинация двух вибровозбудителей с дебалансами, вращающимися синхронно, но в противоположном направлении. В результате взаи-

- 47 -

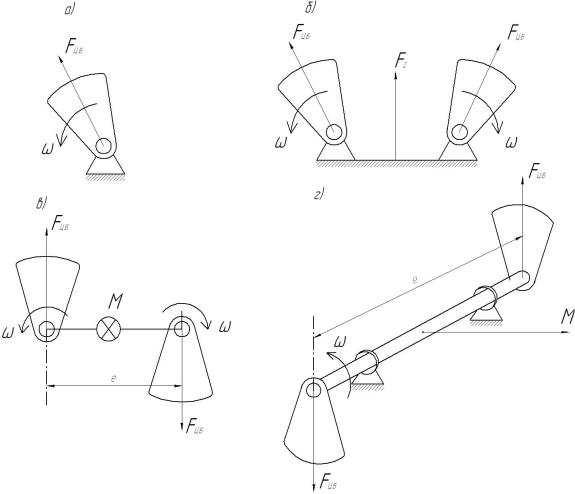
модействия двух вращающихся центробежных сил возникает результирующая сила F , которая постоянно направлена вдоль одной оси.

На рис. 23, в и 23 г изображены схемы центробежных вибровозбудителей, создающих возмущающее воздействие в виде крутящего момента. Величина момента:

При вращении дебалансов в противоположных направлениях (рис 23, в) создаваемый момент постоянен по направлению и изменяется по величине.

При вращении дебалансов в одном направлении (рис. 23, г) вектор создаваемого момента вращается вместе с дебалансами и постоянен по величине.

Рис. 23. Варианты использования центробежных вибровозбудителей

- 48 -

Центробежные вибровозбудители обычно выпускаются со встроенными трёхфазными асинхронными двигателями с короткозамкнутым ротором.

Скорость вращения электродвигателя с короткозамкнутым ротором зависит от частоты питающего напряжения. При частоте f = 50 Гц частота вращения магнитного поля в простейшем асинхронном двигателе, имеющем на статоре три обмотки (А, Б и С) составляет 50 оборотов в секунду или 3000 оборотов в минуту. Эту частоту называют синхронной частотой вращения. Частота вращения ротора асинхронного двигателя всегда несколько меньше за счёт скольжения и при частоте вращения магнитного поля 3000об/мин составляет около 2800об/мин.

Эта частота вращения является максимально возможной для асинхронных двигателей, питающихся от трёхфазной цепи с частотой

50 Гц.

Для увеличения частоты вращения асинхронных двигателей создают специальные источники переменного тока, в которых частота питающего напряжения может увеличиваться до 400 Гц.

Серийно выпускаемые дебалансные вибровозбудители общего назначения имеют частоту 2800 колебаний в минуту, мощность встроенных асинхронных электродвигателей от 0,27 до 1,5 кВт, статический момент массы дебалансов от 2,3 до 34кг см, при этом максимальная вынуждающая сила лежит в пределах от 2000 Н до 30000 Н. Пример расчёта вынуждающей силы.

n 2800об/ мин, 2 n 293рад/ с;

2 85868 1 ;

с2

F m R 2 ,

где m R статический момент массы дебаланса. Если m R 2 кг см 2 10 2 кг м,