2261

угловой скоростью , при этом вектор виброперемещения отстаёт по

фазе от вектора виброскорости на угол 900( ), а от вектора виброу-

2

скорения на угол 1800( ).

1.4. Классификация колебательных систем. Число степеней свободы системы

Классифицировать колебательные системы можно по различным признакам. Одной из важнейших характеристик колебательной системы является число степеней свободы системы – количество независимых числовых параметров, которые однозначно определяют положение системы в любой момент времени.

Число степеней свободы системы прежде всего зависит от степени идеализации системы. Различают системы с конечным и бесконечным числом степеней свободы. Системы, обладающие бесконечным множеством степеней свободы называют распределёнными (континуальными), системы с конечным (ограниченным) числом степеней свободы – дискретными.

Колебания систем с конечным числом степеней свободы описываются обыкновенными дифференциальными уравнениями.

Колебания распределённых систем описываются дифференциальными уравнениями в частных производных.

Колебательные системы можно разделить на линейные и нели-

нейные.

Для линейных систем справедлив принцип суперпозиции, согласно которому сумма откликов системы на воздействия, прилагаемые порознь, равна отклику системы на те же воздействия, прилагаемые совместно.

Для нелинейных систем принцип суперпозиций неприемлем. Линейные колебательные системы описываются дифференци-

альными уравнениями с постоянными коэффициентами. Нелинейные системы описываются дифференциальными уравнениями, в которых коэффициенты при переменных изменяются при изменении значений переменных.

Различают колебательные системы стационарные и нестацио-

нарные.

- 10 -

Свойства нестационарных колебательных систем изменяются с течением времени, свойства стационарных систем принимаются постоянными в течение определённого времени.

Различаютколебательныесистемыавтономныеинеавтономные. Автономные системы – это такие системы, колебательные про-

цессы в которых могут происходить лишь за счёт внутренних источников энергии, а также за счёт энергии, сообщённой системе в виде начального возмущения.

Все прочие системы называются неавтономными. Различие между автономными и неавтономными системами достаточно условно, поскольку граница, отделяющая систему от окружающей среды, выбирается при формированииматематическоймоделиколебательнойсистемы.

Различают колебательные системы консервативные и неконсервативные. Система называется консервативной, если её полная механическая энергия не изменяется в процессе колебаний. В противном случае система называется неконсервативной.

Среди неконсервативных систем можно выделить диссипативные системы – системы, у которых полная механическая энергия рассеивается за счёт действия диссипативных сил (сил трения).

Различают также автоколебательные системы – системы с самовозбуждением колебаний. Автоколебательные системы характеризуются наличием внешнего источника энергии, которая используется для усиления сигнала, а также положительными обратными связями между выходными и входными сигналами.

1.5. Механические системы. Классификация связей механической системы

Механической системой называется множество материальных точек, в котором движение каждой точки зависит от положения и движения остальных точек системы.

Взаимодействие механической системы с окружающей средой определяется внешними возмущающими воздействиями и связями, налагаемыми на систему.

Связями называются условия, которые налагают ограничения на положение точек системы, а также на скорость их перемещения. Если в уравнения связей входят только координаты точек системы и их производные, (связи не изменяются с течением времени), также связи называются стационарными или склерономными.

- 11 -

Если в уравнения связей входит время в явном виде (связи изменяются со временем) такие связи называют нестационарными или

реономными.

Связь называют геометрической, если она накладывает ограничения только на координаты точек системы (в уравнение геометрической связи не входят векторы скоростей). Если связь накладывает ограничения на скорости точек системы, связь называется кинематиче-

ской или дифференциальной.

Связи называются голономными, если они описываются одними уравнениями при работе на растяжение и сжатие, и неголономными – если разными.

Рис. 3. Элементы связей, налагаемых на систему

На рис. 3 схематично изображены некоторые типовые элементы, обычно используемые для описания связей, накладываемых на меха-

нические системы: a) упругий элемент; б) элемент вязкого трения; в) элемент сухого трения (Сен-Венана); г) упруго-вязкий элемент (Кельвина-Фохта); д) упруго-вязкий элемент с остаточной деформацией; е) упруго-вязкий элемент с элементом сухого трения.

Связь называется идеальной, если работа её реакции на всех возможных перемещениях равна нулю (отсутствуют потери энергии).

1.6. Дифференциальные уравнения свободных колебаний механической системы без учёта трения. Период колебаний.

Понятие о линейной и угловой частотах колебаний

Рассмотрим процесс колебаний одномассовой динамической системы с одной степенью свободы, без учёта сил трения. На рис. 4 изображена схема одномассовой динамической системы с упругим элементом.

- 12 -

4

Рис. 4. Схема одномассовой динамической системы: 1 – твёрдое тело с постоянной массой m;

2 – невесомый упругий элемент с коэффициентом жёсткости С;

3 – неподвижная стойка; 4 – направляющие

Ось Х направлена слева направо, параллельно направляющим, в положении равновесия проекция центра тяжести твёрдого тела 1 на ось Х совпадает с началом координат оси Х.

Составим математическую модель колебаний этой динамической системы, приняв следующие допущения: коэффициент жёсткости упругого элемента С постоянен; диссипативные силы (силы трения) отсутствуют; внешние возмущения отсутствуют, действуют только внутренние силы.

В соответствии со вторым законом Ньютона мы можем напи-

сать

где х ускорение тела 1; S сила, с которой пружина 2 действует на тело 1.

Сила сжатия пружины S пропорциональна деформации пружины и направлена в сторону противоположную деформации.

где х смещение твёрдого тела 1 от положения равновесия. Подставляя уравнение (12) в уравнение (11) получим:

Уравнение (15) представляет собой линейное дифференциальное уравнение второго порядка, которое, как известно из курса математики [3], имеет решение в виде общего интеграла:

где c1 и с2 постоянные интегрирования, которые находятся из на-

чальное перемещение (отклонение) и начальная скорость в момент времени t 0.

(16) и (17) найдём выражения для постоянных интегрирования c1 и

с2:

Подставив полученные выражения для постоянных интегрирования в уравнение (16), получим:

- 14 -

Уравнение (19) является решением дифференциального уравнения (15). Решение этого дифференциального уравнения можно записать и в другом виде [3]:

Сравнивая уравнения (15) и (20) можно сделать следующие выводы.

При наличии начального отклонения x0 или начальной скорости

х0 система , изображённая на рис. 4 будет совершать незатухающие гармонические колебания с амплитудой А, начальной фазой 0 и угловой частотой 0.

Эти колебания называются свободными или собственными колебаниями.

Параметры этих колебаний определяются только соотношением величин m и С (массы тела и жёсткости пружины): угловая частота

Из уравнения (20) следует, что начальные условия ( начальное отклонение и начальная скорость) определяют значение амплитуды

- 15 -

колебаний А и начальную фазу колебаний 0 , но не влияют на период колебаний, линейную и угловую частоты колебаний.

Из уравнения (20) следует также, что амплитуда колебаний не влияет на частоту и период колебаний.

Т.е. колебания с большей амплитудой имеют такую же частоту и период, как колебания с меньшей амплитудой при прочих равных условиях.

Колебания, частота которых не зависит от амплитуды, называ-

ются изохронными.

Колебательную систему, описываемую уравнениями (13), (15) и (20) можно назвать консервативной, поскольку диссипативные силы отсутствуют, энергия колебаний не рассеивается, колебания являются незатухающими, продолжаются сколь угодно долго.

Рассмотрим случай, часто встречающийся на практике, когда на упругий элемент действует постоянная сила, обусловленная, например, весом подпружиненной массы.

c

0 ц.т.

т

x mg

Рис. 5. Расчетная схема при действии на тело постоянной силы

На рис. 5 изображена расчётная схема рассматриваемой динамической системы.

Уравнение равновесия системы запишем в виде:

где xcт статическая деформация пружины под действием веса тела mg.

Уравнение движения системы можно записать в виде:

C учётом уравнения (21) можно записать:

m x cx 0.

Поскольку полученное уравнение полностью совпадает с уравнением (13) можно сделать следующий вывод.

Начальная деформация упругого элемента xcт , вызванная действием постоянных внешних сил (например, весом подрессоренной массы) не влияет на характер колебаний системы около положения равновесия. Изменяется только положение равновесия на величину начальной деформации упругого элемента.

Покажем, как, зная только величину статической деформации, можно определить такие характеристики как период, линейную и угловую частоты колебаний.

Из уравнения (21) можно определить значение коэффициента жёсткости упругого элемента.

Подставляя выражение (23) в формулы для определения угловой

илинейной частоты, периода колебаний получим:

-17 -

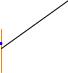
l sin плечо силы веса маятника относительно оси поворота

На рис. 6 изображена расчётная схема колебаний физического маятника. Маятник в процессе колебаний вращается относительно оси качания О, поэтому уравнение движения маятника является уравнением вращательного движения.

где I момент инерции маятника относительно оси качания, угол отклонения маятника от вертикали, l расстояние от оси подвеса до центра тяжести, m масса маятника Уравнение (24) является нелинейным, однако, для малых углов справедливо соотноше-

ние sin .

Уравнение (24) приобретает вид:

I mg l 0. (25)

Разделив обе части уравнения на I , получим:

- 19 -