2261

У математического маятника вся масса сосредоточена в одной точке – центре тяжести. Поэтому момент инерции математического маятника легко вычислить:

Подставляя выражение (29) в уравнения (26), (27), (28), получим для математического маятника:

1.8. Уравнение свободных колебаний линейной диссипативной системы

Диссипативная система – это неконсервативная система, у которой полная механическая энергия при любом движении убывает.

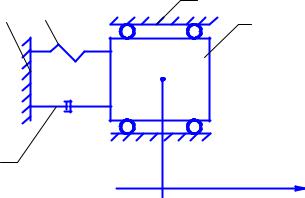
На рис. 7 изображена расчётная схема линейной диссипативной системы с одной степенью свободы. Система не подвергается внешним воздействиям. Поэтому её колебания называют свободными.

Перемещения тела вдоль оси Х отсчитываем от его устойчивого равновесного положения. При движении тела на него действует сила

упругости С с х, и сила вязкого трения В в х .

- 20 -

В уравнении (35) коэффициент h b называется коэффици-

2m

ентом затухания или коэффициентом демпфирования. Коэффициент

0 собственная угловая частота колебаний рад/ с,

Определим размерность коэффициента затухания h и сравним её

сразмерностью 0.

Вуравнении (33) каждое слагаемое имеет размерность силы (Н),

м

а в уравнении (35) – размерность ускорения .

с2

Отсюда следует, что

h b ;

2 m

b x H кг м;

с2

Зная размерность коэффициента вязкого трения b, находим размерность коэффициента затухания h:

кг

Сравнивая размерности собственной угловой частоты колебаний 0 и коэффициента затухания h, мы можем сказать, что эти раз-

ные физические величины имеют одинаковую размерность 1. По-

с

этому мы можем сравнивать эти две величины, вычитать и складывать.

Общий интеграл уравнения (35) имеет различный вид в зависимости от соотношений h и 0.

- 22 -

Другая форма решения дифференциального уравнения (35) имеет вид:

где А – начальная амплитуда колебания;

0 начальная фаза колебания.

Обе формы решения дифференциального уравнения описывают затухающие колебания с постепенно убывающей амплитудой (рис. 8).

- 23 -

Огибающие кривой процесса затухания определяются функция-

ми:

А А0 е ht ,

где A0 начальная ордината огибающей.

Угловая частота свободных затухающих колебаний определяется выражением:

Чаще всего влияние трения на частоту затухающих колебаний пренебрежимо мало, в формуле (38) можно принять h 0.

Таким образом, для практических расчётов можно принять, что угловая частота затухающих колебаний приблизительно равна угловой частоте свободных колебаний системы без трения. Т.е. можно

принять 0 и Т Т0.

- 24 -

- 25 -

На рис. 9 изображён график затухающих колебаний, на котором обозначены амплитуды затухающих колебаний и длительности одного цикла колебаний при докритическом демпфировании.

При закритическом демпфировании коэффициент вязкого трения увеличивается, становятся справедливыми неравенства

В этом случае общее решение дифференциального уравнения движения системы

mx bx cx 0

запишется в виде:

Постоянные интегрирования определяются через начальные условия выражениями:

С1 s2 x0 x0 ;

s1 s2

C2 s1 x0 x0 . s2 s1

Движение, описываемое выражением (46) является апериодиче-

ским (неколебательным). При любых начальных условиях x0 и x0 переменная X асимптотически стремится к нулю.

- 26 -

Рис. 10. Графики апериодических колебаний системы

при различных начальных условиях

Решение дифференциального уравнения (33) в этом случае имеет вид:

Это решение по характеру не отличается от решений, проиллюстрированных на рис. 10.

Таким образом, это движение также носит апериодический (неколебательный) характер.

Вывод: свободное движение диссипативной системы является колебательным при h 0 (коэффициент затухания меньше собственной угловой частоты), и апериодическим (неколебательным) при h 0 .

1.9.Вынужденные колебания системы

содной степенью свободы при отсутствии трения

Уравнение свободных колебаний с учётом трения имеет вид:

mx bx cx 0.

Уравнение свободных колебаний без учёта трения (при b 0):

- 27 -

mx cx 0.

Уравнение вынужденных колебаний отличается от уравнения свободных колебаний тем, что появляется правая часть дифференциального уравнения, которая описывает внешние возмущающие воздействия, действующие на систему (вынуждающую силу). Если вынуждающая сила описывается функцией F H sin t, то уравнение вынужденных колебаний системы с одной степенью свободы при отсутствии трения принимает вид:

Разделим обе части уравнения (48) на массу (коэффициент при x ).

В уравнении (50) 0 собственная угловая частота, угловая частота вынуждающей силы, H – амплитуда вынуждающей силы. Решение этого дифференциального уравнения при 0 и нулевых

начальных условиях (x0 0, x0 0) имеет вид:

Полученное решение представляет разность двух гармонических колебаний с различными частотами ( и 0 ). В действительности этот процесс можно наблюдать лишь в самом начале, т.к. колебания с собственной частотой 0 постепенно затухают.

- 28 -

Таким образом, наиболее существенная стационарная часть процесса (установившиеся вынужденные колебания) описываются выражением:

Амплитуда этих колебаний, происходящих с частотой , определяется уравнением:

В выражении (54) H – это амплитуда возмущающей силы, а ве-

личина с m 2 называется эффективной жёсткостью системы при

гармоническом возбуждении колебаний.

Таким образом, амплитуда вынужденных колебаний равна амплитуде возмущающей силы, деленной на эффективную жёсткость системы.

под действием статически приложенной силы Н.

Разделим числитель и знаменатель выражения (54) на жёсткость С.

- 29 -