
2261
.pdf



 ______________________________
______________________________
Федеральное агентство по образованию ГОУ ВПО «Сибирская государственная автомобильно-дорожная
академия (СибАДИ)»
В.А. Палеев
ОСНОВЫ РАСЧЁТА ВИБРАЦИОННОЙ ТЕХНИКИ
В СТРОИТЕЛЬНЫХ И ДОРОЖНЫХ МАШИНАХ
Учебное пособие
Допущено УМО вузов РФ по образованию в области транспортных машин и транспортно-технологических комплексов в качестве учебного пособия для студентов вузов,
обучающихся по специальности «Подъемно-транспортные, строительные, дорожные машины и оборудование» направления подготовки «Транспортные машины
и транспортно-технологические комплексы»
Омск
СибАДИ
2009
УДК 621.929.7:625.76.08 ББК 30.605.3:39.311-06-05
П 14
Рецензенты:
д-р техн. наук, проф. Н.С. Галдин (СибАДИ); д-р техн. наук, проф. А.Н. Кабаков (ОмГТУ); д-р техн. наук, проф. В.Н.Сорокин (ОмГТУ)
Работа одобрена редакционно-издательским советом академии в качестве учебного пособия для студентов очной и заочной форм обучения специально-
стей 190603 и 190205.
Палеев В.А.
П 14 Основы расчёта вибрационной техники в строительных и дорожных машинах: учебное пособие. – Омск: СибАДИ. 2009. – 108 с.
ISBN 978-5-93204-428-5
Учебное пособие представляет собой краткий курс лекций и контрольные материалы для студентов очной и заочной форм обучения специальностей 190205 и 190603. Контрольные материалы включают варианты индивидуальных заданий для выполнения работ, задачи для практических занятий с примерами решения и тесты для самопроверки.
Табл. 7. Ил. 53. Библиогр.: 8 назв.
ISBN 978-5-93204-428-5
© ГОУ «СибАДИ», 2009

ВВЕДЕНИЕ
Настоящее учебное пособие предназначено для студентов, получающих подготовку по специальности 170900 (190205.65) – «Подъём- но-транспортные, строительные, дорожные машины и оборудование» направления подготовки 653200 (190200.65) – «Транспортные машины и транспортно-технологические комплексы», а также специализации 170919 – Подъёмно-транспортные и специальные машины для соору-
жения и ремонта нефте- и газопроводов, для очной, заочной и дистан-
ционной форм обучения.
В первой части учебного пособия изложены основы теории и расчёта вибрационной техники, даны конструктивные схемы основных типов вибрационных механизмов, применяемых в строительных и дорожных машинах.
Вторая часть посвящена примерам решения типовых задач, а также примерам выполнения контрольных работ для студентов заочной и дистанционной форм обучения.
Данное учебное пособие может быть использовано при изучении курсов «Теория колебаний и вибрационная техника», «Вибрационная техника», при выполнении контрольных работ, курсовых и дипломных проектов студентами механических специальностей автомобильнодорожных вузов.
Автор выражает глубокую благодарность профессору Н.С. Галдину, профессору А.И. Демиденко, ведущему доценту В.И. Лиошенко за ценные советы и замечания, высказанные при подготовке рукописи к изданию, а также сотрудникам и студентам СибАДИ, оказавшим содействие и помощь в издании данного учебного пособия.
- 3 -

Часть 1. ЛЕКЦИОННЫЙ КУРС
1.1. Классификация колебательных процессов. Механические колебания.
Виды вибрационной техники
1.1.1. Виды колебательных процессов
Различают следующие виды колебательных процессов:
Свободные колебания (собственные) – это колебания, которые совершаются при отсутствии внешних возмущающих воздействий, без поступления энергии от внешних источников.
Свободные колебания совершаются за счет энергии, которая сообщается системе, либо в виде начального перемещения упругих элементов, либо в виде начальной скорости характерных точек системы в некоторый начальный момент времени.
Вынужденные колебания – это колебания, которые совершаются при наличии внешних возмущающих воздействий, за счёт энергии этих возмущающих воздействий.
Параметрические колебания – это колебания, вызываемые из-
менением во времени параметров системы (например, изменение положения центра тяжести).
Автоколебания – это самовозбуждающиеся колебания, которые обычно возникают в системах усиления сигналов с положительной обратной связью между входными и выходными сигналами.
В качестве примера автоколебаний можно назвать “свист”, который возникает в усилителях звуковой частоты при появлении акустической обратной связи между динамиками (выходной сигнал) и микрофоном (входной сигнал).
- 4 -
В колебательных системах возможны также процессы смешанного характера, которые могут возникать в результате наложения одних колебаний на другие. Например, в результате наложения собственных и вынужденных колебаний системы.
1.1.2. Механические колебания
Колебательные перемещения физических тел или геометриче-
ских фигур называют механическими колебаниями или вибрацией.
Используя термин ”вибрация” мы всегда подразумеваем механические колебания.
В то же время к механическим колебаниям относятся не только колебания параметров движения (перемещение, скорость, ускорение), но и колебания иных механических величин (масса, сила, давление и т.д.). Поэтому термин “механические колебания” является более широким, чем термин “вибрация”.
Вибрацию можно рассматривать как разновидность механических колебаний.
1.1.3. Виды вибрационной техники
Различают следующие виды вибрационной техники:
а) машины, устройства, инструменты в которых преднамеренно возбуждается вибрация для выполнения полезных функций;
б) аппаратура и устройства для контроля и измерения вибрации; в) аппаратура и устройства для предотвращения, подавления,
гашения, изоляции вредной вибрации.
Необходимо отметить, что длительные воздействия вибрации на организм человека вызывает заболевание, называемое “виброболезнью’’.
Это заболевание поражает в первую очередь кости и суставы, вызывает сильные ночные боли, и приводит к полной утрате трудоспособности.
В строительстве применяют следующие основные виды вибрационной техники:
-вибросортировочные машины – для разделения строительных материалов (щебня, песка) на фракции по крупности зёрен;
-вибрационные площадки – для формования железобетонных изделий;
-5 -

-вибрационные машины для уплотнения грунта, дорожных оснований и покрытий (виброкатки, виброплиты, вибротрамбовки);
-вибропогружатели свай и вибромолоты;
-землеройные машины с ударно-вибрационными рабочими органами;
-вибровыгружатели сыпучих грузов из вагонов;
-вибробункеры, виброжолобы, виброконвейеры и т.д.
1.2.Параметры периодических колебаний.
Понятие о гармонических колебаниях
Среди колебательных процессов особый интерес представляют периодические колебания, когда движение полностью повторяется через определённые равные промежутки времени. Такой промежуток времени называется периодом колебаний.
Функция f (t) называется периодической, если существует постоянная величина T, называемая периодом, для которой имеет место равенство
f (t) f (t T) f (t 2T) ...f (t nT), |
(1) |
где n – произвольное целое число. Период колебаний T измеряется в секундах.
Величина обратная периоду колебаний называется линейной частотой.
f |
1 |
, |
(2) |
|
T
линейная частота измеряется в колебаниях в секунду 1c (Герц).
Среди множества периодических колебаний особое место зани-
мают синусоидальные или гармонические колебания:
у А sin( t 0 ), |
(3) |
где A – амплитуда колебаний; угловая |
частота колебаний; |
0 начальная фаза колебаний; t текущее время.
Угловую частоту можно выразить через период колебаний:
- 6 -
|
2 |
. |
(4) |
|
T
В этом случае выражение (3) принимает вид:
у А sin( |
2 |
0 ). |
(5) |
|
|||
|
Т |
|
|
Амплитуда колебаний A это абсолютная величина наибольшего отклонения от среднего положения при гармонических (синусоидальных) колебаниях.
В случае негармонических колебаний говорят о пиковом значении колеблющейся величины или о полуразмахе колебаний.
Размах колебаний – величина, равная удвоенной амплитуде, представляет собой расстояние между крайними противоположными положениями колеблющейся точки.
Для гармонических колебаний термины – амплитуда, пиковое значение, полуразмах колебаний являются синонимами.
Угол ( t 0 ) синусоидальной функции называют фазой ко- |
||||
лебания. |
|
|
|
t |
y |
y |
Т |
Т |
|
A |
x |
A |
R |
|
w f |
|
|
||
Е Е f |
|
|
||
|
Е |
y=A*sin(w+tjЕ) |
|
|
|
x |
|
||
R |
Т |
|
||
|
|
x=A*cos(w+j ) |
|
|
t |
|
|
tЕ |
|
|
|
|
|
|
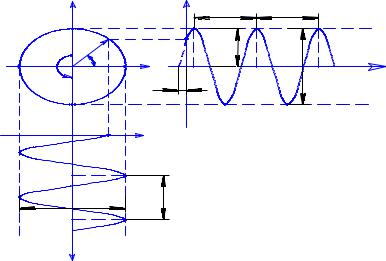
Рис. 1. Вращающийся радиус-вектор |
|
|||
как форма представления колебательного процесса |
||||
Фаза колебания позволяет определить значение колеблющейся величины в любой, произвольный момент времени.
- 7 -
Величина 0 называется начальной фазой колебания и представляет собой фазу колебания в начальный момент времени (при
t0).
Втеории колебаний очень часто колеблющиеся величины представляют в виде радиус-векторов, вращающихся с угловой скоростью .
На рис. 1 изображён вектор А, который вращается с угловой скоростью , из начального положения, определяемого углом 0. Проекции этого вращающегося вектора на вертикальную и горизонтальную оси совершают гармонические колебания:
у А sin( t 0 ); |
(6) |
x А cos( t 0 ). |
(7) |
1.3. Кинематика синусоидальных колебаний. Графики перемещения, скорости, ускорения
Уравнение виброперемещения для гармонических колебаний можно записать в виде:
у А sin( t 0 ). |
(8) |
Дифференцируя это выражение по времени, получим выражение для виброскорости:
у/ А cos( t 0 ).
Пользуясь формулой приведения, известной из тригонометрии cos sin(900 ) можно записать:
у/ А cos( t 0 ) A sin( t 0 900 ). |
(9) |
- 8 -
Из уравнения (9) можно заключить, что амплитуда виброскоро- |
|||||
сти равна A , а колебания виброскорости опережают по фазе коле- |
|||||
бания виброперемещения на угол 900. |
|
|
|||
Продифференцировав по времени выражение для виброскоро- |
|||||
сти, получим выражение для виброускорения (9): |
|
||||
у// |
А 2 |
cos( t 0 |
900 ). |
|
|
C помощью формулы приведения cos sin(900 ) получим: |
|||||
у// |
А 2 |
sin( t 0 |
1800 ). |
(10) |
|
Сравнивая выражения (8), (9), (10) можно заключить, что виб- |
|||||
роускорение опережает по фазе на 900 виброскорость и на 1800 |
виб- |
||||
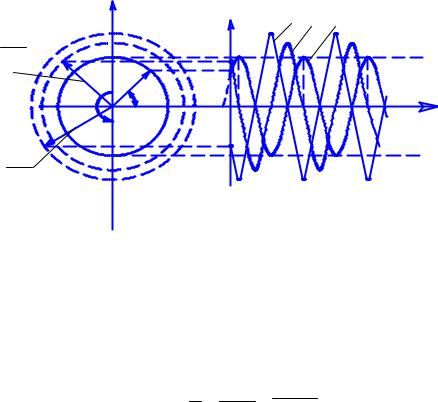
роперемещение. Амплитуда виброускорения равна А 2. На рис. 2 |
|||||
изображены графики виброперемещения у |
f( t ), виброскорости |
||||
y f( t ) и виброускорения y |
f( t ). |
|
|
||
y |
|
y |
y II |
yI y |
|
|
|
|
|
|
|
A*w |
|
|
|
|
|
A |
|
|
|
|
|
w |
|
|
|
|
|
Е |
|
|
|
|
|
2 |
|
|
|
|
|
A*w |
|
|
|
|
|
|
y=A*sin(w+j) |
|
|
||
|
|
|
tЕ |
|
|
|
I |
|
|
Е |
|
|
y=A* |
*sin(w+j+90 ) |
|
||
|
|
|
w tЕ |
|
|
|
I I |
2 |
Е |
|
|
|
y=A* |
|
|||
|
|
|
|||
|
*sin(wj+ +180 ) |
|
|||
|
|
|
w tЕ |
|
|
Рис. 2. Графики виброперемещения, виброскорости и виброускорения |
|
||||
Виброперемещение, виброскорость и виброускорение представ-
лены на рис. 2 в виде векторовA, A , A 2 , которые вращаются с
- 9 -
