
2140
.pdf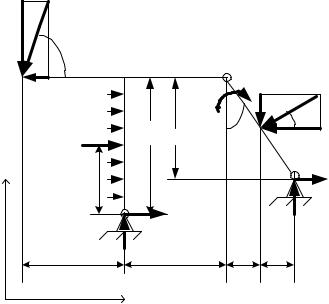
Yi YA Pcos45 Q 0 YA Pcos45 Q 5cos45 2,4
5,94кН.
Курсовая работа С-3
Определение реакций опор составной конструкции (система двух тел)
Конструкция, показанная на рис.79, состоит из двух частей, соединенных цилиндрическим шарниром в точке С. Определить реакции опор и давление в
P1 |
|
|
|
|
|
|
P1y |
|
|
|
|
|
|
600 |
|
|
C |
|
|
|
D |
|
|
|
|
P2y |
P2 |
P1x |
q |
|
M |
|
|
|
|
|
|
||||
|
|
|
|
P |
||
Q |
|
4 |
3 |
|
||
|
|
|
2x |
|||
|
|
|
B |
|||
y |
|
|
|
|
|
|
|
2 |
A |
O |
|
|
XB |
|
|
XA |
|
|
YB |
|
|
|
YA |
|
|
||
3 |
|
3 |
1 |
1 |
|
|
|
|
x |
|
|
|
|
|
|
|
Рис.79 |
|
|
|
соединительном шарнире С. |
|
|
Активные силы, |
приложенные к |
конструкции, имеют значения: |
P1 5кН; P2 7кН; |
|
P1 |
M 22 кН м; |
q 2 кН / м. |
|
Методика выполнения курсовой работы С–3
1.Записать условие задачи и данные Вашего варианта. Выполнить рисунок всей конструкции. На рисунке показать:
активные силы. Распределенную нагрузку заменить сосредоточенной силой Q=q 4 2 4 8кН;
показать соответственно типу связей реакции опор. При этом
72
реакции соединительного шарнира не нужно показывать, так как если вся |
|||||||||
конструкция рассматривается как одно тело, то силы в соединительном |
|||||||||
шарнире относятся к внутренним силам и поэтому взаимно уравновешены. |
|||||||||
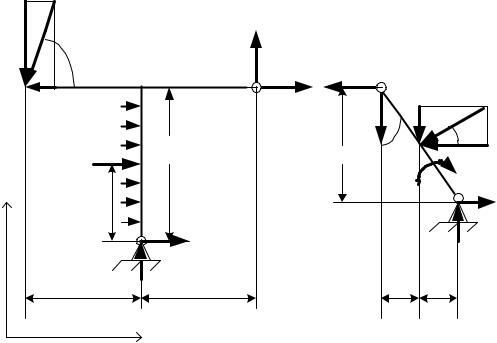
2.«Разбить» конструкцию по шарниру C и выполнить рисунки левой |
|||||||||
и правой частей, как показано на рис.80. |
|
|
|
|
|||||
Выполняя рисунок тела DAC, следует показать и силу, с которой |
|||||||||
на него действует тело CB составляющие |
реакции |
цилиндрического |
|||||||
шарнира C: XC;YC . |
|
|
|
|
|
|
|
|
|
Выполняя рисунок тела CB, покажите силы X1C;Y1C , с которыми на |
|||||||||
него действует тело DAC. |
|
|
|
|
|
|
|
||
P1 |
|
|
|
|
|
|
|
|
|
P1y |
|
YC |
|
|
|
1 |
|
|
|
600 |
|
X |
|
|
|
|
|
||
|
C |
C |
|
XC |
C |
|
|
||
D |
|
|
|
|
|
P2y |
P2 |
||
|
|
|
|
|
|
|
|||
P1x |
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
P |
||
Q |
4 |
|
|
|
|
3 |
YC1 |
||
|
|
|
|
|
2x |
||||
|
|
|
|
|
M |
||||
y |
|
|
|
|
|
|
|
|
B |
|
2 |
|
|
|
|
O |
|
|
XB |
|
A |
XA |
|
|
|
|
|
|
YB |
|
YA |
|
|
|
|
|
|
||
3 |
3 |
|
|
|
|
1 |
1 |
|
|
|
x |
Рис.80 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|||
Следует иметь в виду, что силы X |
C |
и X1 |
являются силами действия |
||||||
|
|
|
|
|
C |
|
|
|
|
и противодействия, поэтому они равны по модулю друг другу и противо- |
|||||||||
положно друг другу направлены. То же самое относится и к силам YC и
YC1 .
3. На всю конструкцию, а также на каждое из тел конструкции действует соответствующая плоская произвольная система сил. Если для одного тела составляется три независимых уравнений равновесия, то для системы, состоящей из двух тел, таких уравнений 6.
Составляя уравнение равновесия, следует делать пояснения,
73

равновесие какого тела рассматривается.
Выбрать направление осей координат и показать оси координат на каждом рисунке.
Силы, не параллельные осям, разложить на составляющие, направленные по осям и записать их значения.
Раскладываем силу P1 P1x P1y. Из рис.80 видно:
P1x P1cos60 5cos60 2,5кН;
P1y P1sin60 5sin60 4,33кН.
Раскладываем силу P2 P2x P2y .
Определим предварительно из треугольника COB:
sin |
|
2 |
|
0,54; |
cos |
|
3 |
|
0,83. |
|
|
|
|
|
|
||||
|
|
22 32 |
|
|
22 32 |
||||
Тогда
P2x P2 cos 7 0,83 5,81кН;
P2y P2sin 7 0,54 3,78кН.
Итак, рассматривая систему уравновешенных сил, приложенных ко всей конструкции, составим уравнение моментов сил относительно полюса
B:
mB P1x 3 P1y 8 Q 1 YA 5 XA 1 M P2x 1,5
(1)
P2y 1 0.
Рассматривая систему уравновешенных сил, приложенных к телу DAC, составим уравнение моментов относительно полюса C:
mC XA 4 YA 3 Q 2 P1y 6 0. |
(2) |
Для этой же системы сил составим уравнение проекций сил на координатные оси:
Xi XC XA Q Px 0; |
(3) |
Yi YC YA P1y 0. |
(4) |
Рассматривая систему уравновешенных сил, приложенных к телуCB, составим уравнение моментов относительно полюса C:
74

m |
M P |
1,52 12 Y |
B |
2 X |
B |
3 0. |
(5) |
C |
2 |
|
|
|
|
Для этой же системы сил составим уравнение проекций:
X X1 |
P |
X |
B |
0. |
(6) |
|
i |
C |
2x |
|
|
|
|
4.Решить систему составленных уравнений следующим образом. Из уравнения (1) выражаем
XA 5YA
M P2x 1,5 P2y 1 P1x 3 P1y 8 Q 1
22 5,811,5 3,78 1 2,5 3 4,33 8 8 1 24,64
XA 5YA 24,64,
подставляем в уравнение (2):
|
mC (5YA 24,64) 4 YA 3 Q 2 P1y 6 0 |
|||||||
Y |
|
|
1 |
(24,64 4 Q 2 P |
6) |
|
1 |
(98,56 8 2 4,33 6) |
|
|
17 |
||||||
|
A |
17 |
1y |
|
|
|||
3,36кН.
Следовательно, XA 5YA 24,64 5 3,36 24,64 7,94кН.
Отрицательное значение указывает, что на рис.79,80 показано неправильное направление этой реакции.
Из уравнения (3) находим
XC XA Q P1x ( 7,94) 8 2,5 2,44кН.
Из уравнения (4) находим
YC YA P1y 3,36 4,33 0,97кН.
Из уравнения (6) находим
XB XC1 P2x 2,44 5,81 8,25 кН.
Из уравнения (5) находим |
|
|
|
|
|
|
||||||
Y |
|
1 |
(M P |
|
X |
|
3) |
1 |
(22 7 |
|
8,25 3) 6,45кН |
|
5 |
B |
5 |
||||||||||
|
|
|||||||||||
B |
2 |
2 |
|
|
2 |
|
|
|
||||
75
Курсовая работа С-7
Определение реакций опор твердого тела
Найти реакции опор конструкции, показанной на рисунке для Вашего варианта.
Примечания:
1.Считать, что в вариантах 16, 18, 22-26 петли не препятствуют перемещению рамы вдоль оси AB.
2.В вариантах 20 и 21 соприкасающиеся поверхности в точке C считать абсолютно гладкими.
3.В вариантах 3 и 28 горизонтально расположенная плита закреплена невесомыми стержнями, которые являются связями.
4.В вариантах 27 и 30 закрепление балки в точке A жесткое, препятствует не только перемещению вдоль осей, но и повороту балки относительно этих осей. Реакция жесткой заделки в задачах пространственной статики
содержит шесть величин:
mx,my,mz реактивные моменты относительно каждой оси;
XA,YA,ZA составляющие реакции жесткой заделки, |
направлен- |
||||||
ные по соответствующей оси. |
|
||||||
|
|
Методика выполнения курсовой работы С–7 |
|
||||
1.Сделать рисунок Вашего варианта задания. Записать условие задачи |
|||||||
|
z |
|
|
|
|
и данные, приведенные в таблице (см. при- |
|
|
|
|
|
|
ложение). |
|
|
450 |
C |
|
P |
r |
|
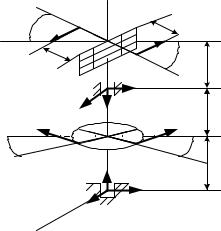
Условие задачи. Составить все |
уравнения |
P |
r |
|
|
|
равновесия конструкции (рис.81) и опреде- |
||
|
D |
45 |
0 |
|
|||
|
|
|
c |
лить опорные реакции, если дано: |
|||
|
B |
G |
YB |
|
|
T 8кН; G 2кН; a 20см; |
b 30см; |
T |
XB |
|
t |
b |
c 40см; R 20см; r 15см. |
||
|
|
|
|||||
450 |
|
|
Y450 |
a |
Известно, что CD Ax, |
T 2t, T |
|
|
ZA |
|
|
A |
|||
|
A |
|
|
y |
иt Az, а также, что сила P параллельна |
||
|
|
|
YA |
|
|||
|
XA |
|
|
оси Ax. |
|
||
x |
|
|
|
При выборе тела, равновесие которого |
|||
|
|
Рис.81 |
|
|
будем рассматривать, следует выбирать всю |
||
|
|
|
|
|
|
конструкцию и рассматривать ее как одно |
|
тело. В нашей задаче это вертикальная ось, диск радиуса R, |
рамка 1 со |
||||||
стержнемCD (рис.81). |
|
|
|
||||
|
|
|
|
|
|
76 |
|
2.Показать силы, действующие на конструкцию. К активным силам |
|||||||||||
относятся все силы, показанные на рис.81. Это силы T и t |
, |
лежащие в |
|||||||||
плоскости диска, т.е. в горизонтальной плоскости, и |
|
R |
|
|
|
|
|
||||
направленные по |
касательной к диску. |
Если |
по- |
|
|
|
|
|
|
|
|
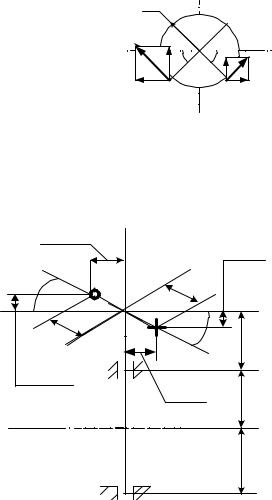
смотреть на диск сверху (со стороны оси Az), то |
|
T |
|
z |
|
|
y |
||||
|
45 |
0 |
45 |
0 |
|||||||
это выглядит так, как показано на рис.82. Для на- |
|
|
|
t |
|
||||||
|
|
|
|
|
|
||||||
глядности силы |
разложены на составляющие |
по |
|
|
|
|
|
|
|
||
осям координат. |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На рассматриваемую |
конструкцию |
действует |
|
|
Рис.82 |
|
|
||||
пара сил. Чтобы правильно вычислить моменты |
|
|
|
|
|
|
|
||||
этой пары сил, на рис.83 показан вид пары сил со стороны оси Ax. Из рис. |
|||||||||||
83 видно, что плечо пары сил относительно оси z равно 2rcos30 , а от- |
|||||||||||
носительно оси y равно 2rcos60 . |
rcos30 |
z |
|
|
|
|
|
|
|||
Это следует иметь в виду при со- |
|
|
|
rcos60 |
|
||||||
|
|
|
|
|
|
|
|||||
ставлении уравнения моментов. |
300 |
C |
|
|
r |
|
|
|
|||
3. На рисунке к заданию (рис.81) |
|
|
|
|
|
||||||
показать реакции опор. |
Учитывая, |
P |
|
|
D |
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
||||
что связь в точке B не препятствует |
|
|
|
P |
300 |
|
c |
|
|||
перемещению рассматриваемого те- |
rcos60 |
B |
|
|
|
|
|
|
|
||
ла по вертикальной оси, реакция |
|
|
rcos30 |
|
|
||||||
опоры лежит в горизонтальной плос- |
|
|
|
|
b |
|
|||||
|
|
|
|
|
|
|
|
||||
кости и ее составляющие: |
XB,YB. |
|
|
|
|
|
|
|
a |
|
|
Связь опоры A |
осуществляет под- |
|
|
|
|
|
|
|
|
||
|
x |
A |
|
|
|
|
|
||||
пятник. Реакция подпятника раскла- |
|
|
|
|
|
y |
|||||
|
|
|
|
|
|
|
|
||||
дывается по трем осям: XA,YA,ZA. |
Рис.83 |
4.Для произвольной пространственной системы сил составляются 6 уравнений равновесия:
Xi T cos45 tcos45 XA XB 0;
Yi T cos450 tcos450 YA YB 0;
Zi G ZA 0;
mx Tcos450a tcos450a YB(a b) 0;
(1)
(2)
(3)
(4)
m |
y |
T cos450a tcos450a P 2rcos600 |
X |
B |
(a b) 0; (5) |
|
|
|
|
||
mz T R t R P 2rcos300 0. |
|
|
(6) |
||
77

5. При выполнении курсовой работы нужно решить систему уравнений относительно неизвестных по условию задачи и выполнить вычисления.
Систему уравнений решаем так
из уравнения (6) вычисляем P |
(T t)R |
|
4 20 |
3,04 кН. |
|
2rcos300 |
215cos300 |
||||
|
|
|
Из уравнения (5) вычисляем
XB (T t)cos45 a P2rcos60 2,94кН. a b
Из уравнения (4) вычисляем
YB (T t)cos45 a 4cos45 20 1,13кН. a b 50
Из уравнения (3) вычисляем ZA G 2кН.
Из уравнения (2) вычисляем YA YB (T t)cos45 1,7кН.
Из уравнения (1) вычисляем
XA XB (T t)cos45 2,94 4cos45 0,11кН.
78
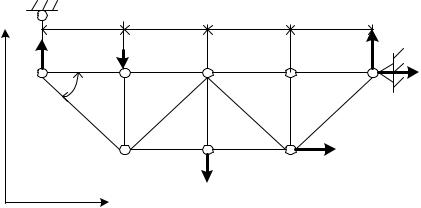
Тема 6
РАСЧЕТ ФЕРМЫ
Фермой называется несущая стержневая геометрически неизменяемая (жесткая) конструкция. Это башни и стрелы подъемных кранов, железнодорожные мосты, мачты электропередач.
В механике рассматривается модель фермы, которая отличается от реальной фермы в связи с допущениями, принятыми при построении расчетной модели фермы.
Приняты следующие допущения:
все стержни фермы лежат в одной плоскости;
стержни фермы жесткие, невесомые (весом стержней пренебрегаем) и соединены между собой шарнирами;
трение в шарнирах не учитываем;
нагрузку прикладываем только в шарнирах, соединяющих стержни (узлах).
Эти допущения дают возможность рассчитать ферму методами статики. Неизбежная при этом в силу принятых допущений ошибка не превышает допустимой точности инженерных расчетов.
На рис.84 показана расчетная модель фермы, выполненная с учетом вышеперечисленных допущений. Стержни фермы обозначаются цифрами: 1–опорный стержень; 2,5,9,13 – стержни верхнего пояса; 7,11 – стержни нижнего пояса; 4,8,12 – стойки; 3,6,10,14 – раскосы.
Буквами обозначены узлы: A,C,E,F,B,K,L,D.
y |
a |
a |
a |
A RA 2 C |
P1 |
5 |
E |
9 |
|
||||
|
|
|
|
|
3 |
4 |
6 |
8 |
10 |
|
|
|||
|
|
7 |
L |
11 |
|
D |
|
|
|
|
|
P2 |
|
|
x |
|
|
|
|
|
|
Рис.84 |
||
|
|
|
||
|
a |
YB |
|
|
|
F |
13 |
XB |
12 |
14 |
B |
K |
P3 |
|
Произведем расчет фермы при следующих данных:
P1 12 кН, P2 8кН, P3 2кН, 45 .
79
Расчет фермы заключается в определении сил, сжимающих или растягивающих каждый стержень. Эти силы называются усилиями.
Начинают расчет с определения опорных реакций.
1. Определение опорных реакций
При определении опорных реакций рассматривается равновесие всей фермы, как одного твердого тела.
Силы, действующие на ферму, на рис.84 показаны. Это активные силы
P1,P2,P3 и реакции связей, наложенных на ферму в точках A (стержень
1) и B(неподвижный шарнир): RA,XB,YB.
Так как эти силы образуют плоскую систему произвольно расположенных сил, то составляем следующие уравнения равновесия:
mB P3 a P2 2a P1 3a RA 4a 0;
Xi XB P3 0;
Yi RA P1 P2 YB 0.
Решая эти уравнения, находим из первого уравнения RA 13,5кН; из второго XB 2кН (отрицательное значение указывает, что в действи-
тельности эта реакция направлена в противоположную сторону, чем показано на рисунке); из третьего YA 6,5кН.
2. Определение усилий в стержнях фермы
Аналитически усилия в стержнях фермы определяется двумя методами. Рассмотрим каждый из этих методов.
2.1. Определение усилий в стержнях фермы методом вырезания узлов
При этом способе рассматривается равновесие каждого узла фермы в отдельности. Так как силы, приложенные к отдельному узлу, образуют плоскую систему сходящихся сил, то независимыми являются только два уравнения равновесия. Поэтому, чтобы количество неизвестных усилий не превышало количества уравнений равновесия, следует вырезать узел, в
котором сходятся не более двух стержней, усилия в которых неизвестны.
80

Делая предположение, что все стержни фермы растянуты, усилия направлять от узла. При расчете усилия стержней, работающих на сжатие, получаются отрицательными.
Рассматриваем равновесие узла A (рис.85)
Показываем на рис.85 силы, приложенные к этому
узлу, направляя усилия 2-го и 3-го стержней (S2,S3) от
узла. Составляем уравнения равновесия:
Xi S2 S3 cos45 0;Yi RA S3 cos45 0.
Решаем систему этих уравнений и находим из 2-го
уравнения S |
3 |
|
RA |
|
13,5 |
19,09 кН. |
cos45 |
|
|||||
|
|
|
cos45 |
|||
y
 RA
RA
A  S2
S2 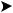 X
X
 S3
S3
Рис.85
Из 1-го уравнения S2 S3 cos45 19,09 cos45 13,5кН.
Рассматриваем равновесие узла C(рис.86).
Силы, приложенные к узлу: активная сила P1
и усилия стержней S2,S4,S5. При этом, несмотря на то, что стержень 2 сжат, усилие этого стержня
S2, во избежание путаницы, направляем от узла.
При решении уравнений значение S2 записываем
с тем знаком, с которым оно было получено при решении предыдущих уравнений (т.е. отрицательным).
Составляем уравнения равновесия:
Находим из уравнений S5 S2 13,5кН;
S4 P1 12кН.
y
P1 |
C S |
|
x |
S2 |
|
5 |
S4
Рис.86
.
81
