
2140
.pdf
3. Две пары сил эквивалентны одной паре, момент которой равен геометрической сумме главных моментов двух приводимых пар, т.е.
M M1 M2.
Таким образом, т.к. действие пары сил на тело полностью характеризуется моментом этой пары, то с целью упрощения терминологии вместо выражения на тело «действует пара сил, момент которой…» будем говорить « на тело действует момент».
Приведение произвольной системы сил к простейшему виду
Любую систему сил в общем случае можно заменить эквивалентной системой, состоящей из одной силы и момента (пары сил.) При этом приведенная сила приложена в выбранном центре приведения и равна главному вектору системы сил. Момент приведенной пары равен главному моменту системы относительно центра приведения.
На рис 56-60 показано, как первоначальная система сил F1F2F3 при-
ведена к полюсу O, (который будем называть центром приведения) следующим образом:
а) на рис.56 показана первоначальная система сил F1F2F3 ,
F1
F2
F3

Рис.56
b) на рис. 57 к первоначальной системе сил присоединены уравновешенные силы
|
|
|
h |
|
|
|
F11,F1, приложенные в цен- |
F1 |
|
|
|
||||
|
F1 |
||||||
|
|
|
|
тре приведения O, |
|||
|
|
|
|
|
|
|
|
F2
F3
 O
O
F11 
Рис.57
52

с) на рис. 58, учитывая, что сила F1 первоначальной системы и сила F11
образуют пару сил, действие пары сил представлено моментом этой пары.
mo(F1) F1
F2  F3
F3
 O
O
Рис.58
d) на рис. 59 точно так же приведены к центру O силы F2 и F3. В ре-
зультате получена система, состоящая из трех сил, приложенных в точке O, и трех пар сил; действие которых учитывают их моменты;
mo(F2) |
|
F1 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
O |
|
|
mo(F1) |
|
|
|
|
|
|
|
|
|
F3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
mo(F3) |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
Рис.59 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||||
е) на рис.60 три приведенные силы сложили |
Mo |
|
F1 |
|||||||||||||
и получили силуR. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Сложив моменты трёх пар, получили |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
R |
|
|
|
|
F2 |
|||||||||
момент Mo; |
|
|
|
|
|
O |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
F3 |
|||||||||
Полученная в результате приведения |
|
|
|
|||||||||||||
система состоит из силы R и момента Mo. |
|
Рис.60 |
||||||||||||||
Эта система и первоначальная система F1F2F3 эквивалентны друг дру- |
||||||||||||||||
гу, т.к. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
R F1 F2 F3; |
|
|
(4.8) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Mo mo(F1) mo(F2) .mo(F3) |
|
(4.9) |
||||||||||||||
|
|
|
53 |
|
|
|
|
|
|
|
|
|
|
|
||

6. Теорема о моменте равнодействующей (теорема Вариньона).
Момент относительно некоторого полюса O равнодействующей
равен сумме моментов относительно этого полюса составляющих сил.
Для доказательства этой теоремы воспользуемся теоремой об эквивалентности двух систем сил (рис.61). Одна из сис-
|
|
|
|
|
|
R |
|
тем состоит из одной силыR, другая включает |
|||||
|
|
|
|
|
|
|
|||||||
Ry |
|
|
|
|
|
|
|
силы Rx,Ry. Эти системы |
эквивалентны, т.к. |
||||
|
|
|
Rx |
|
|
|
|
равны главные векторы: |
|
|
|||
|
|
|
|
|
|
|
|
R Rx Ry |
|
||||
|
|
|
|
r |
|
|
|
|
|
||||
|
|
|
|
|
|
и главные моменты относительно произвольно |
|||||||
|
|
Рис.61 |
|
|
|
O |
|
взятого полюса O: |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Mo r R; Mo(Rx) r Rx; Mo(Ry) r Ry. |
|||||||||||
Отсюда получим |
|
|
|
|
|
|
|
||||||
|
|
r R |
x |
r |
R |
y |
r (R R |
y |
) r R M |
o(R) |
, |
||
|
|
|
|
|
|
|
x |
|
|
||||
что и требовалось доказать.
Пример. Вычислить момент относительно полюса O силы P, показанной на рис.62. Раскладываем силу на состав-
l |
P |
|
|
P |
Px |
y |
|
h
 O
O
Рис.62
ляющие Px и Py , плечи которых относительно
полюса известны, поэтому вычислить моменты составляющих не представляет труда.
По теореме Вариньона получим
mo(P) mo(Px) mo(Py)
Pcos h Psin l
54
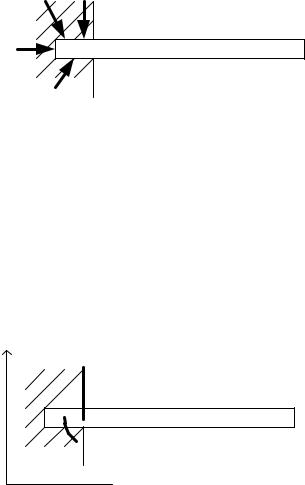
7. Реакция жесткой заделки
Примером жесткой заделки служит жесткое закрепление балки в стене, показанное на рис.63.
R |
R1 |
2 |
|
R3 |
A |
|
|
Rn |
|
Рис.63
На часть балки, замурованной в стену, действует произвольная система сил. Приведем эту систему сил к центру приведения A. В результате приведения произвольной системы сил заменяем ее эквивалентной системой, которая состоит из одной силы, приложенной в точке A, и момента. В силу того, что направление приведенной силы не известно, показываем ее составляющие, направленные по осям координат. Реакция жесткой заделки (приведенная система) показана на рис. 64.
y  YA
YA
 A
A
 XA
XA  mA
mA
 x
x
Рис.64
Момент mA называется моментом в заделке или реактивным момен-
том.
8. Распределенная нагрузка
До сих пор рассматривались силы, приложенные в одной точке. Такие силы называются сосредоточенными. В отличие от сосредоточенных сил, распределенная нагрузка действует на некоторой площади или длине тела. Примеры распределенных нагрузок: ветровая нагрузка, давление воды
55
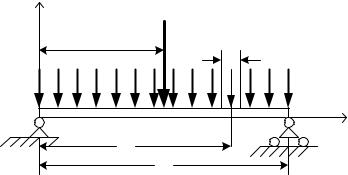
на плотину, давление (вес) слоя сыпучего материала.
Характеризуется распределенная нагрузка интенсивностью, т.е. величиной силы, приходящейся на единицу поверхности действия нагрузки. Обозначается интенсивность q, Н/м.
Распределенная нагрузка всегда представляет собой систему параллельных сил, направленных в одну сторону. Следовательно, распределенная нагрузка имеет равнодействующую. Найдем модуль и точку приложения этой равнодействующей.
y |
Q |
Qi |
|
|
h |
x |
|
||
|
|
|
i |
|
A |
|
|
B |
x |
xi |
l |
|
|
|
|
Рис.65 |
|
|
|
На длине l балки AB действует равномерно распределенная нагрузка интенсивностью q. На рис. 65 нагрузка представлена системой параллельных сил, состоящей из бесконечного числа сил (на рис. показывается ко-
личество векторов сил произвольное). Обозначим равнодействующую Q и определим ее модуль. Система параллельных сил состоит из сил
Q1,Q2,...Qi,...Qk . Т.к. Qi q xi, то Q Qi q xi ql. Найдем, на каком расстоянии h от точки A приложена равнодействующая Q.
По теореме Вариньона |
m |
A(Q) |
mA(Q ) или |
|
|
|
|
||||||
|
|
|
i |
|
|
|
|
||||||
|
|
|
Qh Qixi |
|
|
|
|
||||||
Qh lim qi xi xi |
|
|
|
|
l |
|
|
|
l |
2 |
|
l |
|
Q h q x dx Q h q |
|
Q |
. |
||||||||||
|
|
|
|||||||||||
|
|
|
|
|
0 |
2 |
2 |
|
|||||
Таким образом, Qh Q |
l |
, |
откуда |
h |
l |
. |
|
|
|
|
|||
|
|
|
|
|
|
||||||||
2 2
Следовательно, линия действия равнодействующей равномерно рас-
56
пределенной нагрузки проходит через середину нагрузки (AC 2l) ; модуль
равнодействующей Q ql. |
|
|
|
|
|
|
||||||
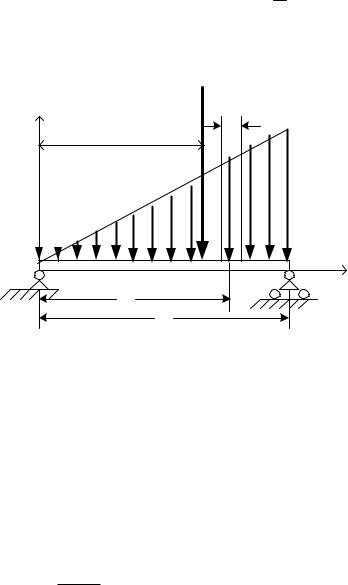
|
На рис.66 на балку AB |
|
|
Q |
|
|
|
|||||
действует |
неравномерно |
|
|
xi |
|
|
||||||
распределенная |
|
нагрузка. |
y |
h |
|
|
||||||
Распределенная |
по закону |
|
|
|
|
|
||||||
треугольника нагрузка, ин- |
|
|
|
|
|
|
||||||
тенсивность |
которой |
воз- |
|
|
|
|
|
|
||||
растает от нуля (в точке |
A) |
|
|
|
|
qmax |
|
|||||
до |
наибольшего |
значения |
|
|
|
|
|
|
||||
qmax в |
точке |
B. |
Найдем |
A |
|
|
|
B |
x |
|||
силу |
Q, |
эквивалентную |
xi |
|
|
|||||||
|
|
|
|
|||||||||
этой нагрузке. |
|
|
|
|
l |
|
|
|
||||
Очевидно, что Q Qi . |
|
|
|
|
|
|||||||
|
|
Рис.66 |
|
|
||||||||
Для |
определения |
модуля |
|
|
|
|
||||||
равнодействующей силы Q выделим на балке участок длиной xi, |
от- |
|||||||||||
стоящий от конца |
A на расстоянии xi . |
Сила, |
эквивалентная нагрузке на |
|||||||||
этом участке,Qi |
qi xi. Интенсивность нагрузки qi |
на этом участке xi |
||||||||||
зависит |
от |
|
положения |
участка |
следующим |
обра- |
||||||
зом: |
qi |
|
qmax |
q |
|
qmax |
x . Тогда |
|
x |
l |
l |
||||||
|
|
i |
|
i |
||||
|
i |
|
|
|
|
|
|
Qqmax x x .
il i i
Определяем модуль силы:
|
q |
max |
|
q |
max |
l |
q |
l2 q |
max |
l |
q |
max |
l |
|||||
Q lim |
|
x x |
|
xdx |
max |
|
|
|
|
|
Q |
|
|
. |
||||
|
l |
|
l |
|
2 |
|
2 |
|
|
2 |
|
|||||||
|
|
i i |
|
0 |
l |
|
|
|
|
|
|
|
||||||
Точку приложения равнодействующей найдем из условия равенства главных моментов эквивалентных систем:
mA(Q) |
mA(Q ) или |
Q h Qixi |
|
qmax |
xi2 xi |
|
|||||
|
i |
|
|
l |
|
57
Q h |
q |
limx2 |
x |
q |
max |
l |
x |
2 |
dx |
q |
max |
|
l3 |
|
|
||||||
|
max |
|
|
|
|
|
|
|
. |
|
|
||||||||||
|
l |
|
l |
|
|
|
l |
3 |
|
|
|||||||||||
|
|
|
i |
i |
|
0 |
|
|
|
|
|
|
|
|
|
|
|||||
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Q h |
|
q |
l2 |
|
|
|
|
|
|
|
q |
|
l |
|
|
|
|
2 |
|
||
|
max |
|
, учитывая, что Q |
|
|
max |
|
, получим h |
|
l. |
|||||||||||
3 |
|
|
|
2 |
|
3 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Следовательно, сила, эквивалентная неравномерно распределенной нагрузке (распределенной по треугольнику), приложена в точке, отстоящей от участка балки, на котором интенсивность нагрузки равна нулю, на расстоянии, равном 2/3 всей длины распределения нагрузки. По модулю эта сила равна половине произведения максимальной интенсивности на длину участка распределения нагрузки.
Вопросы по теме 4 для самоконтроля
1.Какие две системы сил эквивалентны друг другу?
2.Как читается теорема об эквивалентности двух систем сил?
3.Какая система сил называется уравновешенной?
4.Какая сила является равнодействующей системы сил?
5.В каком случае система из двух сил уравновешена?
6.Можно ли силу, не нарушая её действия на тело, переносить по линии её действия?
7.К какому простейшему виду приводится система сходящихся сил?
8.Где находится точка приложения равнодействующей системы сходящихся сил?
9.Как найти по модулю и направлению равнодействующую двух параллельных сил, направленных в одну сторону? Где находится точка
приложения равнодействующей такой системы сил?
10.Как найти по модулю и направлению равнодействующую двух параллельных сил, направленных в разные стороны и не равных по модулю? Где находится точка приложения равнодействующей?
11.Какая система сил образует пару сил?
12.Имеет ли пара сил равнодействующую?
13.Чему равен главный вектор пары сил?
14.Чем измеряется действие на твердое тело пары сил? 15.Чему равен момент пары сил?
16.Как определить знак момента пары сил?
17.Чему равна и как направлена сосредоточенная сила, эквивалентная равномерно распределенной нагрузке; нагрузке, распределенной по
58
треугольнику?
18.Сколько и какие неизвестные величины определяются при нахождении реакции жесткой заделки?
19.К какому простейшему виду приводится произвольная система сил в общем случае?
20.Сформулируйте теорему Вариньона о моменте равнодействующей. 21.Нарушится ли механическое состояние тела при параллельном переносе силы? Чем компенсировать параллельный перенос силы?
22.Какой величиной характеризуется распределенная нагрузка? 23.Чему равна, как направлена и где приложена сосредоточенная сила,
эквивалентная равномерно распределенной нагрузки?
24.Чему равна, как направлена и где приложена сосредоточенная сила эквивалентная распределенной по закону треугольника нагрузке?
59
Тема 5
УСЛОВИЯ И УРАВНЕНИЯ РАВНОВЕСИЯ СИСТЕМЫ СИЛ
Если под действием системы сил тело остается в покое, то такое состояние тела называется состоянием равновесия.
1. Общие условия равновесия тела
Выведем общие условия, при которых твердое тело под действием приложенных к нему сил остается в состоянии покоя.
Механическое состояние тела (как частный случай состояния покоя) не изменится, если к телу приложена уравновешенная система сил. Главный момент относительно произвольного полюса уравновешенной системы сил и главный вектор такой системы равны нулю.
Следовательно, условиями равновесия тела являются равенство
нулю главного вектора этой системы сил и равенство нулю главного момента относительно произвольно выбранного полюса.
2. Скалярные уравнения равновесия твердого тела
По определению главный вектор системы сил равен векторной сумме всех сил системы, т.е.R* Fi ; главный момент относительно некоторо-
го полюса равен геометрической сумме вектор - моментов относительно
|
|
того полюса всех сил системы, т.е. Mo mo(Fi) . |
|
При равновесии системы: |
|
Fi 0; |
(5.1) |
mo(F ) 0. |
(5.2) |
i |
|
Выбрав систему декартовых координат и спроектировав эти векторные равенства на оси координат, получим шесть скалярных уравнений:
(Fi)x 0; (Fi)y 0; (Fi)z 0;
(mo(F ))x 0; |
(mo(F ))y 0; |
(mo(F ))z 0. |
i |
i |
i |
Учитывая, что проекция вектора-момента силы на ось x (или y, или z) равна моменту той же силы относительно оси соответственно x или
60
y |
или z, а |
также обозначив (Fi)x Xi , |
(Fi)y Yi , |
||||
(Fi)z Zi , |
где |
Xi |
проекции на ось x |
сил |
системы, |
||
т.е.F1x ,F2x,F3x,....,Fnx; |
соответственно |
Yi проекции |
на |
ось y, а |
|||
Zi |
проекции сил на ось z, получим уравнения в виде: |
|
|
||||
|
Xi 0; |
Yi 0; Zi 0; |
|
|
(5.3) |
||
|
mx(F ) 0; |
my(F ) 0; mz(F ) 0. |
|
(5.4) |
|||
|
|
i |
|
i |
i |
|
|
Эти уравнения называются уравнениями равновесия произвольной системы сил. Первые три уравнения называются уравнениями проекций, последние – уравнениями моментов.
Следовательно, если тело находится в равновесии, то сумма про-
екций на каждую из координатных осей всех сил, приложенных к этому телу (заданных и реакций), равна нулю; а также равна нулю сумма моментов относительно каждой координатной оси всех сил системы.
3. Частные случаи уравнений равновесия различных систем сил
Система сходящихся сил
Такую систему образуют силы, приложенные к одному телу, если линии
действия всех сил пересекаются в одной точке. |
|
z |
|
|
F1 |
Если все силы перенести по линии их действия |
|
Fn |
|
|
|
в эту точку, то система будет представлена сис- |
|
|
|
y |
|
|
|
||||
темой сил, приложенных в одной точке. Такая |
|
O |
|
||
система показана на рис.67. |
F3 |
|
|||
Принимаем точку приложения сил за на- |
x |
F2 |
|||
чало координат. Очевидно, что моменты отно- |
|
|
|
|
|
сительно осей координат всех сил системы |
|
Рис.67 |
|
||
равны нулю, т.к. линии действия их пересекают |
|
|
|
|
|
ось. |
|
|
|
|
|
Следовательно, уравнения моментов будут иметь место и при неравновесии системы сил, эти уравнения обращаются в тождества. Поэтому
при равновесии системы сходящихся сил достаточными уравнениями равновесия являются уравнения проекций:
61
