
2140
.pdf
Xi N P 0;
Yi RA RB Fтр 0.
Из этих уравнений находим:
RB Fтр 4,7 кН;
2
P N 94кН;
RA RB Fтр 4,7 9,4 14,1 кН.
92
Тема 8
ЦЕНТР ТЯЖЕСТИ
1. Центр параллельных сил
На рис. 97 показана система параллельных сил, не лежащих в одной плоскости. Найдем координаты точки приложения равнодействующей такой системы сил.
z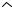 A1 A3
A1 A3
|
|
F1 |
|
|
A2 |
|
|
C |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
F3 |
|
A4 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
|
|
R |
F2 |
|
F |
|||||
|
|
|
|
|
|
|||||
1 |
|
|
|
|
|
|
|
|||
|
|
|
|
y |
|
|
|
4 |
||
|
|
|
|
|
R2 |
|
|
|
||
|
x |
|
|
R |
|
|
||||
|
Рис.97 |
|
|
|
||||||
|
|
|
|
|||||||
|
|
|
|
|
||||||
|
|
|
|
|
||||||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
||||
Система сил включает силы:
F1, приложенную в точке A1 с координатами (x1'y1'z1);
F2, приложенную в точке A2с координатами (x2'y2'z2);
F3, приложенную в точке A3с координатами (x3'y3'z3);
F4, приложенную в точке A4 с координатами (x4'y4'z4).
Сложим силы F1 и F2 изложенным ранее способом сложения двух параллельных сил, лежащих в одной плоскости: F1+F2=R1. Затем сло-
жим аналогичным образом силы R1 |
и F3: R1+F3=R2 |
, а также силы R2 |
и F4: R2+F4=R . В результате F1+F2+F3+F4=R |
. Сила R эквива- |
|
лентна первоначальной системе сил и, следовательно, является равнодействующей этой системы.
93
Обозначим точку приложения равнодействующей буквой C, а её координаты xc, yc,zc . Точка C называется центром параллельных сил и об-
ладает следующим свойством: если вращать каждую силу системы вокруг точки её приложения, не нарушая при этом параллельности сил, то равнодействующая, оставаясь параллельной силам системы, будет вращаться вокруг точки C.
Для определения координат точки C по теореме Вариньона о моменте равнодействующей найдём момент равнодействующей относительно оси
y: my(R) my(F |
) my(F |
) my(F ) my(F ) или |
|
1 |
2 |
3 |
4 |
R xc F1 x1 F2 x2 F3 x3 F4 x4, т.е. R xc Fi xi. |
|||
Учитывая, что R =F1+F2+F3+F4= Fi |
, из этих уравнений найдем |
||
координату x |
Fixi |
. |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
c |
|
|
|
Fi |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Составив уравнение момента равнодействующей относительно оси x, |
|||||||||||||||||||
аналогично получим y |
|
Fi yi |
. |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
c |
|
|
Fi |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Если силы повернуть так, чтобы они стали параллельными оси x, то |
|||||||||||||||||||
из уравнения момента равнодействующей относительно оси y |
найдем |
||||||||||||||||||
координатуz |
c |
|
Fizi |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Fi |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Таким образом, центр параллельных сил |
имеет координаты, |
которые |
|||||||||||||||||
определяются: |
|
|
|
Fixi |
|
|
|
|
Fi yi |
|
|
|
Fizi |
|
|
||||
|
x |
|
; y |
|
; z |
|
|
|
(8.1) |
||||||||||
|
Fi |
|
Fi |
|
Fi |
||||||||||||||
|
c |
|
|
|
c |
|
|
c |
|
|
|||||||||
2. Центр тяжести твердого тела
Разбиваем твердое тело на n элементарных частиц. На каждую частицу действует сила тяжести, и все эти силы образуют систему параллельных сил, которые можно сложить изложенным выше способом. В результате
P Pi , где P вес тела; Pi вес каждой элементарной частицы.
Очевидно, что точка приложения веса тела (центр тяжести тела) является центром параллельных сил, а поэтому координаты центра тяжести оп-
94
ределяются как координаты центра параллельных сил (см. формулу 8.1):
x |
|
Pixi |
; y |
|
|
Pi yi |
; z |
|
|
Pizi |
, |
(8.2) |
|
|
|
|
|
||||||||
c |
|
Pi |
c |
|
Pi |
c |
|
Pi |
|
|||
где xi,yi,zi координаты элементарной i-й части.
Согласно свойству параллельных сил центр тяжести тела не изменяет своего положения относительно тела при любом положении этого тела.
Для однородного тела в формулах вычисления координат центра тяжести вместо веса можно записывать соответствующий объем тела или части тела:
x |
|
Vixi |
; y |
|
Vi yi |
; z |
|
|
Vizi |
. |
(8.3) |
V |
|
|
|
||||||||
c |
|
c |
|
V |
c |
|
V |
|
|||
|
|
i |
|
|
i |
|
|
i |
|
||
3. Центр тяжести однородной плоской фигуры
Плоской фигурой называется такое твердое тело, один из трех размеров которого (толщина тела) настолько мал в сравнении с другими (длиной и шириной), что этим размером можно пренебречь. Если вес единицы площади фигуры , то вес фигуры P S, где S площадь фигуры.
Учитывая также, что вес элементарной частицы фигуры Pi Si ,
выведем формулу для определения координат центра тяжести однородной плоской фигуры:
x |
Sixi |
|
Sixi |
|
|
Sixi |
; аналогично |
y |
Si yi |
. |
|||
|
|
||||||||||||
|
|
|
|
|
|
|
|||||||
C |
Si |
Si |
|
S |
|
|
C |
S |
|||||
|
|
|
|
|
|||||||||
Таким образом, координаты центра тяжести плоской фигуры находят- |
|||||||||||||
ся: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
Sixi |
; y |
Si yi |
. |
|
(8.4) |
|||||
|
S |
|
|
||||||||||
|
|
C |
|
|
C |
S |
|
|
|
||||
Величина SxC Sixi называется статическим моментом пло- |
|||||||||||||
ской фигуры относительно оси y. Соответственно |
SyC Si yi ста- |
||||||||||||
тический момент плоской фигуры относительно оси x.
95
4. Центр тяжести линии
Линией называется такое твердое тело, длина которого настолько велика в сравнении с размерами поперечного сечения, что этими размерами можно пренебречь.
Координаты центра тяжести линии вычисляются:
x |
|
lixi |
; y |
|
|
li yi |
; z |
|
|
lizi |
, |
(8.5) |
|
|
|
|
|
||||||||
C |
|
l |
C |
|
l |
C |
|
l |
|
|||
где li длина одной части линии; l li длина всей линии.
Положение центра тяжести плоской линии определяют две координаты:
x |
|
lixi |
; y |
|
|
li yi |
. |
(8.6) |
|
|
|
||||||
C |
|
l |
C |
|
l |
|
||
Очевидно, что для прямой линии, совпадающей с осью координат, достаточно одной координаты для определения положения центра тяжести.
Следует иметь в виду, формулы (8.5) и (8.6) выведены для тех линий, у которых вес единицы их длины не изменяется (однородных линий).
5. Первая теорема Гюльдена
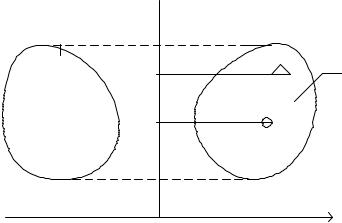
Объем тела вращения, полученного вращением плоской фигуры вокруг оси, лежащей в плоскости фигуры, но не пересекающей ее, равен произведению площади фигуры на длину окружности, описанной ее центром тяжести при этом вращении.
y |
|
|
xi |
S |
1 |
xC |
|
i |
C |
|
|
|
|
|
|
|
x |
Рис.98 |
|
|
Тело 1 (рис.98) вращается вокруг оси y. Замкнутая поверхность, об-
96
разованная при вращении тела, называется поверхностью вращения. Тело, ограниченное этой поверхностью, называется телом вращения.
Разбиваем тело 1 на элементарные частицы. Выделяем на теле 1 элементарную частицу площадью Si . При вращении тела эта площадка обра-
зует круговое кольцо. Сумма объемов колец всех частиц тела равна объему тела вращения. Если xi радиус вращения частицы, то объем кругового
кольца равен Vi 2 xi Si. Так как объем тела вращения V Vi ,
то
V 2 xi Si.
Учитывая, что xi Si SxC(статический момент фигуры относи-
тельно оси y), получим V 2 SxC , где 2 xC длина окружности ра-
диуса xC; S площадь фигуры. Таким образом, V 2 SxC , что и тре-
бовалось доказать. Отсюда координату центра тяжести тела вращения, показанного на рис.98, можно найти как
x |
|
V |
, |
|
2 S |
||||
C |
|
|
||
где V объем тела вращения. |
|
|
|
6. Вторая теорема Гюльдена
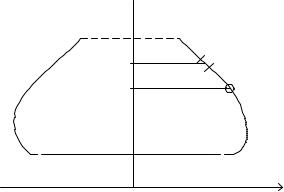
Площадь поверхности вращения, полученной вращением плоской кривой вокруг оси, лежащей в плоскости этой кривой, но её не пересекающей, равна произведению длины этой кривой на длину окружности, описанной ее центром тяжести.
y |
|
A |
|
x |
l |
i |
i |
xC |
|
|
B |
|
x |
Рис.99 |
|
97 |
|
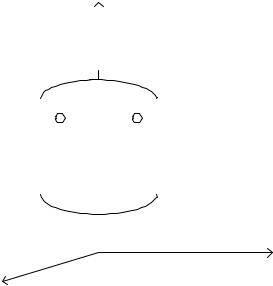
Обозначим: l длина |
кривой AB, li длина одного из элементар- |
ных участков, на которые разбита данная кривая, показанная на рис. 99. Поверхность, которую опишет элементарный участок li кривой ABпри
вращении той кривой вокруг оси y, можно принять за усеченный конус,
боковая поверхность которого Si равна Si 2 xi li. Площадь всей поверхности вращения при этом равна S Si S 2 xi li . Учи-
тывая, что xi li xCl, получим S 2 xCl, что и требовалось дока-
зать. Из этого уравнения следует, что координата центра тяжести кривой AB находится как
x |
|
S |
. |
|
|||
C |
|
2 l |
|
7. Теоремы для определения положения центра тяжести отдельных тел
1-я теорема для тел, имеющих ось симметрии. Если однородное те-
ло имеет ось симметрии, то центр тяжести такого тела находится на
этой оси. |
|
|
|
|
|
|
|
Осью симметрии тела, показан- |
|
z |
|
|
|
||
|
|
|
|||||
ного на рис. 100, является ось z. |
|
|
|
|
|
||
Разбиваем |
тело |
на отдельные |
|
|
|
|
|
элементарные частицы. При этом |
|
|
|
|
|
||
следует отметить, что каждой части- |
|
A |
A1 |
|
|
||
|
|
||||||
це A1, имеющей положительную ко- |
|
x,y,z |
x, y, |
|
z |
||
ординату y1, |
соответствует частица |
|
|
|
|
|
|
A с такой же, но отрицательной ко- |
|
|
|
|
|
||
ординатой. Поэтому |
Vixi 0, где |
|
|
|
|
|
|
Vi объём i- |
й частицы. Рассуждая |
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
аналогичным образом, установим, x |
|
|
|
|
|
||
что Vi yi 0. |
|
|
Рис.100 |
||||
Следовательно, из уравнений (8.3)
имеем xC =0; yC =0, т.е. центр тяжести лежит на оси z, которая является осью симметрии тела, что и требовалось доказать.
98
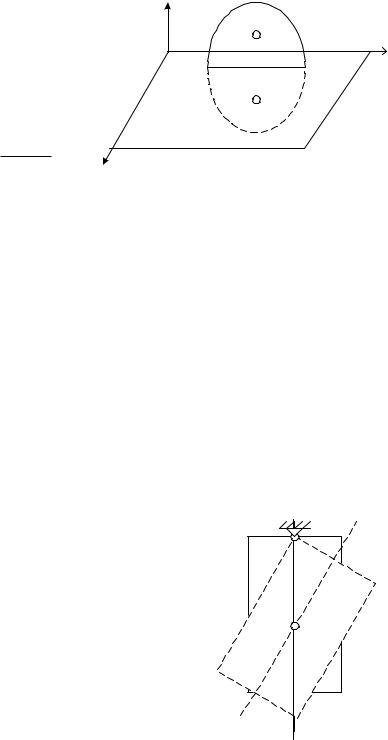
2-я теорема для тел, имеющих плоскость симметрии. Если одно-
родное тело имеет плоскость симметрии, то центр тяжести такого
тела лежит на этой плоскости. |
|
|
|
|||
Координатная плоскость |
xOy является плоскостью симметрии тела, |
|||||
показанного |
на рис.101. Очевидно, |
z |
|
|
||
что каждой |
элементарной |
частицы |
|
|
||
|
|
|
||||
тела A1, имеющей положительную |
|
A1 |
y |
|||
координату |
z, соответствует эле- |
O |
|
|||
ментарная частица A, |
имеющая та- |
|
A |
|
||
кую же, но отрицательную коорди- |
|
|
||||
нату. Поэтому координата |
центра |
|
|
|
||
тяжести тела равна z |
Vizi 0, |
x |
|
|
||
|
|
|
||||
|
C |
V |
|
Рис.101 |
|
|
т.е. центр тяжести тела лежит в
плоскости xOy, являющейся плоскостью симметрии тела. Следствия из 1-й и 2-й теорем:
центр тяжести отрезка прямой находится в его середине;
центр тяжести окружности, круга, шара или сферы находится в геометрическом центре соответственно окружности, круга, шара, сферы;
центр тяжести периметра и площади параллелограмма, ромба, прямоугольника и квадрата находится в точке пересечения диагоналей соответствующей фигуры;
центр тяжести периметра и площади правильного многоугольника находится в центре вписанной в него окружности или круга.
8.Методы определения положения центра тяжести тела
Экспериментальный метод. Способов экс-
периментального определения положения центра тяжести множество. Рассмотрим только некоторые из них.
1.Положение центра тяжести тела (рис.102) определяется подвешиванием тела с изменением точек подвеса. Фиксируя на теле линию отвеса (вертикаль, проходящую через точку подвеса тела) при различных положениях тела, находим точку пересечения этих линий, где и находится центр масс тела.
A |
B |
|
C |
|
Рис.102 |
99
|
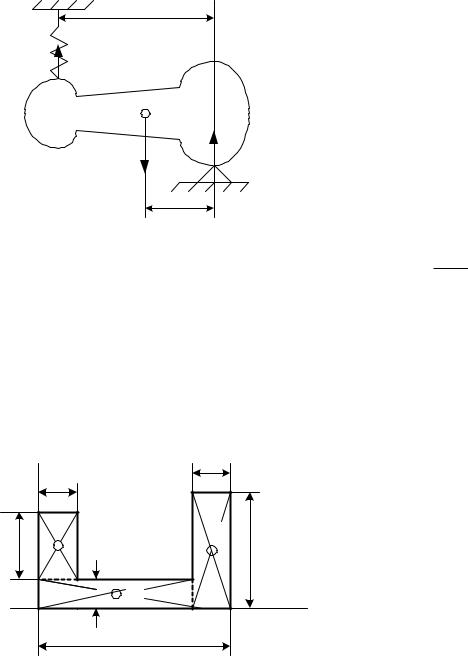
2.Экспериментально положение центра тяжести тела можно найти |
||||||||
|
|
l |
|
из уравнения равновесия тела, располо- |
|||||
|
|
|
|
жив тело соответствующим образом. |
|
||||
|
RA |
|
|
|
Показанное на рис. 103 тело опи- |
||||
|
|
|
рается в точке |
B на остриё, а в точке |
A |
||||
|
A |
C |
|
подвешено на пружинных весах, показы- |
|||||
|
|
|
|||||||
|
|
|
RB |
вающих реакцию RA в точке A. Замером |
|||||
|
|
P |
B |
получены вес тела P и расстояние между |
|||||
|
|
|
опорами l. Из уравнения равновесия тела |
||||||
|
|
xc |
|
||||||
|
|
|
m Px R l 0 находим координа- |
||||||
|
|
|
|
B |
c |
A |
|
|
|
|
Рис.103 |
|
ту центра тяжести тела: |
|
|
||||
|
|
|
|
x |
RAl . |
|
|||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
c |
P |
|
|
|
Метод разбиений. При этом способе тело, центр тяжести которого |
|
|||||||
нужно определить, «разбивают» на отдельные части, положения центров |
|
||||||||
тяжестей которых известны или могут быть предварительно найдены. |
|
||||||||
Вычисления производят по формулам (8.2) (8.6), выбрав из них соответ- |
|||||||||
ствующую формулу. |
|
|
|
|
|
|
|
||
|
Пример 1. |
Вычислить координаты центра тяжести однородной пло- |
|||||||
|
y |
|
2 |
|
ской |
фигуры, |
показанной |
на |
|
|
|
|
рис.104. Размеры указаны в сан- |
||||||
|
2 |
|
|
|
тиметрах. |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
C1 |
|
C3 |
|
Разбиваем |
фигуру на три |
|||
3 |
|
|
прямоугольника, т.к. положение |
||||||
1,5 |
|
|
6 |
||||||
|
|
|
центра тяжести прямоугольника |
||||||
|
|
|
|
|
|||||
|
|
C2 |
|
|
известно. Учитывая, что центр |
||||
|
|
|
|
|
x тяжести прямоугольника нахо- |
||||
|
|
10 |
|
|
дится в точке пересечения его |
||||
|
|
|
|
|
диагоналей, показываем их по- |
||||
|
Рис.104 |
|
|
ложения, обозначив соответст- |
|||||
|
|
|
|
|
венно C1,C2,C3. |
|
|||
Записываем значения координат каждой из этих точек (в см):
x1 1,y1 3; |
|
x2 4,y2 0,75 |
|
x3 9,y3 3. |
||||
Вычисляем площадь каждой фигуры: |
|
S |
|
12см2 . |
||||
S 6см2 |
, |
S |
2 |
12см2 |
, |
3 |
||
1 |
|
|
|
|
|
|
||
100
|
Для вычисления координат центра тяжести плоской фигуры восполь- |
|||||||||||||||
зуемся формулами (8.4), которые для рассматриваемой задачи имеют |
||||||||||||||||
вид:x |
S1x1 S2x2 S3x3 |
61 12 4 129 5,4см; |
|
|||||||||||||
|
C |
|
S1 S2 S3 |
|
|
|
6 12 12 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||
y |
S1y1 S2y2 S3y3 |
63 120,75 123 2,1см. |
|
|||||||||||||
C |
|
|
S1 S2 S3 |
|
|
|
|
6 12 12 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
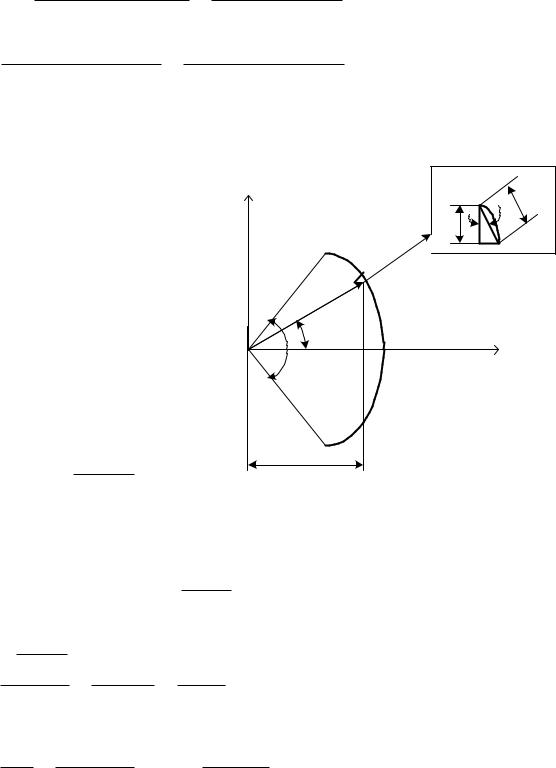
Пример 2. Используя метод разбиений, выведем формулу для вычис- |
|||||||||||||||
ления координат центра тяжести |
|
|
|
|
|
|
|
|||||||||
дуги, радиуса R (рис.105). Раз- |
y |
|
|
|
|
|
li |
|||||||||
биваем дугу |
AB на |
n частей, |
|
|
|
|
yi |
|||||||||
|
|
|
|
|
||||||||||||
каждая часть длиной li . Одна |
|
|
A |
|
|
|
||||||||||
|
|
|
|
|
|
|||||||||||
из таких частей показана. |
|
|
|
|
|
R |
li |
|
|
|||||||
Число |
разбиений |
выбрано |
|
|
|
|
||||||||||
так, |
что |
каждую часть |
можно |
|
|
|
|
|
|
|
||||||
принять за отрезок прямой. |
То- |
|
|
|
|
|
x |
|||||||||
|
2 |
|
|
|
|
|||||||||||
гда для вычисления координаты |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|||||||||||
центра тяжести этой дуги можно |
|
|
|
|
|
|
|
|||||||||
применить формулу (8.6) . |
|
|
|
|
|
|
|
|
|
|||||||
|
Находим координату |
|
|
|
xi |
B |
|
|
|
|
||||||
|
|
x lixi |
, |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
Рис.105 |
|
||||||
|
|
|
C |
|
l |
|
|
|
|
|
|
|
|
|
||
где li |
|
|
|
|
|
|
xi координата центра тяжести этой части. |
|||||||||
длина одной части; |
||||||||||||||||
Учитывая, |
что длина дуги l R 2 , |
где |
2 центральный угол в |
|||||||||||||
радианах, а также что l |
yi |
, |
вычисляем |
|
|
|
|
|||||||||
|
|
yixi |
|
|
i |
|
cos |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
R y |
|
y |
|
|
|
|
|
|
|
|||
x |
|
cos |
|
|
, |
где y AB, а длина хорды может |
||||||||||
|
|
|
i |
|
i |
|||||||||||
C |
|
R 2 |
|
R 2 |
|
|
2 |
|
|
i |
|
|
|
|
||
|
|
|
|
|
|
AB 2Rsin . |
|
|||||||||
быть |
|
представлена |
|
|
|
как |
|
Тогда |
||||||||
x |
AB 2Rsin x |
Rsin . При этом y |
|
0. |
|
|||||||||||
C |
2 |
|
2 |
|
C |
|
|
|
|
|
|
C |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
101 |
|
|
|
|
|
