
2140
.pdf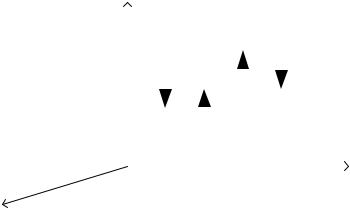
Xi 0; |
Yi 0; |
Zi 0. |
(5.5) |
Если же силы лежат в плоскости xOy, то обращается в тождество еще
и уравнение проекций на ось Oz. Поэтому для плоской системы сходя-
щихся сил уравнениями равновесия являются:
|
|
|
Xi 0; |
Yi 0. |
|
|
(5.6) |
||
|
|
Система параллельных сил |
|
||||||
|
|
|
|
|
|
|
|
Линии действия всех |
|
z |
|
|
|
|
|
|
сил |
такой системы |
парал- |
|
|
|
|
|
|
||||
|
|
|
|
|
|
||||
|
|
|
|
Fn |
лельны между собой. Сис- |
||||
|
|
|
|
|
|||||
|
F1 |
|
F3 |
|
тема |
параллельных |
сил, |
||
|
|
|
|
|
показана на рис.68. Систе- |
||||
|
|
|
|
|
|
|
ма координатных осей вы- |
||
|
|
|
|
|
|
|
|||
|
|
F2 |
|
|
|
|
брана нами так, что ось |
||
|
|
|
|
|
|
||||
O |
|
|
|
y |
Oz |
параллельна |
силам. |
||
|
|
|
|||||||
|
|
|
|
При таком выборе осей об- |
|||||
|
|
|
|
|
|
|
ратятся в тождества урав- |
||
|
|
|
|
|
|
|
|||
x |
|
|
|
|
|
нения проекций сил на оси |
|||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
Ox и Oy, а также уравне- |
||
|
|
Рис.68 |
|
|
ние |
моментов относитель- |
|||
|
|
|
|
|
|
|
но оси Oz.Следовательно, |
||
уравнениями равновесия системы параллельных сил, не лежащих в одной плоскости, являются:
Zi |
0; mx(F ) |
0; my(F ) 0. |
(5.7) |
|
i |
i |
|
Если же все силы системы лежат в одной плоскости, например, в плоскости zOy, то из этих уравнений обращается в тождество еще и уравнение моментов относительно оси Oy, т.к. момент каждой силы относительно оси равен нулю, если линия действия силы пересекает эту ось.
Таким образом, при равновесии плоской системы параллельных
сил составляются два независимых уравнения равновесия:
Zi 0; |
(5.8) |
mo(Fi) 0. (5.9)
62
Уравнение mo(F ) 0 равноценно уравнению mx(F ) 0. |
|
|
|
|
||||||||||||
i |
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
Произвольная плоская система сил |
|
|
|
|
||||||||||||
Все силы такой системы лежат в одной плоскости и расположены |
||||||||||||||||
произвольным образом. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Плоскость действия сил – |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||
координатная плоскость |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F3 |
|||||
xOy (рис.69). |
|
|
|
|
F |
|
|
|
F |
|
|
|||||
Очевидно, из 6-ти общих |
|
|
1 |
2 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
уравнений равновесия |
обра- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
щаются в тождество уравне- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ния проекций на ось |
Oz и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fn |
|
|
|
|
|||||||
уравнения моментов относи- |
|
|
|
|
|
|
|
|
|
|||||||
тельно осей Ox и Oy. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
|
|
|
|
|
|
|
|
|
|||||
Вместо уравнения мо- |
|
|
|
|
|
|
|
|
|
x |
||||||
ментов относительно оси Oz |
|
|
|
|
|
|
Рис.69 |
|
|
|
|
|||||
следует составлять |
равно- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ценное ему уравнение моментов относительно полюса O.
Итак, для находящейся в равновесии произвольной плоской сис-
темы сил, достаточными являются три независимых уравнения: |
|
|
Xi 0; Yi 0; |
mo(F ) 0. |
(5.10) |
|
i |
|
4. Уравнения равновесия сил, приложенных к механической системе, состоящей
из нескольких тел
Механическая система из нескольких абсолютно твердых тел, соединенных между собой какой-либо связью, называется сочлененной системой. Силы, действующие на сочлененную систему, можно разбить на две группы. Внешние силы–силы, с которыми тела, не входящие в сочлененную систему, действуют на рассматриваемую конструкцию. К ним же относятся и реакции связей, за исключением реакций тех связей, которые соединяют тела в систему в местах сочленения тел. Внутренние силы–это силы взаимодействия между телами, образующими сочлененную систему.
При рассмотрении равновесия механической системы, состоящей из нескольких тел, наряду с рассмотрением всей системы в целом, можно ее расчленить и рассматривать равновесие тел в отдельности.
63
Поясним сказанное на примере сочлененной системы, показанной на рис.70.
|
|
|
|
|
P |
|
|
|
|
|
|
|
RC |
|
B |
|
|
|
|
|
|
|
|
YD |
|
|
|
YA |
|
|
|
C |
|
|
|
|
|
|
|
B1 |
|
|
D |
|
|
|
|
|
|
|
|
XD |
|
|
|
300 |
|
|
|
|
|
|
|
A |
X |
a |
|
3a |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|||
|
|
|
|
A |
|
|
|
|
|
|
|
|
Рис.70 |
|
|
|
|
Наклонная балка AB, на конец которой действует сила P, середи- |
||||||||
ной B1 |
опирается на ребро консоли балки CD. Весом балок пренебречь. |
|||||||
Конструкция состоит из двух тел: балки AB и балки CD. Связи на |
||||||||
всю конструкцию наложены в точках |
A,C,D. |
По отношению ко всей |
||||||
конструкции сила P и реакции связей в точках A,C,D относятся к силам |
||||||||
внешним. Давление же балки AB на балку CD, как и реакция балки CD |
||||||||
в точке B1 являются силами внутренними сочлененной системы. При этом |
||||||||
следует принимать во внимание аксиому о равенстве действия и противо- |
||||||||
действия, согласно которой эти силы равны по модулю и противоположно |
||||||||
|
|
|
P |
|
направлены. |
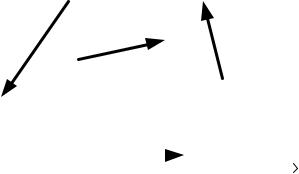
Если |
рассматривать |
|
|
|
|
|
равновесие всей сочлененной систе- |
||||
|
|
|
|
|
||||
|
|
|
|
B |
мы в целом, то внутренние силы в |
|||
|
|
|
|
уравнение равновесия не войдут, так |
||||
|
RВ |
|
|
|
||||
YA |
|
|
|
как они будут «попарно сокращать- |
||||
|
|
|
|
ся». |
из конструкции выде- |
|||
|
B1 |
|
|
|
|
Если же |
||
|
|
|
|
лить одно из тел, например, балку |
||||
|
|
|
|
|
||||
A |
300 |
|
|
|
AB(рис.71), |
то к |
внешним силам, |
|
XA |
|
|
|
действующим на это тело, относятся |
||||
|
|
|
|
|||||
|
Рис.71 |
|
|
сила P, реакции шарнира A и реак- |
||||
|
|
|
|
|
|
|
||
|
|
|
|
|
64 |
|
|
|

ция в точке B1 (результат действия балки CD).
Независимых уравнений равновесия для сочлененной системы увеличивается в n раз. Так для произвольно плоской системы сил, приложенных к сочлененной механической системе из n тел, независимыми являются 3n уравнений равновесия. Поэтому для рассматриваемой задачи можно составить 6 независимых уравнений равновесия.
5.Нестандартные уравнения равновесия произвольной плоской системы сил
Для произвольной плоской системы сил уравнения равновесия
Xi 0, |
Yi 0, |
mo(F ) 0 |
|
|
i |
называются стандартными. Докажем, что вместо этих уравнений при некотором дополнительном условии можно составлять нестандартные уравнения
m |
A(Fi) |
0, |
m |
B(Fi) |
0, |
m |
0 |
(5.11) |
|
|
|
|
C(Fi) |
|
|
или уравнения
mA(F ) 0 |
mB(F ) 0 |
Xi 0. |
(5.12) |
i |
i |
|
|
Согласно общим условиям равновесия, должны быть равны нулю главный вектор системы сил и ее главный момент относительно произвольно выбранного полюса. При этом следует иметь в виду, что при равенстве нулю главного вектора, главный момент не будет зависеть от выбора
полюса MA MB AB R (см. «Зависимость главного момента от выбора полюса»), если R 0, то MA MB. Однако MA MBтакже и тогда, когда R 0, но направлен главный вектор по прямой AB(рис.72).
B
R
A 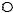
Рис.72
65
Следовательно, дополнительными условиями при составлении нестандартных уравнений равновесия являются:
точки, относительно которых составляются уравнения моментов, не должны лежать на одной прямой, при составлении трёх уравнений моментов;
ось X , на которую проектируются силы, нельзя выбирать перпендикулярно прямой AB, проведенной через полюсы, относительно которых составляются уравнения моментов, в системе уравнений:
mA(F ) 0, |
mB(F ) 0, |
Xi 0. |
i |
i |
|
6. Статически определенные и статически неопределенные задачи
Найдите в предыдущих параграфах ответы на следующие вопросы:
1.Сколько независимых уравнений равновесия можно составить, если тело находится в равновесии под действием произвольной системы сил? (6 уравнений равновесия).
2.Какое количество независимых уравнений равновесия можно составить, если в равновесии под действием произвольной системы сил находится сочлененная система из n тел? (6n уравнений).
3.Сколько независимых уравнений равновесия составляется в случае, если силы, приложенные к такой сочлененной системе, лежат в одной плоскости? (3n).
4.Сколько независимых уравнений равновесия составляется в случае, если силы, приложенные к такой сочлененной системе, лежат в одной плоскости и параллельны между собой? (2n).
5.Сколько независимых уравнений равновесия имеет пространственная система сходящихся сил? (3n)
6.Сколько независимых уравнений равновесия имеет система сходя-
щихся сил, лежащих в одной плоскости? (2n)
Чтобы задача имела решение методами статики, количество по условию задачи неизвестных величин не должно превышать количества независимых уравнений равновесия для рассматриваемой системы сил.
Задачи, в которых число неизвестных не превышает числа независимых уравнений равновесия для данной системы сил, называются статически определенными.
Статически неопределенными называются задачи с числом неизвестных, превышающим число уравнений равновесия. Такие задачи методами статики решения не имеют.
66

7. Методика решения задач статики |
|
||
Все задачи на равновесие твердых тел решаются по одной методике. |
|||
Порядок решения следующий: |
|
|
|
1.Следует выбрать тот материальный |
|
|
|
объект, равновесие которого надо рас- |
|
|
|
смотреть для определения искомых неиз- |
|
B |
|
вестных величин. Такими объектами мо- |
|
l |
|
гут быть одно твердое тело, или сочле- |
|
|
|
ненная система тел, или узел (точка), к |
|
|
|
которому приложены силы. |
h |
30 |
|
2.Необходимо указать (показать на |
|
||
|
|
||
рисунке) все внешние силы, действую- |
|
|
|
щие на выбранный материальный объект |
|
A |
C |
(не обращая внимания на множество всех |
|
|
|
|
|
|
|
внутренних сил). К указанным силам от- |
|
|
|
носятся активные силы, которые, как |
|
|
|
правило, известны, а также неизвестные |
|
Рис.73 |
|
реакции внешних связей. Реакции следу- |
|
|
|
ет направить соответственно типу связи (см.стр.31). |
|
|
|
3.Установить, к какому виду относится система внешних сил, дейст- |
|||
вующих на рассматриваемый материальный объект, и записать для нее со- |
|||
ответствующие уравнения равновесия. |
|
|
|
4. Решить систему составленных уравнений равновесия и определить |
|||
искомые величины. |
|
|
|
Рассмотрим решение следующей задачи по приведенной методике. |
|||
На рис. 73 показана однородная балка |
|
|
|
весом Q и длиной l. Балка опирается |
y |
|
|
одним концом на гладкий пол, а проме- |
|
RB |
|
|
|
||
жуточной точкой B на столб высотой |
|
B |
|
h. Удерживается в положении равнове- |
|
l |
|
сия веревкой AC, протянутой по полу. |
|
30 |
|
Пренебрегая трением, определить на- |
h |
|
RC |
тяжение веревки, реакции пола и стол- |
|
||
ба. |
|
Q |
|
Решение задачи |
|
|
|
|
AT |
C |
|
1. Рассмотреть равновесие балки. |
|
||
2. К активным силам, действующим на |
|
|
x |
|
|
|
|
балку, относится сила тяжести балки |
|
|
|
Q. |
|
Рис.74 |
|
67 |
|
|
|

Показать силу Q на рис.74, направив силу тяжести Q вертикально
вниз и приложив её в середине балки. Так как в точках B и C наложены связи, то «отбросив связи», показать на рис.74 реакции этих связей
RB,RC,T , направив их соответствующим образом (см. стр.31).
3. Силы, приложенные к балке, образуют плоскую произвольную систему сил, для которой составляются три уравнения равновесия:
Xi RB cos30o T 0;Yi RB sin 30o Rc Q 0;
mC RB BC Q 2l cos60o 0 RB cosh30o Q 2l cos60o 0.
4.Решить уравнения и найти в результате решения величины по условию задачи:
R Q l cos60o cos30o |
; |
R Q R sin30o; |
T R |
B |
cos30o. |
||
B |
2h |
|
c |
B |
|
|
|
|
|
|
|
|
|
|
|
Вопросы по теме 5 для самоконтроля
1.Каковы общие условия равновесия твердого тела?
2.Запишите скалярные уравнения равновесия твердого тела в общем случае.
3.Какие уравнения равновесия составляются при равновесии тела, на которое действует система сходящихся сил и если все силы лежат в одной плоскости? Не лежат в одной плоскости
4.Как записать стандартные уравнения равновесия плоской системы сил в общем случае; в частном случае системы параллельных сил, если все силы лежат в одной плоскости? Не лежат в одной плоскости?
5.Какие уравнения равновесия плоской системы сил относятся к нестандартным уравнениям? Какие дополнительные условия следует соблюдать при их составлении?
6.Сколько независимых уравнений равновесия можно составить для механической системы, состоящей из нескольких тел?
7.В каком случае задача не имеет решения методами статики?
8.Какие уравнения равновесия составляются для произвольной пространственной системы сил?
68
Курсовые работы по темам 1-5
Все задания для курсовых работ приведены в приложении.
Курсовая работа С-1
Определение реакций опор твердого тела
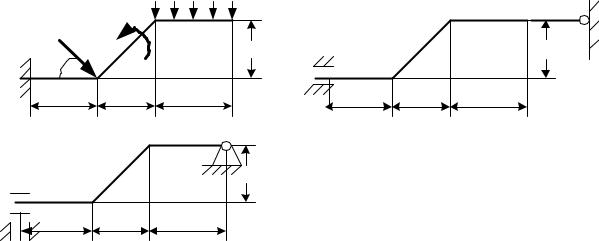
На рисунках к заданию С-1 (см. Приложение) для каждого варианта задания показан брус, ось которого – ломаная линия. Все активные силы, приложенные к брусу, известны и одинаковые на всех трех схемах рисунка. На схеме «а» рисунка к заданию активные силы показаны; на схемах «b» и «с» их нужно показать.
Обратите внимание, что способы закрепления бруса на схемах «а», «b» и «с» различны.
Определить реакции опор для того способа закрепления бруса, при котором исследуемая реакция, указанная в вашем варианте задания, имеет наименьший модуль.
Методика выполнения курсовой работы С–1
Пример (рис.75). Выполнить курсовую работу, если дано: P=5 кН; M =8 кН м; интенсивность распределенной нагрузки q=1,2 кН/м, иссле-
дуемая реакция Ma.
При выполнении курсовой работы нужно записать условие задачи, записать данные Вашего варианта задания, выполнить рисунки к заданию.
a) |
B |
C |
b) |
B |
C |
P |
M |
2 |
|
|
2 |
450 |
|
A |
|
||
A |
2 |
2 |
2 |
2 |
|
2 |
2 |
||||
c) |
B |
C |
|
|
|
|
|
2 |
|
|
|
A |
|
|
|
|
|
2 |
2 |
2 |
|
|
|
|
|
|
Рис.75 |
|
|
1.Выполнить схему «а». На рис.76 показаны активные силы, действующие на брус AC, равновесие которого в задаче рассматривается. При этом равномерно распределенная нагрузка на участке BC заменена
69
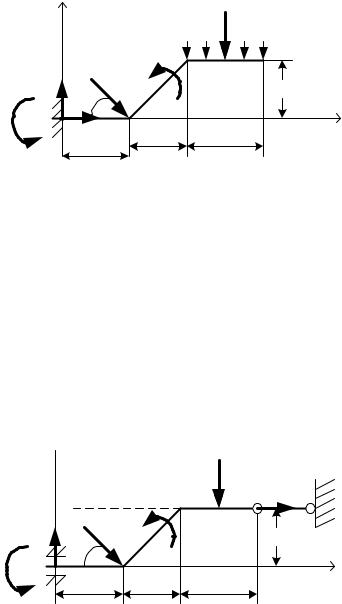
сосредоточенной |
силой |
(см. |
«Распределенная |
нагруз- |
|
ка»):Q q 2 1,2 2 2,4кН. |
|
|
|
|
|
2.Показать реакции связей соответственно типу связи (см. «Типы свя- |
|||||
зей и направление реакций). Связь в точке |
A называется жесткой задел- |
||||
кой. Реакция содержит три величины: XA,YA,mA. |
|
|
|||
a) |
y |
|
Q |
|
|
YA P |
M B |
C |
|
|
|
|
|
|
|
||
mA |
450 |
|
2 |
x |
|
A |
|
|
|
|
|
|
2 XA |
2 |
2 |
|
|
|
|
Рис.76 |
|
|
|
3.Для системы сил, произвольно расположенных в одной плоскости, |
|||||
можно составить не более трех независимых уравнений равновесия. |
|
||||
Однако искомый момент в заделке mAможно найти, составив одно |
|||||
уравнение: |
|
|
|
|
|
mA mA Pcos45 2 M Q 5 0 |
|
||||
mA Pcos45 2 M Q 5 5cos45 2 8 2,4 5 |
|
||||
=11,07 кН м. |
|
|
|
|
|
4. Выполнить схемы «b.» (рис.77) |
|
|
|
||
b) y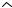
YA |
K |
P |
|
mA |
450 |
A |
2 |
|
|
Q |
|
C RC |
M |
2 |
|
x |
2 |
2 |
Рис.77 |
|
На рис.77 показать активные силы, действующие на брус AC, и реакции опор: жесткой скользящей в точке A и опорного стержня в точкеC.
70
5. Для определения mAсоставить уравнение моментов относительно
полюса, который следует выбрать так, чтобы другие неизвестные в уравнение не вошли:
mК mA Pcos45 2 Pcos45 2 M Q 5 0 mA M Q 5 8 2,4 5 4 кН м.
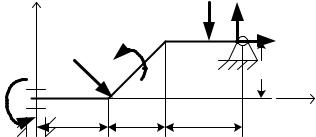
6. Выполнить схему «c» (рис.78). Показать активные силы, действующие на брус AC, и реакции опор: свободной заделки в точке A и неподвижного шарнира в точкеC.
c) |
|
y |
|
Q |
YC |
|
|
M |
B |
|
C |
XC |
|
|
|
|
||||
|
|
P |
|
|
2 |
|
mA |
|
450 |
|
|
x |
|
A |
|
|
|
|||
2 |
2 |
|
2 |
|
||
|
|
|
|
|||
|
|
|
Рис.78 |
|
|
|
Находим mAиз уравнения моментов относительно полюса C:
mC mA Pcos45 2 Pcos45 4 M Q1 0
mA Pcos45 6 M Q 1 5cos45 6 8 2,4 1
31,61кН м.
7.Сравнив значения mA, находим, что наименьший момент получил-
ся при закреплении бруса по схеме b.
8. Составить для схемы b остальные уравнения равновесия и определить реакции YA,RC.
Xi Pcos45 Rc 0 RC Pcos45 5cos45 3,54кН.
Так как реакция отрицательная, следовательно, правильное направление реакции противоположно показанному направлению этой реакции на рис.78.
71
