
2140
.pdf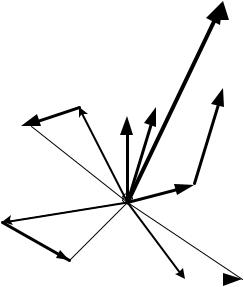
По уравнению (3.2) вычисляется модуль вектор-суммы.
Направление этого вектора определяют косинусы углов (направляющие косинусы):
cos |
R |
x |
; |
cos |
Ry |
; |
cos |
R |
z |
. |
(3.3) |
|
|
R |
|
|
|||||||
|
R |
|
|
|
R |
|
|||||
2. Главный вектор системы сил
Главным вектором системы сил называется векторная сумма всех сил системы, полученная графическим или аналитическим способом:
R* F . |
(3.4) |
i |
|
3. Главный момент системы сил относительно некоторого полюса
Сложить изложенными выше способами можно не только силы, но и вектормоменты сил относительно полюса.
Главным моментом системы сил относительно некоторого полюса называется геометрическая сумма вектор-моментов относительно этого полюса всех сил системы:
|
|
|
|
|
|
|
|
Mo mo(Fi) . |
|
(3.5) |
|
Вычислим главный момент относительно полюса O системы сил, по- |
|||||
|
|
|
казанных на рис. 47. |
||
|
MO |
|
Чтобы вычислить главный мо- |
||
|
|
||||
|
|
мент относительно некоторого полю- |
|||
|
m |
|
са O системы, состоящей из |
||
A1 |
m O(F3) |
|
сил F F F , |
нужно найти вектор- |
|
|
|||||
F1 |
O(F2) |
1 2 |
3 |
|
|
r1 |
|
момент каждой из сил относительно |
|||
|
|
полюса O, т.е. |
|
||
r3 |
|
m |
|
|
|
|
|
F |
|
||
O |
|
|
|
m |
r1 |
; |
|||||
A3 |
|
O(F1) |
|
|
|
o(F1) |
1 |
|
|||
F3 |
r2 |
|
|
|
mo(F2) |
r2 F2; |
mo(F3) r3 F3, |
||||
|
A2 |
|
|
F2 где r ,r ,r |
радиусы-векторы, опре- |
||||||
|
|
||||||||||
|
Рис.47 |
|
|
|
1 |
2 |
3 |
|
|
полюса O |
|
|
|
|
|
деляющие |
относительно |
||||||
|
|
|
|
|
|||||||
|
|
|
|
|
42 |
|
|
|
|
|
|
точку приложения соответствующей силы. Находим геометрическую сумму этих вектор-моментов. Сложение вектор-моментов ничем не отличается от вышеизложенного способа сложения сил. Таким образом, главный момент системы сил относительно полюса O равен:
|
|
|
|
MO mo(F1) |
mo(F2) |
mo(F3) |
или Mo mo(Fi) . |
4. Зависимость главного момента от выбора полюса
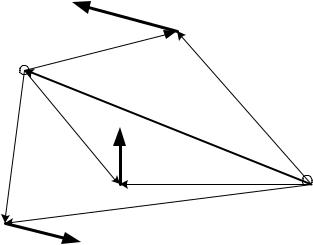
Главный момент системы сил зависит от положения полюса. Выведем эту зависимость. Система сил, показанных на рис.48, состоит из сил
F1,F2,F3.
Главный момент относительно полюса O этой системы сил
MO r1 F1 r2 F2 r3 F3.
|
F1 |
B |
|
|
r1 |
|
|
O |
|
|
|
|
|
r1A |
|
|
|
|
|
r3 |
r2 |
F2 r |
A |
|
r |
2A |
|
D |
C |
|
|
3A |
F3 |
|
|
|
|
|
Рис.48
Главный момент относительно полюса A равен
M |
A |
r |
F r |
F r |
F . |
|
|
1A |
1 2A |
2 |
3A |
3 |
|
Из векторного треугольника OABимеем: r |
r |
AO, из векторного |
||||
|
|
|
|
1A |
1 |
|
|
|
|
43 |
|
|
|
треугольника OCA соответственно: r |
r |
AO; запишем также из |
|
векторного треугольника ODA: r |
2A |
2 |
|
r |
AO. |
||
3A |
3 |
|
|
Следовательно,
MA r1 F1 AO F1 r2 F2 AO F2 r3 F3 AO F3,
т.е.
MA (r1 F1 r2 F2 r3 F3) AO (F1 F2 F3).
Учитывая, что
F1 F2 F3 R,
а также то, что
r1 F1 r2 F2 r3 F3 MO ,
где R главный вектор системы сил,
получим зависимость
MA MO AO R, |
(3.6) |
т.е. главный момент системы сил относительно нового полюса A в сравнении с главным моментом относительно полюса O увеличивается на величину, равную вектор-моменту относительно нового полюса A главного вектора системы сил, если бы главный вектор был приложен в точке O.
44
Вопросы по теме 3 для самоконтроля
1.Какие силы образуют систему сил?
2.Какие силы образуют плоскую систему сил? Какие силы образуют пространственную систему сил?
3.Какая система сил называется системой сходящихся сил, системой параллельных сил, произвольной системой сил?
4.Как находится главный вектор системы сил?
5.Имеет ли главный вектор системы сил точку приложения или он может быть приложен в любой точке?
6.Как аналитически вычислить главный вектор системы сил по модулю и направлению?
7.Какая величина называется главным моментом системы сил относительно полюса?
8.Зависит ли главный момент системы сил от положения полюса?
9.Как графически найти сумму нескольких сил?
10.Запишите и объясните, как связаны между собой главные моменты одной и той же системы сил относительно разных полюсов.
45
Тема 4
ЭКВИВАЛЕНТНЫЕ ПРЕОБРАЗОВАНИЯ СИСТЕМЫ СИЛ
1. Определение эквивалентности двух систем сил. Уравновешенная система сил. Равнодействующая системы сил
Две системы сил эквивалентны друг другу, если при замене одной из них другой механическое состояние тела не изменится. При этом под механическим состоянием понимается состояние покоя тела либо состояние движения. При движении механическое состояние считается неизменным, если не изменяются параметры движения.
Если система сил эквивалентна нулю, то такая система сил называется
уравновешенной.
Механическое состояние тела не изменяется, если уравновешенная система сил перестает или начинает действовать на тело.
Если существует одна сила, эквивалентная системе сил, то эта сила называется равнодействующей этой системы сил.
2.Теорема об эквивалентности двух систем сил
Для эквивалентности двух систем сил необходимо и достаточно, чтобы были равны их главные векторы и их главные моменты относительно произвольно выбранного полюса.
3. Аксиома о равновесии двух сил
Система, состоящая из двух сил, действующих по одной прямой, равных по модулю и противоположно направленных, уравновешена, т. е. система сил эквивалентна нулю, так как равны нулю главный вектор этой системы и главный момент относительно любого полюса.
F1
 F2
F2
Рис.49
46

4. Аксиома о присоединении или исключении уравновешенной системы сил
Если к твердому телу, находящемуся под действием некоторой системы сил, присоединить уравновешенную систему или исключить такую систему, то механическое состояние тела не изменится.
Следствие из аксиомы. Силу, не нарушая ее действия на тело, можно переносить по линии ее действия в любую точку тела.
На рис.50 показаны три системы сил, одна из которых состоит из од-
ной силыF, другая, кроме силы F, включает еще и уравновешенные ме-
жду собой силыP,P1, третья состоит из силыP. Все силы равны по моду-
лю. Так как силы F,P1 уравновешены, то они могут быть отброшены. В
результате получим одну силу P, которая является ничем иным, как силой
F, перенесенной в точку B по линии своего действия.
F A P B P1
. |
Рис.50 |
|
Предлагается студенту самостоятельно, определив главные векторы и главные моменты этих систем, доказать, что новая система, состоящая из
силыP, эквивалентна первоначальной системе, состоящей из силыF.
5. Приведение системы сил к простейшему виду
Приведение системы сил к простейшему виду означает замену одной системы сил другой эквивалентной системой, состоящей из наименьшего количества сил. Наименьшее количество сил для различных систем различно.
Система сходящихся сил приводится к равнодействующей
Существует одна сила, эквивалентная системе сходящихся сил, эта сила является равнодействующей этой системы.
Система сходящихся сил, состоящая из сил F1,F2,Fn, показана на рис. 51. Линии действия этих сил пересекаются в одной точке O. Если пе-
47

ренести каждую силу по линии ее действия в точку O, то получим систему сил, приложенных в одной точке. Сложив по правилу векторного сло-
|
|
R |
|
жения силы F1 и |
F2, получим |
R1; |
|
|
F1 |
1 |
|
сложив эту силу и силуF3, получим |
|||
|
F2 |
|
|||||
O |
|
R |
R. Это запишется так: |
|
|||
|
|
|
|
|
(4.1) |
||
|
|
|
|
||||
|
|
|
|
F1F2Fn R1Fn |
R , |
||
|
Fn |
|
|
|
|
|
|
|
|
|
где |
знак эквивалентности систем |
|||
|
Рис.51 |
|
|||||
|
|
сил. |
|
|
|
||
Следовательно, |
R1 F1 F2; |
R R1 Fn F1 F2 Fn. |
|
||||
В результате этого преобразования первоначальную систему сходя-
щихся сил заменили одной силой R, которая приложена в точке O и совпадает по модулю и направлению с главным вектором системы сил, т.е.
R F1 F2 Fn. |
(4.2) |
Докажем, используя теорему об эквивалентности, что сила R эквива-
лентна первоначальной системе сил, состоящей из силF1,F2,Fn. Главные векторы их равны, как было уже рассмотрено. Главные моменты относи-
тельно полюса O равны нулю. Следовательно, сила R эквивалентна сис-
теме сил F1,F2,Fn, что и требовалось доказать.
Система параллельных сил, направленных в одну сторону, приводится к равнодействующей
A
F1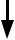
Систему, состоящую из двух параллельных сил, переносом сил по
C |
B |
линии их действия всегда можно |
|||
|
|
|
заменить системой, показанной на |
||
|
|
|
|||
|
|
|
F2 |
рис.52 |
|
|
|
|
Первоначальная система сил |
||
R |
|
|
|
F F |
показана на рис.52. Дока- |
|
|
|
|
1 2 |
|
|
|
|
|
||
|
жем, что сила R, найденная, при- |
|
Рис.52 |
веденным ниже способом, является |
|
равнодействующей этой системы. |
||
|
48
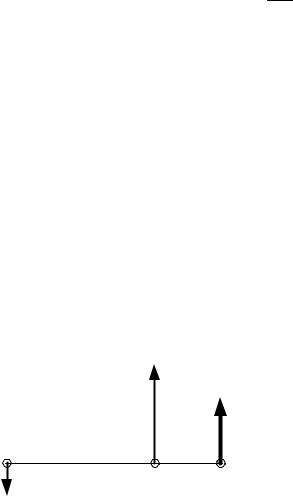
Модуль силы R равен сумме модулей сил системы: |
|
R F1 F2. |
(4.3) |
Линия действия силыR параллельна силам системы и делит расстояние между силами на части, обратно пропорциональные модулям сил:
AC |
|
F2 |
. |
(4.4) |
|
BC |
F |
||||
|
|
|
|||
|
|
1 |
|
|
Для доказательства сравним главные моменты относительно полюса C
первоначальной системы сил и силы R.
Вычислим главный момент первоначальной системы:
F Mc F1 AC F2 BC F1 AC F2 AC F1 0.
2
Равенство нулю момента силы относительно полюса C силы R очевидно.
Главный вектор первоначальной системы равен силе, т.е. F1 F2 R.
Следовательно, R F1,F2 , поэтому R является равнодействующей.
Итак, две параллельные силы, направленные в одну сторону, приводятся к равнодействующей, модуль которой равен сумме модулей сил. Направлена равнодействующая в ту же сторону, что и силы, по прямой, параллельной линиям действия сил. Линия действия равнодействующей делит расстояние между силами на части, обратно пропорциональные модулям сил.
Система параллельных сил, направленных в разные стороны, но не равных по модулю, приводится к равнодействующей
|
F2 |
R |
|
|
|
A |
|
C |
F1 |
|
|
|
B |
Рис.53
Первоначальная система сил F1F2 приведена к виду, показанному на
рис. 53. Требуется доказать, что силаR, равная по модулю
49
R F2 F1, |
(4.5) |
и направленная в сторону большей из сил, параллельная им и приложенная
вточке C, является равнодействующей этой системы, т.е. R F1F2 .
Положение точки приложения равнодействующей определяется из условия, что
BC |
F1 AB |
. |
(4.6) |
|
|
||||
|
F F |
|
||
|
2 |
1 |
|
|
Найдем главный вектор системы сил F F |
. Для этого геометрически |
|||
|
|
1 2 |
|
|
сложим силы: F1 F2 R.
Таким образом, первое условие эквивалентности систем (равенство главных векторов) выполнено. Сравним главные моменты относительно полюса Cпервоначальной и приведенной систем сил.
M |
c |
F AC F BC F AC F |
F1 AB |
|
||||||||||||||||
F F |
||||||||||||||||||||
|
|
|
1 |
|
2 |
|
|
|
1 |
|
|
|
2 |
|
||||||
|
|
|
|
|
|
|
|
F1 AB |
|
|
|
|
|
2 |
1 |
|
||||
F AB BC F |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
1 |
|
|
|
2 F F |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
|
|
|
||
F AB F |
F1 |
AB |
F |
F1 AB |
|
|
|
|
||||||||||||
F F |
F F |
|
|
|
||||||||||||||||
|
|
1 |
|
|
1 |
|
|
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
1 |
2 |
|
|
|
|
2 |
1 |
|
|
|
|
|||
|
F |
|
|
|
|
|
|
2 |
AB F F AB |
|
|
|||||||||
|
AB F F |
F |
|
|
|
|||||||||||||||
|
|
1 |
|
|
2 |
1 |
|
1 |
|
|
|
|
2 1 |
|
|
|
||||
|
|
|
|
|
|
F2 F1 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
AB F F F2 F2 |
F F |
0. |
|
|
|
|
||||||||||||||
|
|
|
|
1 |
2 |
1 |
1 |
|
|
1 |
2 |
|
|
|
|
|
|
|||
Mc R 0.
Следовательно, равны относительно произвольно взятого полюса и главные моменты.
Таким образом, две силы, параллельные между собой, направленные в разные стороны и не равные по модулю, приводятся к равнодействующей, которая равна по модулю разности модулей сил; направлена равнодействующая в сторону большей по модулю силы. Линия действия равнодействующей параллельна линиям действия сил и делит расстояние между силами внешним образом на части, обратно пропорциональные силам.
50

Приведение системы, состоящей из двух параллельных сил, направленных в разные стороны, равных по модулю, если силы не направлены по одной прямой
Две параллельные силы, приложенные к одному твердому телу, равные
по модулю и противоположно направленные, если |
линии действия сил не |
||
совпадают, называются парой сил. |
|
|
|
Пара сил показана на рис.54. Сообщает пара |
|
h |
|
сил телу вращательное движение, т.к. нет воз- |
F1 |
F2 |
|
можности найти одну силу (эквивалентную паре |
|
||
сил), которая сообщила бы телу вращение, то |
|
|
|
пара сил не имеет равнодействующую. Пара сил |
|
|
|
является простейшим видом системы сил. |
Рис.54 |
|
|
Пара сил характеризуется: |
|
плоскостью действия;
количественной мерой пары сил является момент. Момент пары сил равен взятому со знаком плюс или минус произведению модуля одной из сил пары на плечо. Плечом пары называется кратчайшее расстояние между линиями действия сил. Знак момента учитывает направление вращения пары, так же как и момент силы относительно полюса;
главный вектор пары сил равен нулю R F1 F2 0
главный момент пары сил не зависит от положения полюса (рис
|
55). |
F r |
F r |
|
|
|
|
||
M r |
F r |
F |
A |
h |
|
||||
o |
|
1 |
1 2 |
2 1 |
1 2 |
1 |
|
F2 |
|
r |
r |
F AB F. |
|
F1 |
|
|
|||
1 |
2 |
1 |
1 |
|
|
r1 |
|
B |
|
Следовательно, главный момент пары сил |
|
||||||||
|
|
||||||||
равен: |
|
|
|
|
|
|
r2 |
||
M BA F1 |
|
|
(4.7) |
|
|
||||
|
|
|
|
|
|||||
с учетом равенства нулю главного вектора пары сил условием эквивалентности двух пар сил является равенство их главных моментов.
Из условия эквивалентности вытекают следующие свойства пары
сил:
1.Механическое состояние тела не изменится, если пару сил перенести в плоскости ее действия или в параллельную плоскость.
2.Можно изменить модуль сил пары и соответственно плечо пары сил, оставляя при этом неизменным знак и значение момента пары сил.
51
