
2140
.pdf
тела, т.е. выполнять свою роль. На схемах это изображается так, как показано на рис.24 и 25.
RB
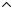 B
B
90
RA
 90
90
A
RC |
R |
Касательная |
C |
D D |
Касательная
Рис.24 Рис.25
2. Подвижный шарнир. Такой связью является катковая опора. Такая связь допускает перемещение тела по неподвижной поверхности, на
|
|
RA |
R |
|
|
|
|
|
которую установлены катки. При |
|
|
|
|
|
|
|
|
этом отрыв катков от поверхности |
|||
|
|
B |
|
|
|
|
|
невозможен, так как в этом случае |
||
|
|
|
|
B |
катки роль связи утрачивают. Ре- |
|||||
|
|
|
|
акция подвижного шарнира на- |
||||||
|
|
A |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
правлена по перпендикуляру к |
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
поверхности, на которую установ- |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Рис.26 |
|
|
|
|
|
лены катки, от поверхности. |
На |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
схемах подвижный шарнир |
изо- |
|
|
|
|
|
|
|
|
|
|
||
бражается так, как показана связь в точках AиB на рис.26.
3. Неподвижный цилиндрический шарнир. Такого рода связью яв-
ляются подшипники скольжения и радиальные подшипники качения. Связь допускает поворот тела относи-
|
|
|
тельно оси подшипника, но препятст- |
|
R |
|
вует любому другому перемещению |
|
Касательная |
тела. Конструктивное исполнение |
|
|
AA |
Тело, на которое |
связи показано на рис.27. Направле- |
|
|
||
Связь |
R |
наложена связь |
ние реакции связи зависит от положе- |
|
Рис.27 |
|
ния точки A, т.е. в большинстве слу- |
|
|
чаев направление неизвестно. Поэто- |
|
|
|
|
му реакцию неподвижного шарнира показывают составляющими, направленными по осям координат. Направление осей координат выбирается заранее. Если шарнир цилиндрический, т.е. рассматриваемое тело имеет цилиндрическую выемку, а связь представляет собой неподвижную ось, как
32
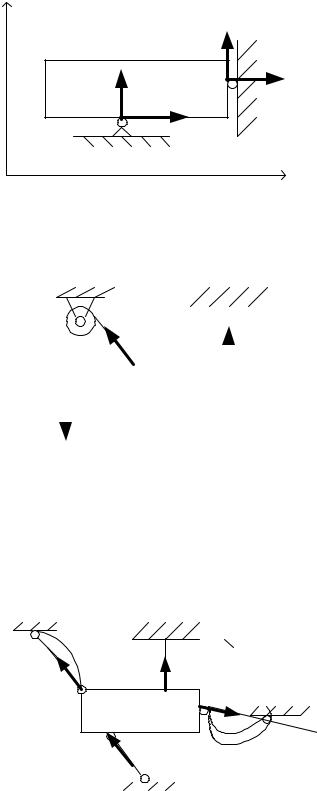
показано на рис.27, то составляющих цилиндрического шарнира две. На |
||||||||||
схемах это изображается так, как показано на рис.28. |
|
|
||||||||
4. |
Неподвижный |
шаровой |
y |
|
YB |
|
|
|||
(сферический) |
шарнир. |
Такая |
|
|
|
|
||||
связь отличается от цилиндриче- |
|
|
|
|
||||||
|
|
|
|
|
||||||
ского шарнира тем, что тело име- |
Y |
|
B |
X |
|
|||||
ет вместо цилиндрической выем- |
A |
B |
||||||||
ки выемку сферической формы, а |
|
XA |
|
|||||||
A |
|
|
||||||||
сама |
связь |
представляет |
собой |
|
|
|
|
|
||
шар, помещенный в эту сфериче- |
|
|
|
|
|
|||||
скую выемку. Реакция шарового |
|
|
|
x |
|
|||||
шарнира раскладывается по трем |
|
|
Рис.28 |
|
|
|||||
осям координат. Изображение на |
|
|
|
|
||||||
схемах такое же, как и цилиндрического шарнира, но встречается в том |
||||||||||
случае, когда силы, действующие на тело, не лежат в одной плоскости. |
|
|
||||||||
5. Веревка, нить, канат, трос и т.д. |
|
|
|
|
||||||
Такая связь называется гибкой свя- |
|
|
|
|
||||||
зью. Тело, которое закреплено с по- |
D |
|
|
|
||||||
мощью |
гибкой |
связи, действует |
на |
|
|
|
T |
A |
|
TB |
|
|
|
|
|||||||
связь с |
силой, |
растягивающей её. |
В |
|
|
|
A |
|
||
|
|
|
|
B |
||||||
противном случае нить свою роль как |
C |
|
|
|
|
|||||
|
|
|
|
|
|
|||||
связь потеряет. Учитывая это, а также |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|||||
то, что сила противодействия со сто- |
|
|
|
P |
|
|
|
|||
|
|
|
|
|
|
|||||
роны связи должна иметь противопо- |
|
|
|
|
|
|
|
|||
ложное направление, реакция гибкой |
Рис.29 |
|
связи направлена по связи от тела, на которое эта связь наложена. На схемах это изображается так, как показано на рис. 29. В точках A и B тело подвешено на тросе (гибкая связь). Кроме того, трос от точки A переброшен через блок с неподвижной осью. К другому концу троса подвешен груз веса P. В этом случае к рассматриваемому телу приложены реакции
TB; TA P.
6. Жесткий стержень, неве- |
|
|
|
сомый и не нагруженный по |
SA |
SB |
|
своей длине, на концах стер- |
SD |
||
жень закреплен шарнирами. В |
A |
B |
|
этом случае стержень находится в |
|
C |
D |
|
|
||
равновесии под действием сил, |
|
SC |
|
приложенных на концах стержня. |
|
|
Очевидно, что силы должны быть |
|
|
|
|
|
|
|
направлены в разные стороны, |
|
Рис.30 |
|
должны быть равны по модулю и |
|
||
|
|
|
|
|
33 |
|
|
линии действия их должны совпадать, т. е. направлены по оси стержня. Только в этом случае их векторная сумма равна нулю. Они могут растягивать или сжимать стержень в зависимости от их направления. Реакция
стержня направлена так, что ее линия действия проходит через оси шарниров, находящихся на концах стержня, от тела, на которое связь наложена, если стержень растянут, и соответственно к телу, если стержень сжат. В точках A,B,C,D связями являются стержни. Сжат стержень или растянут не всегда очевидно, поэтому направление реакции стержня только предположительное и уточняется в результате решения задачи.
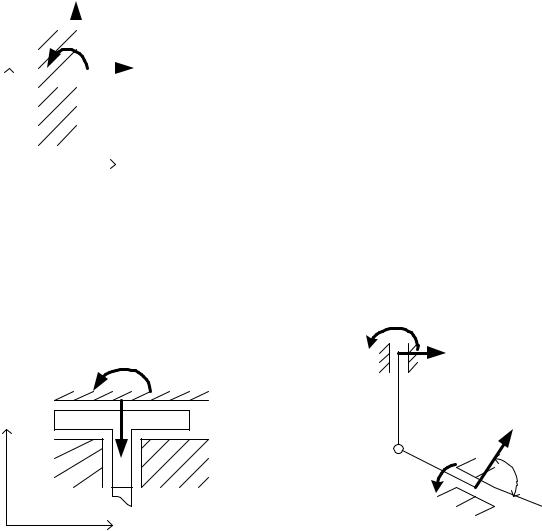
7. Жесткая заделка. Такая связь наложена на тело, если часть тела замурована. Жесткая заделка исключает любое перемещение тела, включая и поворот тела. Объяснение реакций такой связи более подробно будет изложено ниже. Однако изображение жесткой заделки и направление ее реакций без дополнительных разъяс-
|
|
|
YA |
нений показана на рис.31: |
||||
y |
|
|
|
XA |
YA,XA составляющие реакции; |
|||
mA |
|
|||||||
|
mA реактивный момент. Направляет- |
|||||||
|
|
|
|
|
|
|||
|
|
|
|
|
A |
ся он или против направления вращения |
||
|
|
|
|
|
|
|
|
часовой стрелки, или по вращению. |
|
|
|
|
|
|
|
x |
Правильное направление выясняется |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
при решении задачи. Таким образом, ре- |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Рис.31 |
акция жесткой заделки включает три ве- |
||
|
|
|
|
|
личины. |
|||
|
|
|
|
|
|
|
|
|
|
|
8. |
Скользящая заделка. Отличается от жесткой заделки тем, что |
|||||
связь отсутствует в одном из направлений. Если жетко закрепленное тело освободить от связи в одном направлении (например, в горизонтальном), то не будет и составляющей реакции в этом направ-
|
mA |
mA |
A |
RA |
|
A |
|
|
|
y |
RA |
|
C |
RB |
|
|
|||
|
|
|
||
|
|
|
|
900 |
|
|
|
|
B |
|
x |
|
|
mB |
|
Рис.32 |
|
|
Рис.33 |
34
лении. Скользящая заделка на схемах иображается так, как показано на |
||||
рис.32. |
|
|
|
|
На рис.33 показана механическая система, состоящая из двух стерж- |
||||
ней, соединенных шарниром. Связь на эту систему из двух тел наложена |
||||
в точке A скользящая заделка и в точке Bсвязью является также сколь- |
||||
зящая заделка, расположенная иначе, чем в точке A. |
|
|||
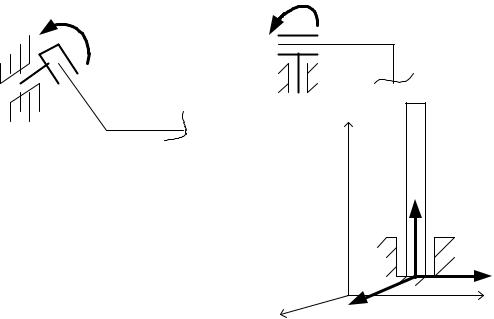
9. Свободная заделка. Если связь «жесткая заделка» преобразовать |
||||
так, что она будет допускать поступательное перемещение тела, а препят- |
||||
ствовать только повороту тела, то получим новую связь, которую назовем |
||||
свободной заделкой (рис.34,35). Очевидно, что из трех реакций жесткой |
||||
заделки, останется только реактивный момент. |
mA |
|
||
|
mA |
|
|
|
|
A |
|
|
|
|
A |
|
|
|
|
|
|
B |
|
|
B |
|
z |
|
|
Рис.35 |
|
||
|
Рис.34 |
|
|
ZA |
10. Подпятник (рис.36). Примером та- |
|
|
||
кой связи является упорный подшипник. |
|
|
|
|
Эту связь можно представить как соедине- |
|
|
YA |
|
ние цилиндрического шарнира с опорной |
|
A |
||
поверхностью. Так же, как и сферический |
|
y |
||
x |
XA |
|
||
шарнир, |
связь такого рода допускает по- |
|
||
ворот тела, препятствуя при этом поступа- |
|
|
|
|
тельному перемещению тела в любом на- |
|
Рис.36 |
|
|
правлении. Реакция, как и сферического |
|
|
|
|
шарнира, состоит из трех составляющих, направленных по предварительно |
||||
выбранным осям координат. |
|
|
|
|
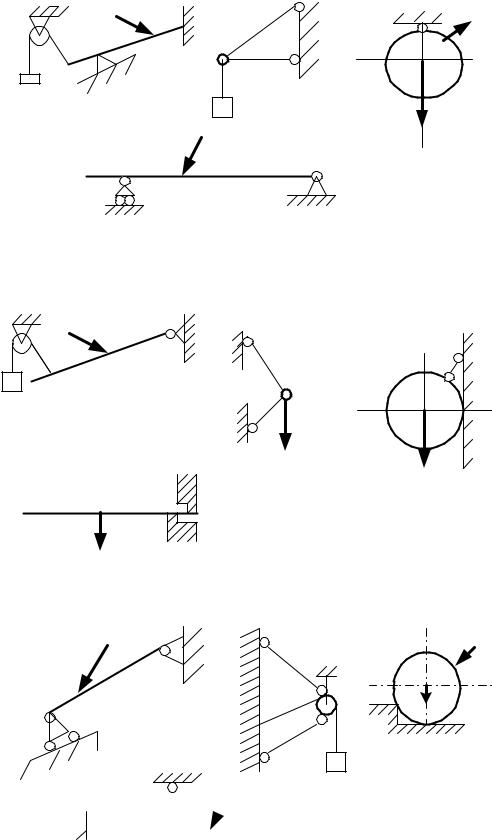
Выполните для самоконтроля задание № 5
В представленных схемах назовите каждую связь и покажите ее реакцию. Связи наложены на балку AB(схема a); узел C(схемаb); шар
(схема c); стержень MN (схема d).
35
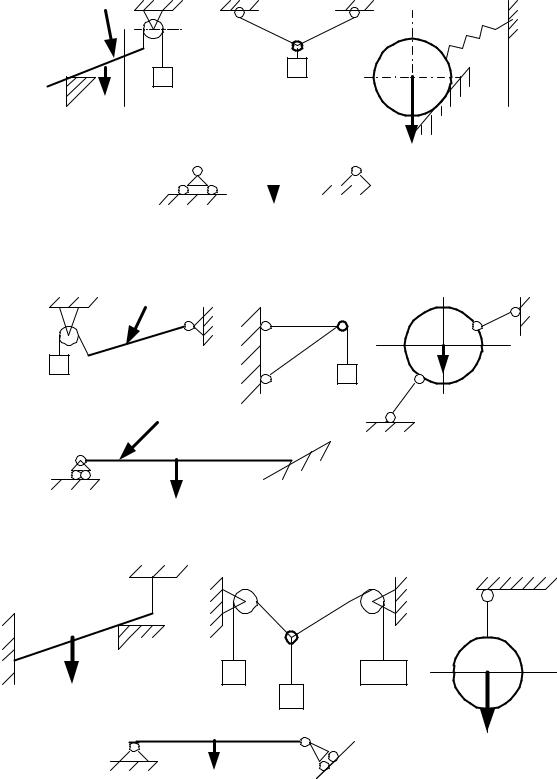
Рисунки к заданию № 5
1.
a) |
b) |
C |
c) |
|
B |
|
D |
A |
|
|
|
|
|
|
d) M |
N |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.37 |
|
2. |
b) |
C |
c) |
B |
|||
a) |
|
|
D |
|
|
|
|
A |
|
|
|
d) M |
N |
|
|
Рис.38 |
3. |
|
|
a) |
B b) |
c) |
|
|
C |
A |
|
D |
d) M N
Рис.39
36
4. |
|
b) |
c) |
a) |
B |
||
|
A |
C |
D |
|
|
||
|
d) |
|
|
N
M
Рис.40
5. |
B |
c) |
|
a) |
b) |
||
|
|||
|
|
||
A |
C |
D |
d) |
|
M |
N |
|
|
|
Рис.41 |
6. |
B |
b) |
a) |
|
c) |
|
|
D |
A |
|
C |
|
|
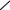 M
M 
 d)
d) 
 N
N
Рис.42
37
7. |
B b) |
|
c) |
a) |
C |
||
|
|
D |
|
|
|
|
 A
A
d) 
M N
N
Рис.43
8. |
|
b) |
|
|
a) |
B |
C |
||
|
||||
A |
|
|
|
|
M |
N |
c) |
D |
|
|
|
|
d)
Рис.44
Вопросы по теме 2 для самоконтроля
1.Что называется связью?
2.Какое тело называется свободным?
3.Какие силы называются реакциями; активными силами?
4.Как читается принцип «освобождаемости» твердого тела от связей?
5.Перечислите все типы связей.
6.Как направлена реакция гибкой связи?
7.Как направлена реакция, если связью является гладкая поверхность, линия или опорная точка?
8.Какие шарнирные опоры осуществляют связь и как изображать на схемах реакции этих опор?
38
9.Как направлена реакция прямолинейного ненагруженного и невесомого стержня, соединенного с твердым телом и опорной поверхностью шарнирами?
10.Если твердое тело соединено с опорой при помощи стержня, имеющего на концах шарниры, и если вес стержня учитывается, как показать реакцию опорного шарнира?
11.Сколько и какие неизвестные величины определяются при нахождении реакции жесткой заделки?
12.Чем скользящая заделка отличается от жесткой связи и какие неизвестные величины определяются при нахождении реакции скользящей заделки?
13.Какому перемещению тела препятствует свободная заделка и какая величина называется реакцией свободной заделки?
14.Как сформулирована аксиома о равенстве действия и противодействия?
15.Правильно ли на приведенном рисунке показана реакция неподвижного шарнира?
16.Какая связь изображена на рисунке?
17.Если тело подвешено на канате, как направлена сила, с которой это тело действует на канат?
39
Тема 3
СИСТЕМА СИЛ
Все силы, приложенные к одному твердому телу, образуют систему сил. Если линии действия всех сил системы лежат в одной плоскости, то эти силы образуют плоскую систему сил. В случае, если линии действия сил системы не лежат в одной плоскости, система сил называется пространст-
венной.
Каждая из этих систем может быть либо системой сходящихся сил, либо системой параллельных сил, либо произвольной системой.
Если линии действия всех сил системы пересекаются в одной точке, то силы образуют систему сходящихся сил.
Если линии действия всех сил системы параллельны между собой, то такая система называется системой параллельных сил.
Если систему сил нельзя отнести ни к системе сходящихся, ни к системе параллельных сил, то система сил является пространственной или плоской системой произвольно расположенных сил.
1. Способы сложения сил
Графический способ сложения сил заключается в построении сило-
вого многоугольника. На рис. 45 показано графическое сложение сил
F3
F1 F2
A
F1
O F2
R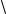 C F3
C F3  B
B
Рис.45
F1 F2 F3. Точка O, от которой на-
чинается построение векторного многоугольника, выбирается произвольно. От точки O откладывается вектор
OA, равный векторуF1. От точки A
откладывается вектор AB равный
вектору F2. Так можно сложить лю-
бое количество векторов, совмещая при построении конец предыдущего вектора слагаемого с началом последующего. Замыкает многоугольник
вектор OC, равный по модулю и направлению сумме векторов F1 F2 F3,
т.е. R. Таким образом, F1 F2 F3 R.
40

Аналитический способ сложения сил заключается в предваритель- |
||||||||||||
ном вычислении проекций на оси координат вектора суммы R. |
|
|
|
|||||||||
Каждый вектор равенства F1 F2 F3 |
R, |
по формуле разложения |
||||||||||
вектора по осям координат, можно представить: |
|
|
|
|
||||||||
|
|
|
|
F1 iF1x jF1y kF1z ; |
|
|
|
|||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
F2 iF2x jF2y kF2z ; |
|
|
|
|||||
|
|
|
|
F3 iF3x jF3y kF3z; |
|
|
|
|||||
|
|
|
|
|
R iRx jRy kRz. |
|
|
|
||||
Подставив эти значения в исходную формулу, получим |
|
|
|
|||||||||
iRx jRy kRz i (F1x F2x F3x)+ j (F1y F2y F3y)+ |
|
|
||||||||||
+k (F1z F2z F3z). |
|
|
|
|
|
(3.1) |
|
|||||
Учитывая, чтобы левая и правая части уравнения были равны, должны |
||||||||||||
быть равны скалярные коэффици- |
|
|
|
z |
|
|
|
|||||
енты при одинаковых ортах, т.е.: |
|
|
|
|
|
|
||||||
R |
x |
(F |
F |
F |
); |
|
|
|
Rz |
|
|
|
|
1x |
2x |
3x |
|
|
|
|
|
|
|
|
|
Ry (F1y F2y F3y); |
|
|
|
R |
|
|
|
|||||
Rz (F1z F2z |
F3z). |
|
|
k |
|
R |
|
|
||||
R |
|
|
|
y |
y |
|||||||
|
|
|
|
|
|
|
|
|||||
На рис.46 показаны проекции |
|
x |
j |
|
|
|
||||||
|
|
i |
|
|
|
|
||||||
вектор-суммы на оси координат: |
x |
|
|
|
|
|
|
|||||
Rx,Ry,Rz . Учитывая, что они яв- |
|
|
|
Рис.46 |
|
|
|
|||||
|
|
|
|
|
|
|
||||||
ляются сторонами параллелепипеда, то диагональ параллелепипеда равна
R |
Rx2 Ry2 Rz2 . |
(3.2) |
|
41 |
|
