
2140
.pdf
P |
P |
|
|
|
b |
|
, |
P |
P |
|
a |
|
, |
P |
0; |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
2x |
|
2 |
|
|
a2 b2 |
|
2y |
2 |
|
a2 |
b2 |
|
2z |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
x3 0, |
|
y3 a, |
|
z3 0; |
|
|
|
|
|
|
|
|||||||||||||
P |
0, |
P |
|
|
a |
|
, |
P |
|
|
c |
|
. |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
3x |
|
|
|
|
|
3y |
|
|
|
|
|
|
a2 c2 |
|
3z |
|
|
|
|
a2 c2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
x4 b, |
|
y4 a, |
z4 c; |
|
|
|
|
|
|
|
||||||||||||||||
P |
P |
|
|
b |
|
, |
P |
0, |
P |
P |
|
c |
|
. |
|||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
4x |
|
4 |
|
|
b2 c2 |
|
|
|
|
|
|
4y |
|
|
|
|
4z |
4 |
|
b2 c2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Моменты сил относительно координатных осей равны:
|
|
|
|
|
m |
x(P1) |
P |
a |
; m |
y(P1) |
P |
b |
; m |
z(P1) |
0. |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 2 |
|
|
1 2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
m |
x(P ) |
P |
|
|
|
|
a |
|
c; m |
y(P ) |
P |
|
|
|
|
b |
|
|
|
c; |
m |
z(P |
) |
|
0. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
2 |
|
|
a2 b2 |
|
|
|
2 |
|
|
|
a2 b2 |
|
|
|
|
|
|
||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||||||||
|
|
|
m |
|
|
|
P |
|
|
|
|
|
c |
|
|
a; |
m |
|
|
|
|
0; |
|
m |
|
|
|
0. |
|
|
|
|||||||||
|
|
|
x(P ) |
|
|
|
|
|
|
|
|
y(P |
) |
|
|
z(P ) |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
3 |
|
|
a2 c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
||||||||
|
m |
x(P |
) |
P |
|
|
|
|
c |
|
a; m |
y(P ) |
0; m |
z(P ) |
P |
|
b |
|
|
a. |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
4 |
|
|
|
b2 c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
b2 c |
|
|
|
||||||||||||||
|
|
4 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
2 |
|
|
|||||||||||
Вариант 4 (рис.18)
Координаты точек приложения сил и проекции сил на оси координат равны:
x1 b, |
y1 a, |
z1 c; |
P1x 0, |
P1y 0, P1z P1. |
|
|
22 |
|
|
|
|
|
|
|
|
|
x2 b, |
y2 a, |
z2 0; |
|
|
|
|
|
|
|
||||||||||||||||
P |
P |
|
|
|
|
|
b |
|
, |
|
|
P |
0, |
P |
P |
|
|
c |
|
. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
2x |
|
2 |
|
|
|
c2 b2 |
2y |
|
|
|
2z |
2 |
|
c2 b2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
x3 0, |
y3 a, |
z3 0; |
|
|
|
|
|
|
|
||||||||||||||||
P |
|
P |
|
|
|
|
b |
|
, |
P |
|
P |
|
a |
|
, P |
0. |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
3x |
3 |
|
|
|
a2 b2 |
3y |
3 |
|
a2 |
b2 |
|
3z |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
x4 0, |
y4 a, |
z4 c; |
|
|
|
|
|
|
|
||||||||||||||||
P4x P4 |
|
|
|
b |
|
|
|
, P4y |
P4 |
|
|
|
|
|
|
a |
|
|
, |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
a2 b2 c2 |
|
c |
|
|
|
a2 b2 c2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
P4z P4 |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 b2 c2 |
|
|
|
|
|
|
|
||||||||
Моменты сил относительно координатных осей равны:
|
|
mx(P ) P1a; |
my(P ) P1b; |
|
|
mz(P ) 0. |
||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||
m |
x(P2) |
P |
|
|
c |
|
|
a; m |
y(P2) |
|
P |
|
|
c |
|
b; |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
2 |
|
b2 c2 |
|
|
|
|
|
2 |
|
|
b2 c2 |
||||||||||||||
|
|
|
|
m |
z(P2) |
P |
|
|
|
|
b |
|
|
|
a. |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
2 |
|
b2 c2 |
|
|
|
|
|
|
|
|||||||||||
m |
x(P ) |
0; m |
y(P ) |
0; m |
z(P ) |
P |
|
|
|
b |
|
a. |
||||||||||||||
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
a2 b2 |
|||||||||||
|
|
3 |
|
|
|
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
||||||
23
mx(P ) |
0; my(P ) P4 |
|
c |
|
|
b; |
||||
|
|
|
|
|
|
|||||
|
|
|
|
|
||||||
4 |
4 |
|
|
|
a2 b2 c2 |
|||||
|
mz(P4) P4 |
|
|
a |
b. |
|||||
|
|
|
|
|
|
|
||||
|
a2 b2 c2 |
|||||||||
Вариант 5 (рис.19)
Координаты точек приложения сил и проекции сил на оси координат равны:
|
|
|
|
|
|
|
x1 b, |
y1 a, |
z1 c; |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
P1x 0, |
P1y 0, P1z P1. |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
x2 0, |
y2 0, |
z2 c; |
|
|
|
|
|
|
|
||||||||||||||||||
P |
|
P |
|
|
|
|
b |
|
|
, |
P |
P |
|
|
a |
|
, P |
0. |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
2x |
2 |
|
|
|
a2 b2 |
|
2y |
2 |
|
a2 |
b2 |
|
2z |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
x3 0, |
y3 a, |
z3 c; |
|
|
|
|
|
|
|
||||||||||||||||||
P |
P |
|
|
|
b |
|
|
, |
P |
0, |
|
P |
P |
|
c |
|
. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
3x |
|
3 |
|
|
|
|
c2 b |
2 |
|
|
|
|
3y |
|
|
|
3z |
3 |
c2 b2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
x4 b, |
y4 a, |
|
z4 0; |
|
|
|
|
|
|
|
|||||||||||||||||
P4x P4 |
|
|
b |
|
|
|
|
|
|
|
, P4y P4 |
|
|
|
|
|
|
|
a |
|
|
, |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
a2 b2 c2 |
c |
|
|
|
|
a2 b2 c2 |
|||||||||||||||||||||
|
|
|
|
|
|
|
P4z P4 |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 b2 c2 |
|
|
|
|
|
|
|
|||||||||||
Моменты сил относительно координатных осей равны:
mx(P ) P1a; |
my(P ) P1b; |
mz(P ) 0. |
1 |
1 |
1 |
|
24 |
|

m |
x(P ) |
P |
|
|
a |
|
c; m |
y(P ) |
P |
|
|
|
b |
|
|
|
|
c; m |
z(P |
) |
0. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
2 |
|
b2 a2 |
|
|
|
|
|
2 |
|
|
|
b2 a2 |
|
|
|
|
|
|||||||||||||||||||
|
2 |
|
|
|
c |
|
|
2 |
|
|
|
|
|
|
|
|
|
b |
|
|
2 |
|
|
|
||||||||||||||
|
|
m |
x(P3) |
P |
|
|
|
|
|
|
|
|
a; |
|
|
m |
y(P3) |
|
P |
|
|
|
|
|
c; |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
3 |
|
|
|
b2 c2 |
|
|
|
3 |
|
|
|
b2 c2 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
m |
z(P3) |
|
P |
|
|
|
b |
|
|
a. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
c2 b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
mx(P4) P4 |
|
|
|
a |
|
|
c; |
my(P4) P4 |
|
|
|
|
|
b |
|
|
c; |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
a2 b2 c2 |
|
|
a2 b2 c2 |
||||||||||||||||||||||||||||||||
mz(P4) 0.
Вариант 6 (рис.20)
Координаты точек приложения сил и проекции сил на оси координат равны:
x1 0, |
y1 a, z1 0; |
P1x 0, |
P1y 0, P1z P1. |
x2 b, y2 a, z2 0;
P |
0, P |
P |
|
|
|
a |
|
, |
P |
P |
|
|
c |
|
. |
||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
2x |
|
2y |
2 |
|
|
|
a2 c2 |
|
2z |
2 |
|
|
a2 c2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
x3 b, |
y3 a, |
z3 c; |
|
|
|
|
|
|
|||||||||||||
P |
P |
|
|
b |
|
, |
P |
P |
|
|
|
a |
|
, P |
0. |
||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
3x |
3 |
|
a |
2 b2 |
3y |
3 |
|
a2 b2 |
|
|
3z |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
x4 b,. |
y4 0, |
z4 c; |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P4x P4 |
|
b |
|
|
|
, P4y P4 |
|
|
a |
|
, |
||
|
|
|
|
|
|
|
|
|
|||||
|
a2 b2 c |
2 |
|
|
|
a2 b2 c2 |
|||||||
|
|
|
|
c |
|
|
|
|
|||||
|
|
P4z P4 |
|
|
|
|
. |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
a2 b2 c2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Моменты сил относительно координатных осей равны:
|
|
|
|
|
mx(P ) P1a; |
|
|
my(P ) 0; |
mz(P ) 0. |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||
|
|
m |
x(P2) |
P |
|
|
|
|
c |
|
|
a; |
|
|
m |
y(P2) |
P |
|
|
|
|
c |
|
|
|
b; |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
2 |
|
c2 a2 |
|
|
|
|
|
|
|
2 |
|
|
a2 c2 |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
m |
z(P2) |
P |
|
|
|
|
|
a |
|
|
b. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
a2 c2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
m |
x(P |
) |
P |
|
|
a |
|
c; m |
y(P |
) |
P |
|
|
|
|
b |
|
c; |
|
m |
z(P ) |
0. |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
3 |
|
|
b2 a2 |
|
|
|
|
|
|
|
3 |
|
|
b2 a2 |
|
|
|
|
|
|||||||||||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
||||||||||||||||
|
|
|
|
|
|
|
mx(P ) P4 |
|
|
|
|
|
|
a |
|
|
|
|
c; |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
a2 b2 c2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
my(P ) 0; |
|
mz(P ) P4 |
|
|
|
|
|
a |
|
|
|
|
|
|
b. |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
a2 b2 c2 |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
4 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Вариант 7 (рис.21)
Координаты точек приложения сил и проекции сил на оси координат
равны: |
|
|
|
x1 b, |
y1 0, |
z1 0; |
|
P1x 0, |
P1y 0, |
P1z P1. |
|
26
x2 b, y2 a, z2 c;
P |
0, P |
|
P |
|
|
|
a |
|
, |
P |
P |
|
c |
|
|
|
|
. |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
2x |
|
2y |
2 |
|
|
|
a2 c2 |
|
2z |
2 |
|
|
|
a2 c2 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
x3 0, |
y3 a, |
z3 c; |
|
|
|
|
|
|
|
|||||||||||||||||||
P |
|
P |
|
|
|
b |
|
, |
P |
P |
|
|
|
a |
|
, P |
0. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
3x |
3 |
|
|
a2 b2 |
|
3y |
|
|
|
3 |
|
a2 b2 |
|
3z |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
x4 b, |
y4 0, |
z4 c; |
|
|
|
|
|
|
|
|||||||||||||||||||
|
P4x P4 |
|
|
b |
|
|
|
, P4y |
P4 |
|
|
|
|
|
|
|
a |
|
|
, |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
a2 b2 c2 |
|
|
c |
|
|
|
|
|
|
|
a2 b2 c2 |
|||||||||||||||||
|
|
|
|
|
|
P4z P4 |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 b2 c2 |
|
|
|
|
|
|
|
|||||||||||||
Моменты сил относительно координатных осей равны:
|
|
|
|
mx(P ) 0; my(P ) |
P1b; |
|
mz(P ) 0. |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||
m |
x(P |
) |
0; m |
y(P ) |
P |
|
|
|
|
c |
|
|
|
b; m |
z(P ) |
P |
|
|
|
a |
|
b. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
a2 c2 |
|
|
|
2 |
|
|
|
|
|
||||||||||||||
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
a2 c2 |
|
|
|||||||||
|
|
m |
x(P3) |
P |
|
|
|
a |
|
c; |
|
m |
y(P3) |
P |
|
|
b |
|
c; |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
3 |
|
|
b2 a2 |
|
|
|
|
|
|
3 |
|
|
b2 a2 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
m |
z(P ) |
P |
|
|
|
b |
|
a. |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
a2 b2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
27
|
mx(P4) P4 |
|
a |
|
|
c; |
|
|
||
|
|
|
|
|
|
|
|
|||
|
a2 b2 c2 |
|
|
|||||||
my(P ) |
0; mz(P ) P4 |
|
|
a |
|
b. |
||||
|
|
|
|
|
||||||
a2 b2 c2 |
||||||||||
4 |
4 |
|
|
|
|
|
||||
Вариант 8 (рис.22)
Координаты точек приложения сил и проекции сил на оси координат равны:
|
|
|
|
|
|
x1 0, |
y1 a, |
|
z1 0; |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
P1x 0, |
P1y 0, |
P1z P1. |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
x2 b, |
|
y2 0, |
|
z2 c; |
|
|
|
|
|
|
|
||||||||||||||||||
P |
0, |
P |
P |
|
|
|
|
a |
|
, |
|
|
P |
P |
|
c |
|
. |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
2x |
|
|
|
|
2y |
2 |
|
a2 c2 |
|
|
2z |
2 |
|
a2 c2 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
x3 b, |
y3 a, |
|
z3 c; |
|
|
|
|
|
|
|
||||||||||||||||||||
P |
|
P |
|
|
|
b |
|
, |
P |
P |
|
|
a |
|
, P |
0. |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
3x |
3 |
|
|
a2 b2 |
|
3y |
3 |
|
|
a2 b2 |
|
3z |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
x4 b, |
|
y4 a, |
|
z4 0; |
|
|
|
|
|
|
|
||||||||||||||||||
P4x P4 |
|
|
|
b |
|
|
|
, |
P4y |
|
P4 |
|
|
|
|
|
|
|
a |
|
|
, |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
a2 b2 c2 |
|
|
c |
|
|
|
a2 b2 c2 |
|||||||||||||||||||||
|
|
|
|
|
|
|
P4z P4 |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
a2 b2 c2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
28
Моменты сил относительно координатных осей равны:
|
|
|
|
|
|
mx(P ) P1a; |
|
|
|
my(P ) 0; |
mz(P ) 0. |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
m |
x(P2) |
P |
|
|
|
|
a |
|
|
|
|
|
c; |
m |
y(P2) |
P |
|
|
|
|
|
c |
|
|
b; |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
a2 c2 |
|
|
2 |
|
|
a2 c2 |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
m |
z(P2) |
P |
|
|
|
a |
|
|
b. |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
a2 c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
m |
x(P |
) |
P |
|
|
|
a |
|
c; m |
y(P ) |
P |
|
|
|
b |
|
c; |
m |
z(P ) |
|
0. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
3 |
|
|
b2 a2 |
|
|
|
|
|
|
3 |
|
b2 a2 |
|
|
|
|
|
|||||||||||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
3 |
|
|
||||||||||||||||||
|
mx(P4) P4 |
|
|
c |
|
|
|
a; |
my(P4) P4 |
|
|
|
|
|
c |
|
|
b; |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
a2 b2 c2 |
|
|
|
|
a2 b2 c2 |
|||||||||||||||||||||||||||||||||
mz(P4) 0.
Вопросы по теме 1 для самоконтроля
1.Как читается аксиома параллелограмма сил?
2.Чем отличается составляющая силы от проекции силы на ось?
3.Чему равна проекция силы на ось, если линия действия силы параллельна оси; перпендикулярна оси; составляет угол с осью и этот угол острый; если этот угол тупой?
4.Как определить знак проекции силы на ось?
5.В чем заключается метод двойного проектирования и когда он применяется?
6.Что называется моментом силы относительно полюса?
7.В каком случае момент силы относительно полюса положительный; равен нулю?
8.Как определить по модулю и направлению вектор-момент силы Fотносительно полюса O?
O
 F
F
29
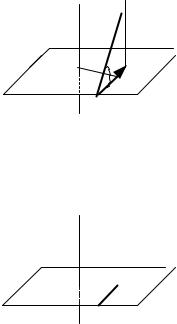
9. Что называется моментом силы F относительно оси z?
z F
F
h
10.Как определить момент силы Fотносительно оси zв случае, когда сила перпендикулярна оси?
z
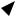 F
F
11. В каких случаях момент силы относительно оси равен нулю?
11.Запишите аналитические формулы для вычисления моментов силы относительно координатных осей?
13.Запишите формулу разложения вектора силы по осям координат.
14. Как направлен вектор-момент относительно полюса силы, лежащей в координатной плоскости xOy, если полюс тоже лежит в этой плоскости?
30
Тема 2
ТИПЫ СВЯЗЕЙ И НАПРАВЛЕНИЯ РЕАКЦИЙ
1. Аксиома равенства действия и противодействия
Всякому действию соответствует равное и противоположно направ-
ленное противодействие. В природе не существует одностороннего действия силы. Всегда друг на друга действуют два тела с силами, направленными по одной прямой в противоположные стороны и равными по модулю.
2. Свободное и несвободное тело. Связи. Реакции связей
Свободным называется тело, перемещение которого в пространстве не ограничено другими телами. Свободным является находящееся в полете тело: брошенный мяч, летящий самолет и т.д.
Несвободным называется тело, перемещению которого в пространстве препятствуют другие тела, называемые связями.
Сила, с которой связь действует на тело, называется реакцией этой связи. Все силы, кроме реакций, будем называть в дальнейшем заданными или активными.
Согласно принципу равенства действия и противодействия, сила, с которой тело действует на связь, равна реакции связи.
3. Принцип «освобождаемости» твердых тел от связей
Любое несвободное тело можно рассматривать как свободное, если, отбросив связи, заменить реакциями их действие на тело. Реакции следует направлять соответствующим образом в зависимости от типа связи.
4. Типы связей и направления реакций
Связь осуществляет:
1.Гладкая поверхность, линия или точечная опора. Рассматривае-
мое тело, показанное на рис. 24 и 25, опирается на гладкую поверхность: прямолинейную или криволинейную (связь в точке A), и ребро двухгранного угла (связь в точке B), на рис.25 опорой является остриё (в точках C;Dсвязью является точечная опора). Реакция направлена по нормали к общей касательной, проведенной к связи и телу, в точках A,B, C,D и
направлена реакция от связи к телу. Последнее объясняется тем, что только в этом случае указанные связи будут препятствовать перемещению
31
