Решение оптимизационной задачи

Все три функционала сводятся к одному виду:

Задача – имея функционалы вида найти функцию, имеющую полюсы только в левой полуплоскости комплексного переменного, которая обеспечивает минимум функционала.

Допустим, такая функция найдена, обозначим ее :

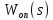Если вместо функции в функционалподставить близкую ей функцию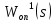, то функционал может только увеличиться:

Раскроем скобки и введем обозначения 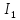и:

По теореме Парсеваля и так как – четная функция:

Тогда, с учетом введенных обозначений выражение примет вид:

Найдем его минимум. Для этого возьмём производную и приравняем ее нулю:

Получаем, что – необходимое и достаточное условие оптимальности системы.

Полученное уравнение (Винера-Хопфа) содержит две неизвестных функции:

– имеет полюсы только в левой полуплоскости.

– имеет полюсы только в правой полуплоскости.

Алгоритм решения уравнения Винера-Хопфа

Факторизация

Сепарация

Пример решения

1. Факторизация

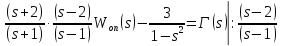
2. Сепарация

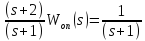
Индикатор совместимости исходных данных в уравнении Винера-Хопфа

В некоторых случаях исходные данные могут быть таковыми, что не существует решений, обеспечивающих конечность величины функционала и, как следствие, его оптимум. Задача состоит в том, чтобы по исходным данным определить существует ли решение, доставляющее функционалу оптимум.

Преобразуем функционал к виду:

Это соотношение имеет место при любых , в том числе и при, но для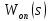значениедолжно быть конечным. Следовательно, исходные данные должны быть такими, чтобы выполнялось неравенство:

Такой интеграл сходиться, если степень числителя меньше степени знаменателя в подынтегральной функции и полюсы на мнимой оси отсутствуют.

Минимальное значение функционала

Оптимальная функция удовлетворяет интегральному уравнению (из которого вытекает уравнение Винера-Хопфа):

Причем удовлетворяет при любых из класса функций, т.е. и при

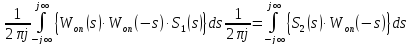
Подставим полученное значение дляв исходный функционал и найдем другое его выражение, которое обычно проще вычисляется:

Математическая модель ограничения на компенсацию нулей и полюсов

Рассмотрим две передаточные функции:

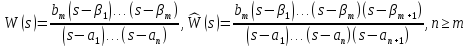
Тогда, если , то и. А также, пусть все полюсы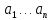расположены в левой полуплоскости.

Рассмотрим, близки ли импульсные переходные функции и:

Рассмотрим -е коэффициенты:

Так как при 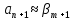значение, то, при. А последние слагаемое.

Выводы:

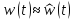, если полюслежит в левой полуплоскости, так как:

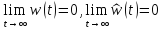
, если полюслежит в правой полуплоскости, так как:

Тогда, в передаточной функции близкие нули и полюсы, лежащие в левой полуплоскости можно сократить, что недопустимо, если они лежат в правой.

Примеры решения оптимизационной задачи

Алгоритм решения

1. Записать функционал

2. По функционалу записать уравнение Винера-Хопфа.

3. Решить уравнение Винера-Хопфа.

4. Определить передаточные функции УУ.

Пример 1

Дано: .

Найти .

Запись функционала.

Так как (1) и (3) части функционала не могут выполняться одновременно, выбрасываем одну из них, например первую.

Запись уравнения Винера-Хопфа

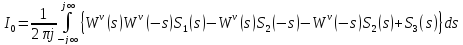
Дальше вообще не понятно как из функционалов получается это самое уравнение…

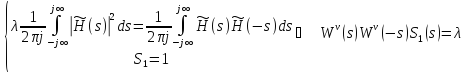
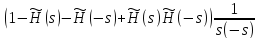
Решение уравнения Винера-Хопфа

1. Факторизация

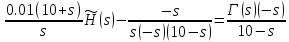
2. Сепарация

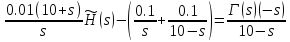
Определение передаточных функций УУ

А в лекциях почему-то без 10ки.

Пример 2

Дано: .

Найти и.

Запись функционала.

Так как функционал 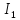совпадает с функционаломиз предыдущей задачи, можно сразу написать, что

Запись и решение уравнения Винера-Хопфа для функционала

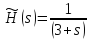
Определение передаточных функций УУ