
TeorUpr
.pdf
|
1 |
Теория управления |
|
Оглавление |
|
Основные понятия........................................................................................................................................................... |
3 |
Принципы управления................................................................................................................................................ |
3 |
Постановка задачи ...................................................................................................................................................... |
4 |
Основа математического обеспечения для решения задач конструирования систем управления ....................... |
4 |
Виды операторов ........................................................................................................................................................ |
4 |
Решение линейных стационарных дифференциальных уравнений .......................................................................... |
4 |
Прямое и обратное преобразования Лапласа ......................................................................................................... |
4 |
Равенство Парсеваля .................................................................................................................................................. |
5 |
Алгоритм решения дифференциального уравнения с использованием преобразования Лапласа ................... |
5 |
Пример решения 1 .................................................................................................................................................. |
6 |
Пример решения 2 .................................................................................................................................................. |
6 |
Переходной процесс и его оценки. ............................................................................................................................... |
7 |
Пример ..................................................................................................................................................................... |
7 |
Импульсная переходная функция ................................................................................................................................. |
8 |
Дельта-функция и ее свойства ....................................................................................................................................... |
8 |
Связь между импульсной переходной функцией и переходным процессом....................................................... |
9 |
Алгебра передаточных функций.................................................................................................................................... |
9 |
Последовательное соединение................................................................................................................................. |
9 |
Параллельное соединение ........................................................................................................................................ |
9 |
Цепь с обратной связью.............................................................................................................................................. |
9 |
Свойства линейных систем............................................................................................................................................. |
9 |
Принцип гомогенности............................................................................................................................................... |
9 |
Принцип суперпозиции ............................................................................................................................................ |
10 |
Принцип наложения ................................................................................................................................................. |
10 |
Система управления одномерным объектом ............................................................................................................ |
11 |
Алгоритмы конструирования множества УУ .............................................................................................................. |
11 |
Возможные структуры управляющего устройства ..................................................................................................... |
12 |
Критерии оценки качества системы и управляющего устройства............................................................................ |
13 |
Алгебраические критерии устойчивости .................................................................................................................... |
13 |
Критерий Гурвица ..................................................................................................................................................... |
13 |
Критерий Льенара–Шипара ..................................................................................................................................... |
14 |
Частотные критерии устойчивости .............................................................................................................................. |
14 |
Амплитудно-фазовая характеристика..................................................................................................................... |
15 |
|
2 |
Свойства частотной характеристики........................................................................................................................ |
15 |
Принцип аргумента....................................................................................................................................................... |
16 |
Критерий Михайлова.................................................................................................................................................... |
16 |
Критерий Найквиста...................................................................................................................................................... |
17 |
Частотные критерии качества ...................................................................................................................................... |
17 |
Интегральная квадратичная оценка качества ............................................................................................................ |
18 |
Желаемые и действительные передаточные функции ............................................................................................. |
18 |
Фильтр Баттерворта (желаемая передаточная функция).......................................................................................... |
19 |
Критерии близости действительных передаточных функций к желаемым ............................................................ |
20 |
Интегральная полулогарифмическая функция чувствительности............................................................................ |
20 |
Алгоритм определения функций чувствительности .............................................................................................. |
21 |
Формулы для численной оценки интегральных функций чувствительности...................................................... |
21 |
Способ 1 ................................................................................................................................................................. |
21 |
Способ 2 ................................................................................................................................................................. |
22 |
Свойство оценки интегральной функции чувствительности................................................................................. |
22 |
Оценка сложности УУ на элементах дискретной техники......................................................................................... |
22 |
Математические модели ограничений....................................................................................................................... |
23 |
Математические модели ограничений на реализуемость ....................................................................................... |
23 |
Ограничения, которым должна удовлетворять математическая модель реального объекта.......................... |
24 |
Ограничения, которым должна удовлетворять математическая модель УУ...................................................... |
24 |
Соотношения, обеспечивающие реализуемость УУ .................................................................................................. |
24 |
I случай ....................................................................................................................................................................... |
24 |
II случай ...................................................................................................................................................................... |
25 |
Математическая модель ограничения на реализуемость в изопериметрической форме.................................... |
26 |
Ограничения на реализуемость как мера качества системы управления............................................................... |
26 |
Корректность задачи..................................................................................................................................................... |
27 |
Математическая модель ограничений на астатизм в системе ................................................................................. |
27 |
Теорема Вейерштрасса............................................................................................................................................. |
27 |
Математическая модель .......................................................................................................................................... |
27 |
Математическая модель ограничения на астатизм в изопериметрической форме .............................................. |
28 |
Ограничения на астатизм как мера качества системы управления ......................................................................... |
28 |
Интегральный квадратичный критерий оценки качества системы.......................................................................... |
29 |
Решение оптимизационной задачи ............................................................................................................................ |
30 |
Алгоритм решения уравнения Винера-Хопфа ............................................................................................................ |
31 |
Факторизация ............................................................................................................................................................ |
31 |
Сепарация .................................................................................................................................................................. |
31 |
Пример решения....................................................................................................................................................... |
32 |

|
3 |
Индикатор совместимости исходных данных в уравнении Винера-Хопфа............................................................. |
32 |
Минимальное значение функционала........................................................................................................................ |
33 |
Математическая модель ограничения на компенсацию нулей и полюсов ............................................................ |
33 |
Примеры решения оптимизационной задачи ........................................................................................................... |
34 |
Алгоритм решения .................................................................................................................................................... |
34 |
Пример 1 .................................................................................................................................................................... |
34 |
Пример 2 .................................................................................................................................................................... |
36 |
Основные понятия
Совокупность взаимосвязанных функциональных элементов, образуют систему управления.
Система должна быть способной реализовывать поставленные цели.
В теории управления функциональный элемент рассматривается как преобразователь входа в переменную выхода.
Под управлением понимается совокупность операций по организации некоего процесса для достижения определённых целей.
Под термином операция в системе управления понимается получение информации, ее обработка с целью получения решения, обеспечивающего достижение поставленных целей.
Если все операции осуществимы без участия человека с использованием только функциональных элементов, тол оно (управление) называется автоматическим.
Обычно целью управления является изменение во времени по определенному закону выхода объекта управления.
Принципы управления
1) Принцип разомкнутого управления:
g(t) |
|
|
u(t) |
|
y(t) |
|
УУ |
Объект |
|||
|
|
|
|
||
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
2) Принцип компенсации возмущения:
g(t) |
|
|
u(t) |
|
|
y(t) |
|
|
УУ |
Объект |
|||||
|
|
|
|
|
|||
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) Принцип обратной связи:
g(t) |
|
|
u(t) |
|
y(t) |
|
УУ |
Объект |
|||
|
|
|
|
||
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|

4
Постановка задачи
По математическим моделям объекта управления и окружающей среды, критерию, оценивающему качество работы системы, сконструировать математическую модель управления устройством, такую чтобы эта мат. Модель могла бы быть реализована на какой-нибудь элементарной базе.
Основа математического обеспечения для решения задач конструирования систем управления
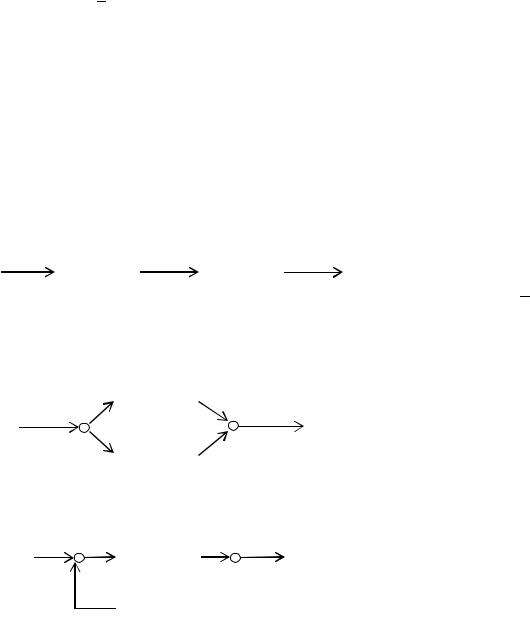
Под оператором в математике понимается правило, с помощью которого элемент одного функционального множества сопоставляется с элементами другого множества.
В теории управления под операторами понимаются правила, которые сопоставляют элементы одного функционального пространства элементам другого функционального пространства.
x(t) |
|
|
|
y(t) |
|
Оператор |
|||||
|
|
|
|
||
|
|
|
|
||
|
|
|
|
|
Виды операторов
1.Безынерционные – y(t) зависит от x(t) в тот же момент времени.
2.Инерционные - y(t) в каждый момент времени зависит от x(t) в тот же и предшествующие моменты времени.
∑ |
( )( ) |
∑ |
( )( ) – Линейное стационарное дифференциальное уравнение (линейные |
комбинации входа и выхода равны). |
|||
Если |
( ) |
и |
( ), то такое уравнение – линейное не стационарное дифференциальное |
уравнение |
|
|
|
Решение линейных стационарных дифференциальных уравнений
Прямое и обратное преобразования Лапласа
∑ ( )( ) ∑ ( )( )
– оператор преобразования Лапласа. Из линейного дифференциального уравнения получает алгебраическое уравнение.
( ) ∫ ( )
Условия, накладываемые на функцию ( ):
1. Функция должна быть тождественно равна нулю, в любой отрицательный момент времени:
( )
2. Интеграл должен сходиться:
∫ ( )

5
– обратное преобразование Лапласа.
|
|
|
( ) |
|
|
∫ |
( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f(t) |
|
|
|
|
|
F(s) |
|
|
|
|
|
f(t) |
|
|
|
|
|
F(s) |
|
|
|||||||
|
|
|
( ) |
|
( ) |
∑ ( |
)( |
) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
)( |
) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
)( |
) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
) |
|
|
|
|
|
|
|
||
( |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
) |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( ) |
|
|
|
|
|
|
|
|
||
( |
|
) |
|
|
|
|
|
|
( |
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Равенство Парсеваля
|
∫ ( ) ( ) |
|
∫ ( ) ( ) |
|
|
∫ ( ) ( ) |
|
|
|
|
|
|
|
|
|||||
Условия применения – интегралы функций ( ) |
( ) должны сходиться: |
|
|
||||||
|
|
|
∫ |
| ( )| |
∫ | ( )| |
|
|
||
Предельные соотношения: |
|
|
|
|
|
|
|
|
|
( ) |
( |
) |
|
|
( ) |
( |
) |
||
( ) |
( |
) |
|
|
( ) |
( |
) |
||
Алгоритм решения дифференциального уравнения с использованием преобразования Лапласа
∑ |
( )( ) |
|
∑ |
( )( ) |
|
|
∑ ∫ |
( )( ) |
|
∑ ∫ ( )( ) |
|
||
∑ |
( ) |
∑ |
( ) |
|
|
|
|
|
|
|
( ) |
|
|
|
|
|
|
|
|
|
|
|
( ) |
∑ |
|
|
( ) ( ) ( ) |
|
|
|
⁄ |
∑ |
||
|
|
|
|
|
||
|
|
|
|
|
|
|
Корни характеристического полинома называются полюсами. Корни числителя называются нулями.

6
( ) |
( |
) |
|
|
|
||
( |
) |
||
|
Передаточная функция системы есть отношение изображения выхода системы к изображению входа при нулевых начальных условиях.
Предположим, что
( ) |
( ) |
|
∑ |
|
|
|
|
||||
Тогда |
|
|
|
|
|
( ) |
∑ |
( ) |
|||
Если при ограниченном входе системы имеет ограниченный выход, то такая система обладает свойством устойчивости.
Система устойчива, если все полюсы лежат в левой полуплоскости. Если хотя бы один полюс лежит в правой полуплоскости, система будет неустойчивой.
Это объясняется видом функции ( ) – все полюса характеристического полинома находятся в степени экспоненты. Если хотя бы один из них имеет положительный знак (лежит в правой полуплоскости), то вся функция при будет стремиться к .
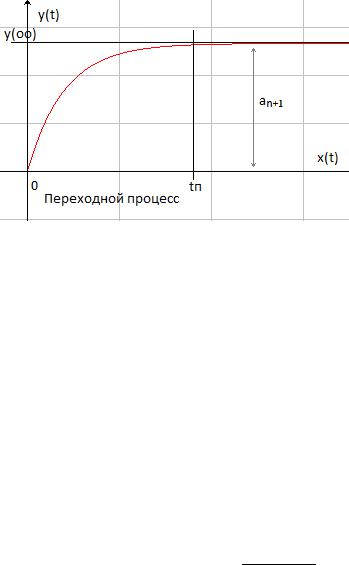
Если же все полюсы имеют отрицательный знак (лежат слева), то вся функция будет стремиться к некоторому
установившемуся значению |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример решения 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
) |
|
|
( |
) |
|
|
( |
) |
|
|
|
|
( |
) |
( |
) |
|||||||||||||
|
|
( |
) |
|
|
|
|
|
|
|
( |
|
|
|
) |
|
|
|
( ) |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
( |
|
|
|
|
|
|
|
) |
|
|
|
|
|||||||||||||||
|
|
( ) |
|
|
|
( ) |
|
|
|
|
|
( |
|
) |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
( |
|
) |
|
|
|
|
|
( |
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
( |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( ) |
|
|||
Пример решения 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
) |
|
|
( |
) |
|
|
( |
) |
|
|
|
|
( |
|
) |
|
( |
) |
|||||||||||
|
|
|
( |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
) |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
( ) |
|
|
|
( ) |
|
|
|
|
|
( |
|
) |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
( |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( ) |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
7
Переходной процесс и его оценки.
Реакция устойчивой системы на скачкообразное воздействие называется переходным процессом.
Длительность переходного процесса определяется как время от момента приложения скачкообразного воздействия до момента, в котором имеет место равенство:
| ( ) |
( )| |
| ( )| |
( ) ∑ |
( ) |
Коэффициент усиления системы – отношение реакции системы к велечине скачкообразного входа
( ( ) |
( )) в установившемся режиме, тоесть после времени . |
|
||||||||||
|
|
|
|
|
|
|
( ) |
|
|
|
|
|
Пусть ( ) |
|
|
( ) |
( ) |
|
, тогда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
( ) |
( ) |
( ) |
|
|
( ) |
|||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
( ) |
|
|
|
|
||||
|
|
|
|
|
|
|
Тоесть коэффициент усиления системы – передаточная функция системы в нулевой момент времени.
Пример
( ) ( )
Реальный воздействия могут описыватся сложными функциями времени. Обычно рассматривают поведение системы при следующих типовых воздействиях: ( ) ( ) ( ).
Чаще всего прямые оценки качества системы получают из кривой переходного процесса. Предполагается, если эти оценки удовретворительны, то системы будет функционировать удовлетворительно и при других практически любых воздействиях.
Виды переходных процессов:
1.Монотонный – первая производная не мняет знака.
2.Апереодический – знак первой производной меняется один раз.
3.Колебательный – знак первой производной меняется переодически.
8
Импульсная переходная функция
Импульсная переходная функция – реакция системы на входной сигнал вида дельта-функции.
Выходной сигнал линейной системы может быть получен как свертка его входного сигнала и импульсной характеристики системы:
( ) ∫ |
( ) |
( ) |
Для того чтобы система была физически реализуема, ее импульсная переходная функция должна удовлетворять условию: ( )=0 при . В противном случае система нереализуема, так как она нарушала бы причинно-следственную связь: отклик появляется на выходе раньше, чем на вход поступило воздействие.
|
|
|
( ) |
( ) ( |
) |
|
|
|
|
|
|
( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( ) ∫ ( ) |
∫ .∫ ( ) ( |
) / |
|
|
|
|
|
|
|
|
∫ ∫ ( ) ( |
) |
|
∫ ∫ ( ) |
( ) |
( |
) |
* |
+ |
|
|
|
|
||||||
|
∫ ∫ ( ) |
( ) |
|
∫ ( ) |
∫ ( ) |
|
|
( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( ) |
( ) |
|
|
|
|
Предел интегрирования изменяем т.к. ( ) |
при |
. |
|
|
|
|
|
||
Следовательно, передаточная функция – есть прямое преобразование Лапласа от импульсной переходной функции.
Дельта-функция и ее свойства
|
|
|
|
( ) |
{ |
|
|
|
|
|
|
|
||||
|
|
|
( |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
( ) |
( |
) |
|
|
|
|
|
|
|
∫ ( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
( ) ∫ ( ) ( |
) |
∫ ( ) ( |
) |
( ) ∫ ( |
) |
( ) |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дельта-функция имеет смысл только в нуле, в осатльных точках она равна нулю. Поэтому |
( |
) |
, только |
|||||||||||||
когда |
, т.е. |
. Тогда |
( ) можно заменить на |
|
( ) и вынесли из под интеграла как константу. |
|||||||||||
Если мы на вход системы подаем |
-функцию, то ( |
) |
|
|
( ) |
Тогда: |
|
|
|
|
||||||
|
|
|
|
( ) |
|
∑ |
|
|
|
|
|
|
|
|||
9
Связь между импульсной переходной функцией и переходным процессом
( ) ( ) ( ) ( )
Импульсная переходная функция – есть переходной процесс, от которого взята производная.
Алгебра передаточных функций
Последовательное соединение
x |
|
|
|
z |
|
|
|
y |
|
|
|
|
|
||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Параллельное соединение
|
|
|
|
|
( |
) |
|||
|
|
|
|
|
|
|
|
||
x |
|
|
|
y |
( |
) |
|||
|
|
|
|||||||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
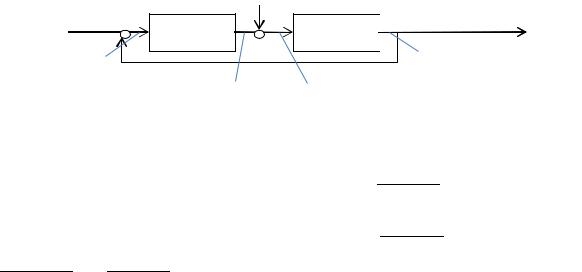
Цепь с обратной связью
x |
|
|
|
|
y |
( |
) |
|
||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
( |
) |
|
||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
( |
) |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Свойства линейных систем
Принцип гомогенности
( ) |
( ) |
( ) |
|
( ) ∫ ( ) |
∫ |
( ) |
( ) |
10
( ) |
( ) ( ) |
Принцип суперпозиции
Реакция системы на линейную комбинацию воздействий:
( ) |
( )( |
( ) |
( )) |
Реакция системы на каждое воздействие в отдельности:
|
( ) |
|
( ) |
|
( ) |
|
|
( |
) |
( |
) |
( |
) |
|
( |
) |
( |
) |
( |
) |
( ) |
( ) |
|
( ) ( ) |
( ) ( ) |
||
Система обладает принципом суперпозиций, если реакция системы на линейную комбинацию воздействий равна той же линейной комбинации реакции системы на каждое воздействие в отдельности.
Принцип наложения
|
|
|
|
||
|
( )
Реакция на одновременное воздействие:
( ( |
) |
) |
|
|
|
|
|
|
|
( ( |
) |
) |
( )
Реакция на отдельные воздействия:
( ) |
( ) |
( ) |
Сигналы действуют на систему независимо друг от друга.
Система обладает принципом наложения, если реакция системы на приложенное к ней воздействие равна сумме реакций системы на воздействия, приложенные в отдельности.
