Математические модели ограничений на реализуемость

Полосой пропусканияназывается диапазон частот гармонических колебаний, в которых выход заметно изменился.

Все физические системы характеризуются полосой пропускания. Наличие полосы пропускания связано с инерционными свойствами объектов. При большой частоте входных колебаний выход не успевает, в силу инерционности, начать движение в одном направлении, когда входное воздействие уже начинает движение в обратную сторону. Так что под действием входных колебаний высокой частоты выход практически может не меняться.

Примером нереализуемого устройства может быть дифференциатор.

С увеличением частоты амплитуда выходного сигнала возрастает до бесконечности, что невозможно. Поэтому, такая математическая модель нереализуема.

Ограничения, которым должна удовлетворять математическая модель реального объекта

Линейному дифференциальному уравнению соответствует передаточная функция:

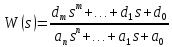
Пусть , тогда:

В модель входят дифференцирующие блоки, реализовать которые невозможно. Также невозможна реализация усилителя с коэффициентом усиления на всем частотном диапазоне.

Получим, что передаточная функция математической модели реального объекта имеет степень числителя ниже степени знаменателя.

Ограничения, которым должна удовлетворять математическая модель уу

Как правило, полоса пропускания УУ значительно шире, чем у объекта управления. Поэтому, практический интерес представляют модели УУ в полосе пропускания объекта управления.

Рассмотрим УУ с передаточной функцией . Так как УУ должен иметь такую передаточную функцию только в полосе пропускания, а не на всем частотном диапазоне – построение такого УУ допустимо.

Пусть на вход УУ подается воздействие:

Если степень числителя превышает степень знаменателя на единицу, т.е. происходит однократное дифференцирование:

То соотношение сигнал/шум уменьшится в 100 раз. Дальнейшее увеличение превышения степени числителя еще больше уменьшает это соотношение.

Из этого следует, что передаточная функция УУ и звеньев коррекции степень числителя всегда меньше либо равна степени знаменателя.

Соотношения, обеспечивающие реализуемость уу

Iслучай

Пусть

Предположим, что m>n, гдеmиn– степени числителя и знаменателя, соответственно. Запишем условия на реализуемость(а значит ии):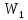

Тогда n>m:

II случай

Пусть

Тогда для реализуемости (а также) запишем соотношение:

Пусть иреализуемы. Запишем условия для реализации(а также):

Математическая модель ограничения на реализуемость в изопериметрической форме

Интегралы сходятся, если:

1. Степень числителя меньше степени знаменателя.

2. Все корни знаменателя находятся в левой полуплоскости.

Если интегралы сходятся, то справедливы неравенства:

Следовательно, справедливы следующие соотношения:

То есть из сходимости интегралов следует выполнимость ограничений.

Ограничения на реализуемость как мера качества системы управления

<Пропущено две схемы, стр. 86 учебника>

Согласно второй схеме, а также на основании равенства Парсеваля второе соотношение можно представить в виде:

Рассмотрим второе ограничение:

Правая сторона этих равенств есть не что иное, как ограничения на реализуемость. Тогда значения и интегралов характеризуют качество переходного процесса.

Корректность задачи

Корректность задачи – малым изменения в исходных данных соответствует малое изменение в решении.

Непрерывная зависимость решения от вариаций исходных данных в среднеквадратичной метрике обеспечивается, если передаточная функция удовлетворяет ограничению:

Если ограничение сопоставить с условиями на реализуемость УУ, то решаемые при ограничениях на реализуемость оптимизационные задачи всегда корректны.

Математическая модель ограничений на астатизм в системе

Система наделена астатизмом порядка , если между ее действительными желаемымвходом выполняется соотношение:

При условии, что вход изменяется по закону:

УУ конструируем таким образом, чтобы икак можно раньше совпали.

Теорема Вейерштрасса

Если – функция действительного переменного, непрерывна в конечном замкнутом промежутке, то как бы ни было мало наперед заданное положительно число, можно указать такой полином, чтобы для всехtиз рассматриваемого промежутка выполнялось соотношение:

Математическая модель

Система обладает астатизмом порядка 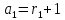, относительно задающего воздействия, если искомая функцияудовлетворяет ограничению:

Система обладает астатизмом порядка , относительно помехи, если искомая функцияудовлетворяет ограничению:

Где и– дробно-рациональные функции, не имеющие полюсов в начале координат плоскости комплексного переменного.

Математическая модель ограничения на астатизм в изопериметрической форме

Интеграл сходится, если степень числителя меньше степени знаменателя, а полюсы на мнимой оси, в том числе и в начале координат, отсутствуют.

Система обладает астатизмом порядка относительно задающего воздействия, если интеграл сходится:

Система обладает астатизмом порядка , относительно помехи, если интеграл сходится:

Ограничения на астатизм как мера качества системы управления

Если интегралы сходятся при значениях и, то они сходятся и при меньших значенияхи.

Выражения представляют собой квадратичные интегральные оценки качества разности желаемого и действительного переходных процессов при подаче на вход операторов ивоздействий видови т.д.

Интегральный квадратичный критерий оценки качества системы

Обобщенный критерий оценки качества работы:

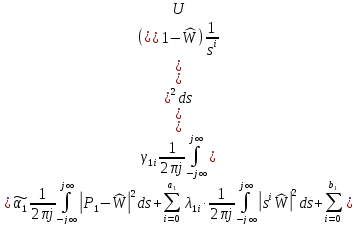
Где – весовые коэффициенты, отражающие важность соответствующих частных показателей.

Первая составляющая функционалов характеризует качество системы в установившемся режиме, относительно случайных воздействий. Все другие составляющие – качество системы в переходном режиме относительно регулярных воздействий.

Чем сложнее функционал, характеризующий качество системы, тем сложнее УУ.

Составим единый обобщенный функционал.

Примем для удобства вычислений.