
1638
.pdf
вытекает из закона больших чисел.
Ранее мы показали, что M(x) a, поэтому x - несмещённая оценка математического ожидания a. Мы показали также, что
D(x) 2 . n
Можно доказать, что если генеральная совокупность X имеет нормальное распределение, то x - эффективная оценка параметра a.
Состоятельность статистики S2 как оценки дисперсии
|
2 |
|
|
1 n |
2 |
|
|
|
2 |
|
|||
|
|
|
|
|
|
|
|||||||
S |
|
|
|
|
|
xi |
x |
|
|
||||
|
|
|
|
|
|
||||||||
|
|
|
|
n i 1 |
|
|
|
|
|
|
|||
также вытекает из закона больших чисел. Но оценка S2 – смещённая |
|||||||||||||
оценка, ведь |
|
|
|
|
|
|
|
n |
|
|
|
|
|
M(S |
2 |
) |
|
|
|
2 |
. |
||||||
|
|
|
|
|
|
||||||||
n 1
Несмещенной оценкой дисперсии 2 является исправленная
выборочная дисперсия S~2.
Чтобы оценить некоторый параметр закона распределения генеральной совокупности X, нужно выразить его через теоретические моменты (математическое ожидание, дисперсию и т.п.), а затем подставить в полученную формулу значения соответствующих выборочных статистик (выборочного среднего, выборочной дисперсии и т. д.).
Например, оценками параметров a и 2 нормального распределения служат статистики x и S~2, так как M(x)=a, D(x)= 2. Оценкой
параметров показательного |
закона является статистика (1/ |
x |
), |
т.к. |
||||
M( |
x |
)=1/ .Оценкой параметра |
закона Пуассона является статистика |
|
x |
, |
||
т.к. M(x)= .
Такой метод оценки параметров называется методом моментов. Мы фактически пользовались им в процедуре проверки гипотезы о законе распределения генеральной совокупности по критерию Пирсона.
В заключение отметим, что поправочный множитель n/(n-1), вводимый для статистики S2, при больших n практически равен 1 и его нет смысла использовать.
7.3. О ТОЧНОСТИ И НАДЁЖНОСТИ ТОЧЕЧНЫХ ОЦЕНОК
Рассмотрим здесь только случай оценки математического ожидания a генеральной совокупности значением x. Заменяя неизвестное значение a
101

|
|
|
|
|
|
|
числом x, мы совершаем ошибку. Тогда случайная величина |
|
x a |
|
|||
|
|
|
|
|
|
|
абсолютное значение ошибки. Если известен закон распределения случайной величины x, можно найти вероятность
P( x a )
Число характеризует точность оценки, вероятность - её надёжность. Если для небольших вероятность достаточно велика,
число x можно считать точной и надёжной оценкой математического ожидания a.
Когда генеральная совокупность имеет нормальное распределение,
случайная величина x распределена нормально (сумма независимых нормально распределённых случайных величин). Если закон распределения генеральной совокупности отличен от нормального, но
число n достаточно велико, случайную величину x можно считать приблизительно нормально распределённой в силу центральной предельной теоремы. Числовые характеристики x известны:
|
|
|
|
|
|
2 |
|
|
|
|
|
||||
M(x) a, |
D(x) |
, |
(x) |
||||||||||||
|
|
|
|
. |
|||||||||||
n |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
||||
Если дисперсия генеральной совокупности неизвестна, заменим её на
значение исправленной выборочной дисперсии S~2. Применяя известную формулу для нормального закона, получим
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
n |
|
|
|
|
|
||||||||||||||
P ( |
|
x a |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
) 2 |
|
|
|
|
2 |
|
|
|
2 |
|
~ |
. |
|||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
S |
|
||||
Пример. Из генеральной совокупности извлечена выборка объёма n=47. Найденное по выборке значение S~ =2,35. Какова вероятность того, что точность оценки математического ожидания a генеральной совокупности не больше 0,3?
Решение. Нужно найти вероятность события
P x a 0,3 .
Имеем |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
0,3 |
|
|
|
|
|
|
|
|
|
|
n |
47 |
2 0,875 2 0,31 0,62. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
P |
x a |
|
0,3 2 |
|
~ |
|
|
2 |
2,35 |
|
|
|||||
|
|
|
||||||||||||||
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|||
Найденная вероятность достаточно мала. Для того чтобы получить большую надёжность (при той же точности) или большую точность (при той же надёжности), нужно увеличить число n.
Пример. Каков должен быть минимальный объём выборки n для того, чтобы с надёжностью 0,98 точность оценки математического ожидания a с
102

помощью выборочного среднего x была 0,2, если среднее квадратичное отклонение генеральной совокупности равно 1,5?
Решение. Число n определяется из условия
P x a 0,2 0,98,
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,2 |
n |
|
0,2 |
n |
||||||
0,98 2 |
|
|
|
2 |
|
|
|
||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
. |
|||
|
|
|
|
|
1,5 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
0,2 |
|
|
|
2 |
|
|
|
2,34 15 |
|||
n |
n |
|
||||||||||
|
|
|
|
|
0,49 |
|
|
2,34 n |
|
|
308. |
|
|
|
|
|
|
|
|||||||
|
1,5 |
|
|
|
15 |
|
|
2 |
|
|||
|
|
|
|
|
|
|||||||
Пример. Как изменится точность математического ожидания a из предыдущего примера, если объём выборки увеличить до 500, а надёжность оставить равной 0,98?
Решение. Из условия
P x a 0,98
получаем, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
500 |
|
500 |
||||||||
0,98 2 |
|
|
|
|
|
|
|
|
|
2,34 0,157. |
|
|
|
|
|
|
|
||||
|
|
1,5 |
|
|
|
1,5 |
|
|
||
|
|
|
|
|
|
|
||||
Пример. Оценка вероятности p “успеха”.
Пусть проведено n независимых испытаний, в каждом из которых вероятность события A (“успеха”) равна p (следовательно, вероятность непоявления события A равна q=1-p). Если в n независимых испытаниях событие A появилось k раз, то насколько точно число k/n оценивает вероятность p?
Решение. В этом случае генеральная совокупность X имеет следующий закон распределения:
Xi |
0 |
1 |
pi |
q |
p |
Случайная величина X равна единице, если событие A произошло, и равна нулю в противном случае.
M(X)=p, D(X)=pq, X 
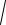 pq.
pq.
Если число n достаточно велико, то случайная величина x= k/n - выборочное среднее - имеет приближённое нормальное распределение с параметрами:
M |
|
p, |
D |
|
|
pq |
, |
|
|
|
pq |
. |
|
x |
x |
x |
|||||||||||
|
|
||||||||||||
|
|
|
|
|
|
n |
|
|
|
n |
|||
103

Тогда точность и надёжность оценки числа p числом k/n определяют из равенства
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
n |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
P |
x p |
|
2 |
|
|
|
2 |
|
|
|
|
, |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x(1 x) |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
так как |
|
|
|
|
|
|
|
|
|
|
|
|
pq |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
0 |
2 n k 12 k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
k |
|
k |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 x , |
|||||||||||||||||||||||||||||
S2 |
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||||||||||||||||||||||
n |
|
|
|
n |
n |
2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
n |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
(1 |
|
|
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
x |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Пример. Из большой партии некоторых изделий отобрано наугад для контроля 500 штук, причём 20 штук оказались бракованными. Найти вероятность того, что, приняв вероятность p изделию быть бракованным, равной 0,04, мы совершаем ошибку, не превосходящую 0,01. Сколько нужно отобрать изделий, чтобы с вероятностью 0,95 была совершена ошибка, не превосходящая 0,01?
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
0,04 0,96 0,0384; |
||||||||||||||||
1. Здесь |
|
|
|
|
20 |
|
0,04; |
n 500; |
S2 |
|
|
|
|
|
|||||||||||||||||||||
x |
|
x |
x |
||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||
|
500 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
S |
|
|
0,2; |
|
0,01. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
0,0384 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Положим |
|
|
|
S |
|
0,009. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
P |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,01 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
500 |
2 1,14 0,746. |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
x p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
0,01 2 |
|
0,2 |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2. |
Здесь |
x |
0,04; S 0,2; 0,01; 0,95.Требуется найти объём |
||||||||||||||||||||||||||||||||
выборки n. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,01 |
|
n |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,475 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
0,2 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
По таблице функции Лапласа, зная её значение, равное числу 0,475, определяем аргумент
0,01 |
|
|
|
|
1,96 0,2 |
|
2 |
|
n |
|
|
||||||
t |
|
|
1,96, |
отсюда n |
|
|
1537. |
|
|
|
0,01 |
||||||
0,2 |
|
|
|
|
|
|
||
7.3.1. Ещё об определении нужного объёма выборки
Пользуясь формулой
104
|
|
|
|
|
|
n |
|
|
|
n |
|
|
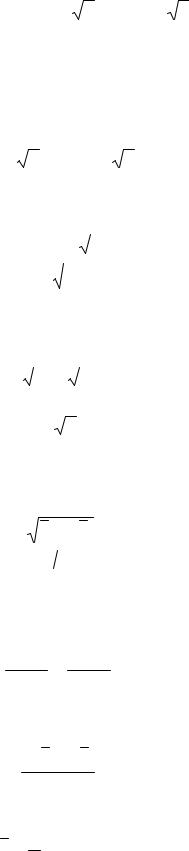
P |
x a |
2 |
|
2 |
, |
|||||||
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
можно поставить три несложные задачи. Примеры решения этих задач уже были подробно разобраны выше. Здесь мы просто подведём итоги. Задача 1. Зная объём выборки n и точность оценки математического
ожидания a, найти надёжность этой оценки:
|
|
|
n |
|
|
|
|
n |
|
|
2 |
|
|
2 |
|
|
|||||
|
|
|
|
|||||||
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
В случае выборки из биномиально распределённой совокупности
|
|
|
|
|
|
|
|
|
|
||
|
n |
||||||||||
|
|
|
|
|
|
|
|||||
2 |
|
|
|
|
|
|
|
|
. |
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|||||||
|
|
x1 x |
|||||||||
Задача 2. Зная объём выборки n и надёжность , оценить точность
оценки математического ожидания a: |
|
|
|
|
|
|
||
|
t |
|
|
tS |
, |
|||
|
|
|
|
|
|
|||
|
|
n |
|
|
|
n |
||
где число t определяется из таблицы функции Лапласа из условия
|
|
n |
|
|
||
t |
|
|
|
|
|
. |
|
|
|
||||
|
|
|
|
2 |
|
|
|
|
|
|
|||
В случае выборки из биномиально распределённой генеральной совокупности
tx1 x
 .
.
 n
n
Задача 3. Зная точность и надёжность оценки математического ожидания a, определить минимальный объём n выборки, обеспечивающий заданные точность и надёжность:
n t2 2 t2S2 .
2 2
В случае выборки из биномиально распределённой генеральной совокупности
nt2 x1 x .
2
Все эти формулы были выведены в предположении, что
1 n
x Xi, n i 1
105

где X1, X2, ..., Xn - независимые и одинаково распределённые (как генеральная совокупность X) случайные величины. Такое предположение не всегда можно принять. На практике генеральная совокупность X - это N объектов, из которых отбирают для исследования n объектов. Если выборка бесповторная (один раз отобранный объект не возвращается назад), то дисперсия выборочного среднего x в общем случае зависит от чисел N и n.
Пусть генеральная совокупность X состоит из N чисел x1, x2, ..., xN. Если вероятность выбора каждого числа (при извлечении одного числа) равна 1/N, то математическое ожидание a и дисперсия 2 случайной величины x - выбранного числа - равны соответственно:
|
1 |
N |
|
a |
xi; |
||
|
|||
|
N i 1 |
||
2 1 |
N |
xi2 a2. |
N i 1
Пусть теперь x - это среднее арифметическое n наудачу отобранных чисел, причём отбор бесповоротный. Нетрудно показать, что в этом случае
|
|
|
|
|
|
2 |
|
N n |
|
2 |
|
n |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|||||||||
M x a; |
D x |
|
|
1 |
. |
|||||||||||||||||
|
|
|
|
|
1 |
|
; |
x |
|
|
|
|
|
|||||||||
n |
N 1 |
n |
|
|
n |
|
N |
|||||||||||||||
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|||||||
На практике величину 
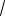 1 n/ N заменяют на 1, если n/N<0,05, и рассчитывают в противном случае. Для отыскания необходимого объёма выборки, обеспечивающего заданную точность и надёжность, имеем:
1 n/ N заменяют на 1, если n/N<0,05, и рассчитывают в противном случае. Для отыскания необходимого объёма выборки, обеспечивающего заданную точность и надёжность, имеем:
|
|
n |
|
|
|
t, |
n |
|
2t2N |
|
|
|
S2t2N |
|
. |
||
|
|
|
|
|
|
|
|
|
2N 2t |
2 |
|
2N S2t |
2 |
||||
|
1 |
|
n |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|||
Если среди чисел x1, x2, ..., xN встречаются только нули и единицы, то
|
|
|
1 |
|
|
t2N |
||||
n |
|
x |
x |
|||||||
|
|
|
|
|
. |
|||||
2N |
|
|
1 |
|
t2 |
|||||
x |
x |
|||||||||
Напомним, что пользоваться указанными формулами можно, только если закон распределения выборочного среднего x можно хотя бы приближённо считать нормальным. Так почти всегда получается, когда n>30.
Пример. Фермер хочет оценить среднюю массу своих 5000 индеек с точностью до 0,5 фунта, чтобы как можно точнее определить доход от продажи этих индеек. Отобрав случайным образом 20 индеек, он нашёл, что их средняя масса составляет 9,25 фунта, а S~=4,39 фунта. Теперь он в состоянии определить минимальный объём выборки n, позволяющий оценить среднюю массу индейки с точностью =0,5 и надёжностью
=0,95:
106

n |
|
S2t2N |
|
|
4,392 1,962 |
5000 |
||
|
|
|
|
|
|
|
280(штук). |
|
|
2N S2t |
|
0,52 5000 4,392 |
|
||||
|
|
2 |
|
1,962 |
||||
Предварительная малая выборка потребовалась, чтобы оценить , иначе дальнейшие вычисления невозможны.
7.4. ПОНЯТИЕ ОБ ИНТЕРВАЛЬНЫХ ОЦЕНКАХ ПАРАМЕТРОВ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ
Ещё один способ оценить известное значение параметра - указать интервал 1, 2 на числовой оси, про который известно, что он содержит это неизвестное значение с достаточно большой вероятностью
,P 1 a 2 .
Вероятность называется доверительной вероятностью, а интервал1, 2 - доверительным интервалом. Для построения доверительных интервалов используют подходящим образом подобранные выборочные статистики.
7.4.1. Построение доверительного интервала для неизвестного математического ожидания a
нормально распределённой генеральной совокупности, когда дисперсия σ2 генеральной совокупности известна
Рассмотрим случайную величину x - выборочное среднее:
1 n
x xi. n i 1
Taк как генеральная совокупность X распределена по нормальному закону, x тоже имеет нормальное распределение, M(x) a, D(x)= 2/n.
График функции плотности вероятности случайной величины x симметричен относительно оси x=a.
Рассмотрим интервал x a , или a x a . Ширину 2 этого интервала определим из условия
P x a ,
где - заданная доверительная вероятность.
Как мы уже знаем, t , где число t находится по таблице функции
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|||||||
Лапласа из условия t |
|
|
|
|
|
|
|
. |
|
|
|
|
|
||||
|
|
|
|
|
2 |
|
||
|
|
|
|
|
||||
107
Доверительный интервал (x-t /
 n , x+t /
n , x+t /
 n ) содержит число a с вероятностью .
n ) содержит число a с вероятностью .
Приведём значения t для наиболее часто встречающихся значений вероятности .
|
0,9 |
0,95 |
0,99 |
0,9973 |
0,999 |
t |
1,64 |
1,96 |
2,58 |
3,00 |
3,37 |
Пример. У ста случайно отобранных двадцатилетних юношей измерили рост. Оказалось, что средний рост x=1,73 м, а исправленная
выборочная дисперсия S~2=0,00245 м2. Построить доверительный интервал среднего всей совокупности, если =0,99.
Решение. Подразумевается, что случайная величина X - рост юноши - имеет нормальное распределение с неизвестными нам параметрами a и Так как объём выборки n велик, то вместо неизвестного значения можно взять значение S~ 
 0,00245 0,0495. Если =0,99 => t=2,58. Отсюда:
0,00245 0,0495. Если =0,99 => t=2,58. Отсюда:
|
tS~ |
|
|
2,58 0,0495 |
0,013; 1,717<a<1,743. |
|
|
|
|
||||
|
|
n |
10 |
|
||
Подчеркнём, что условие P 1 a 2 следует интерпретировать следующим образом. Случайный интервал ( 1, 2) со случайными границами 1, 2 с вероятностью содержит неслучайное число a.
7.4.2. Построение доверительного интервала для неизвестной вероятности p “успеха”
Пусть в серии из n независимых испытаний “успех” произошел k раз. Требуется построить доверительный интервал, содержащий значения вероятности p появления “успеха” в каждом испытании с данной вероятностью .
В этом случае генеральная совокупность X распределена по закону
xi |
0 |
1 |
pi |
q=1-p |
p |
M(X)=p, D(X)=pq.
Выборка, соответствующая k появлениям “успеха” в n независимых испытаниях, имеет вид
xi |
0 |
1 |
ni |
n-k |
k |
Выборочное среднее x k/n можно считать приближённо нормально распределённым только в случае большего числа испытаний. Но если это условие выполнено, можно воспользоваться таблицей функции Лапласа,
108

подставив в формулу для вместо неизвестного среднего квадратического отклонения генеральной совокупности исправленное выборочное среднее квадратическое отклонение S~:
S~ |
S~2 |
|
n |
S2 |
n |
|
|
|
|
2 . |
|
x |
x |
||||||||||
|
|
||||||||||
|
|
|
n 1 |
n 1 |
|||||||
Причём если n велико, то подправлять S нет смысла. Окончательно определяется по формуле
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tS |
|
|
t |
|
1 |
|
|
, |
||||
|
|
x |
x |
||||||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
n |
|
|
n |
||||||||
где число t берётся из таблицы функции Лапласа из условия Ф t /2. Пример. В 100 бросаниях монеты герб выпал 64 раза. Построить
доверительные интервалы для вероятности p выпадения герба в одном бросании с доверительными вероятностями 1 0,9; 2 0,95; 3 0,99.
Можно ли считать монету правильной?
Решение. Здесь n=100; k=64; t1=1,64; t2=1,96; t3=2,58; выборочное среднее x 0,64; выборочная дисперсия S2 x1 x 0,64 0,36 0,2304;
выборочное среднее квадратическое отклонение S 
 S2 0,48. Число опытов n велико, поправкой для дисперсии можно пренебречь.
S2 0,48. Число опытов n велико, поправкой для дисперсии можно пренебречь.
|
|
t1 |
S |
|
|
1,64 0,48 |
|
0,079, |
|
2 |
|
t2 |
S |
|
1,96 0,48 |
0,094, |
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
1 |
|
|
n |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
n |
10 |
|
||||
|
|
|
|
t3S |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
2,58 0,48 |
|
|
|
||||||||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
0,124. |
|||||
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
||||
Границы доверительных интервалов для вероятности p таковы: 0,561<p<0,719, если =0,9; 0,546<p<0,734, если =0,95;
0,516<p<0,764, если =0,95.
Ни один из этих интервалов не содержит числа 0,5. Монету следует признать неправильной, вероятность p выпадения герба больше 0,5.
7.4.3. Построение доверительного интервала для неизвестного математического ожидания нормально распределённой генеральной совокупности, когда дисперсия σ2 генеральной совокупности неизвестна
Как уже было сказано выше, когда объём выборки n>30, при построении доверительного интервала для a можно пользоваться нормальным распределением, подставляя в формулу для ширины
109

интервала вместо неизвестного значения число S~, определяемое по выборке. Рассмотрим случай малых n.
В этой ситуации пользуются случайной величиной T, определяемой формулой
|
x a |
|
|
|
x a |
|
|
|
|
T |
|
n 1 |
|
n. |
|||||
|
|
~ |
|
||||||
S |
|||||||||
|
|
|
|
S |
|
|
|
||
Подчеркнём, что x и S - это случайные величины, а n и a - числа. Случайная величина T распределена по закону Стьюдента (Стьюдент -
псевдоним английского статистика В. Госсета (1876-1937), одного из создателей теории проверки статистических гипотез).
График функции плотности вероятности случайной величины, распределённой по закону Стьюдента, симметричен относительно оси ординат. Функция плотности f(t, r) зависит от одного параметра r, который называется числом степеней свободы.
Случайная величина
|
x a |
|
|
|
x a |
|
|
|
T |
|
n 1 |
|
n |
||||
|
|
~ |
|
|||||
S |
||||||||
|
|
|
|
S |
|
|
||
имеет число степеней свободы r=n-1.
Для распределения Стьюдента составлены специальные таблицы, по которым, зная число степеней свободы r и вероятность события T t ,
можно найти число t . Таблица распределения Стьюдента приведена в
прил. 2.
Заключим случайную величину T в интервал, симметричный относительно нуля, и обозначим его границы через -t и t .
P T t .
Тогда вероятности событий T t и {T<tβ} равны:
P(T>tβ)=P T t 1 . 2
Зная число степеней свободы r=n-1 и вероятность (1- )/2, можно по таблице найти число t . Неравенство T t означает, что
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
t . |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Раскрывая знак модуля, получаем, что |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
t S~ |
|
|
|
t S~ |
|
|
|
|
|
t S |
|
|
|
t S |
||||||||||||||
|
x |
a x |
|
x |
a x |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
, или |
|
|
|
|
|
|
|
. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
n |
|
|
|
|
n |
|
|
|
|
|
|
n 1 |
|
|
|
|
n 1 |
||||||||||
110
