1547

колебаний достигает наибольшего значения, называется резонансом.

Рис. 3. Резонансная кривая

Можно показать, что частота, при которой наступает резонанс, связана с частотой собственных колебаний системы и коэффициентом затухания соотношением

4.Сложение перпендикулярных колебаний. Фигуры Лиссажу

Рассмотрим систему, которая может совершать колебания в двух взаимно перпендикулярных направлениях. Траектории, которые может иметь тело при этом, получили название фигур Лиссажу. Их вид зависит от соотношения частот и разности фаз колебаний. При этом выполняется несколько важных закономерностей, которые широко используются для настройки и анализа колебательных систем:

а) отношение количества пересечений оси Х к количеству пересечений оси Y равно отношению частот колебаний;

б) вид фигуры Лиссажу зависит от разности фаз колебаний.

5. Метод решения задач механики с использованием вычислительной техники

Любую механическую задачу можно свести к решению так называемых дифференциальных уравнений (или систем дифференциальных уравнений), частным случаем которых являются

10

уравнения Ньютона, которые описывают движение под действием различных сил, зависящих в общем случае от положения точки в пространстве, ее скорости и момента времени:

a F(x, ,t)/m.

Решение данных уравнений аналитическими способами в общем случае является очень сложной, часто просто невыполнимой задачей. Для получения решений в настоящее время разработано большое количество численных способов, основанных на использовании вычислительной техники. Простейшим из них, который использован в данной лабораторной работе, является метод, разработанный еще самим Ньютоном. Он заключается в том, что соответствующие производные заменяются так называемыми конечно-разностными соотношениями, т.е. например:

x(t1) x(t2 ) и a (t1) (t2 ).

Тогда в качестве решения задачи можно предложить следующий алгоритм:

1. Во-первых, вычисляется значение ускорения в данный момент времени с использованием известной силы:

aF(x, ,t)/m.

2.Во-вторых, вычисляется значение скорости с использованием конечно-разностных соотношений:

x(t2 ) x(t1 ) a (t2 t1 ).

3. В-третьих, вычисляется новая координата точки с использованием конечно-разностных соотношений:

x(t1 ) x(t1 ) υ(t2 t1 ).

4. В-четвертых, вычисляется новое значение времени: t3 t2 t.

5. И наконец, возвращаемся к пункту 1 и получаем новое значение координаты и т.д.

В качестве дифференциального уравнения колебательного движения используется уравнение вынужденных колебаний.

Задание к лабораторной работе

Для работы с программой в главном меню (рис. 4) выберите необходимый тип колебательного движения.

11

Рис.4. Главное меню

Рис.5. Рабочее окно программы

12

Упражнение 1. Гармонические колебания

1.Введите значения коэффициента упругости пружины и массы подвешенного тела. Перечертите полученный график колебаний с монитора или распечатайте его с помощью принтера (рис. 5).

2.Выберите произвольно некоторое число колебаний и определите время, за которое они произошли. Рассчитайте период колебаний по формуле (2). Сравните его с теоретическим периодом колебаний пружинного маятника, подсчитанным по формуле (1).

3.Проведите измерения периода несколько раз, занесите результаты измерений в табл. 1.

4. Сделайте вывод, от чего зависит период и частота гармонических колебаний?

Упражнение 2. Затухающие колебания

1.Введите значения коэффициента упругости пружины, массы подвешенного тела и коэффициента упругости среды. Перечертите полученный график колебаний с монитора или распечатайте его с помощью принтера.

2.Измерьте амплитуду колебаний при двух моментах времени А1

иА2. Определите коэффициент затухания ар по формуле (6). Сравните его с коэффициентом затухания ат, рассчитанным по формуле (3).

3.Определите период колебаний Тр по методике, изложенной в первом упражнении, сравните с периодом колебаний Тm, подсчитанным по формуле (4).

13

4.Определите расчетный логарифмический декремент λ затухания по формуле (5).

5.Проведите измерения несколько раз, занесите результаты измерений в табл. 2.

Таблица 2

Результаты измерений

6. Сделайте вывод о совпадении (или несовпадении) расчетных и теоретических значений.

Упражнение 3. Вынужденные колебания

1.Введите параметры установки, а также амплитуду и частоту вынуждающей силы. Перечертите полученный график колебаний с монитора или распечатайте его с помощью принтера.

2.Проведите исследования зависимости амплитуды вынужденных колебаний от частоты вынуждающей силы.

Данные занесите в табл. 3. Используя данные таблицы, постройте резонансную кривую.

Таблица 3

Результаты измерений

ν, Гц

А, м

3.Определите по графику резонансную частоту, подсчитайте её значение по формуле (8), сравните полученные расчетные и теоретические значения ν.

4.Измерьте резонансную амплитуду вынужденных колебаний Ар. Сравните ее с амплитудой Ат, подсчитанной по формуле (7).

14

5. Сделайте вывод, от чего и как зависит амплитуда установившихся вынужденных колебаний?

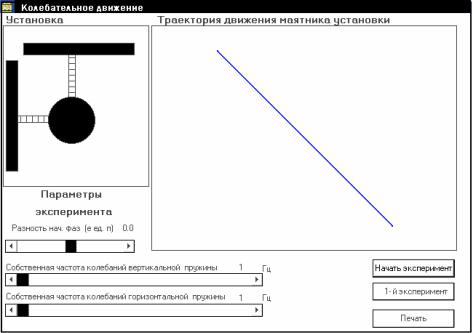
Упражнение 4. Двухмерные колебания

1. Выберите пункт меню «Взаимно перпендикулярные колебания».

Рис.6. Рабочее окно программы

Введите параметры установки, рекомендуемые преподавателем. Зарисуйте полученные графики траекторий в табл. 4 (рис. 6).

2. В выводе отметьте, от чего и как зависит вид фигур Лиссажу, какие параметры колебаний могут быть получены при анализе этих кривых?

15

ЛАБОРАТОРНАЯ РАБОТА № 2 (7К)

Основы термодинамики

Цели работы: исследование термодинамических процессов, производимых в идеальном газе. Проверка первого начала термодинамики, расчет теплоемкости газа.

Основы теории

Раздел физики, изучающий свойства тел без использования представлений о характере движения и взаимодействия частиц, из которых они состоят, называется термодинамикой.

Термодинамика рассматривает свойства тел и явления, происходящие в них, опираясь на общие законы (начала) термодинамики. Законы термодинамики и молекулярно-кинетическая теория дополняют друг друга.

Первоначально термодинамика возникла как наука об использовании теплоты для получения работы (теоретическая теплотехника). Одновременно были открыты законы термодинамики, обладающие большой общностью. Эти законы относятся к преобразованиям энергии, ее изменениям в различных процессах и к ряду связанных с ней величин. Поэтому основное содержание современной термодинамики можно определить как учение о наиболее общих свойствах макроскопических систем и о закономерностях тепловых, а также ряда других физических явлений.

Внутренняя энергия. Одним из важнейших параметров термодинамической системы является ее внутренняя энергия. Внутренней энергией системы называют ту часть ее полной энергии, которая определяется собственными параметрами этой системы. Внутренняя энергия тела складывается из кинетической энергии хаотического теплового движения и потенциальной энергии их взаимодействия. Кинетическая и потенциальная энергии тела как целого во внутреннюю энергию не входят.

Внутренняя энергия идеального газа. Внутренняя энергия идеального газа представляет собой сумму кинетических энергий теплового движения его частиц. В статистической физике выводится закон Больцмана о равномерном распределении энергии по степеням свободы. На каждую поступательную и вращательную степень

16

свободы приходится энергия, равная kT , на каждую колебательную

2

– кТ.

При этом без учета колебательных степеней свободы, которые "включаются" при высоких температурах, для одноатомного газа i =3, для двухатомного i = 5, для многоатомного i = 6.

Средняя кинетическая энергия молекул газа, таким образом,

равна i kT . Поэтому внутренняя энергия идеального газа, состоящего

Рис.1. Работа в термодинамике

Внутренняя энергия идеального газа зависит только от одного параметра – его абсолютной температуры: U = f(T).

Работа в термодинамике. По определению работы δA=Fdl, но

F=pS , a Sdl = dV => δA = pdS.

Тогда полная работа

V2

A pdV .

V1

17

Как видно из полученного выражения, работа положительна при увеличении объема и отрицательна при его уменьшении. Согласно свойствам интеграла, работа также определяется площадью под кривой процесса в координатах рV (рис. 1).

Первый закон термодинамики. Внутренняя энергия изолированной термодинамической системы может изменяться двумя способами: при совершении работы и при теплообмене (теплопередаче).

В термодинамической системе количество переданной теплоты δQ идет на изменение внутренней энергии dU и совершение системой работы δA внешних сил:

δQ = dU+δA.

Первое начало термодинамики является законом сохранения энергии для термодинамических процессов.

Применение первого закона термодинамики к различным процессам

Изотермический процесс. В идеальном газе внутренняя энергия определяется абсолютной температурой. При изотермическом расширении или сжатии газа его температура не меняется. В изотермическом процессе изменение внутренней энергии равно нулю:U =0. На основании первого закона термодинамики при изотермическом расширении газа переданное количество теплоты Q равно работе А, совершенной газом: Q = A.

Работа же в данном процессе

Изохорный процесс. При изохорном процессе работа газа равна нулю, поэтому изменение внутренней энергии ΔU идеального газа равно полученному количеству теплоты Q.

Итак, при изохорном процессе Q = ∆U = i m R T .

2 M

Изобарный процесс. Изобарное расширение газа происходит при передаче ему количества теплоты Q. В результате нагревания газа происходит увеличение его внутренней энергии и совершение работы расширения: Q U A U p V .

Адиабатный процесс. Адиабатным называется процесс

18