Линейная алгебра

Загрузка пакета >with(linalg):

Задание вектора

1) координатами >a: =vector([2,3,4]);a: = [2,3,4]

2) некоторыми первыми координатами с указанием размерности вектора

>b: = vector(4,[2,3]); b: = [2, 3, b3, b4]

Незаданные координаты b3 ,b4 можно в дальнейшем вычислять или задавать

>b[3]:=2^3+4:b[4]:=2^5–1:

>print(b); вывести на экран векторb[2, 3, 12, 31] .

3) Задание нулевого вектора >a:=vector(5,0);a:=[0,0,0,0,0].

4) Задание координат как функций от номера >a:=vector(3,x–>f(x));a:=[f(1),f(2),f(3)].

(аргумент функции можно обозначать любой буквой).

Функцию можно задавать заранее:

>f:=n–>n^3;

>b:=vector(4, f); b:=[1, 8, 27, 64]

или

>h:=n–>diff(x^5,x$n); (вMAPLE 11 можно писатьh:=n–> (x⁵)⁽ⁿ⁾ )

>u:=vector(3, h); u:=[5x⁴, 20x³, 60x²] .

Примечание. n -ю координату вектора «а» можно вывести на экран командой >a[n];

Полностью любой вектор «а» выводится на экран командой >print(a);

Задание матрицы.

1) строками >A:=matrix([[1,2,3],[4,5,6]]); .

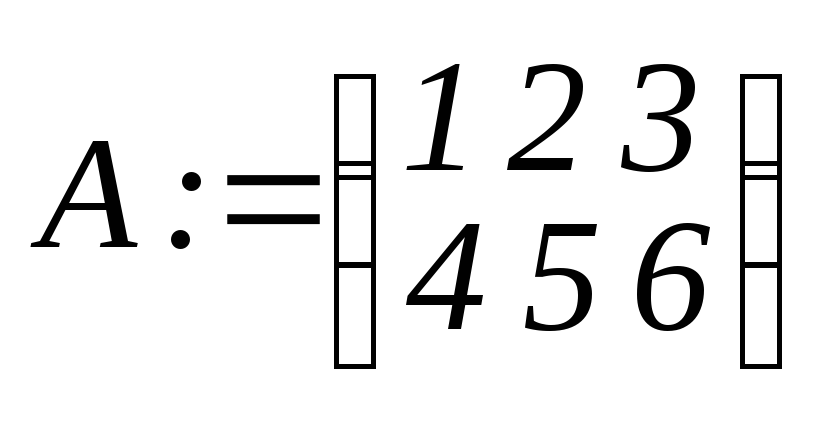2) задать число строк (= 3) и число столбцов (= 2), а затем в квадратных скобках записывать через запятую элементы матрицы как строчки в книге

>A:=matrix(3,2,[1,2,3,4,5,6]); .

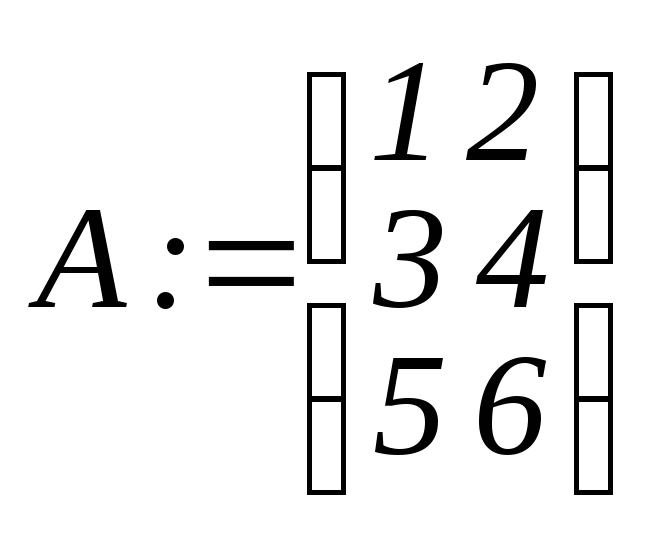3) нулевая матрица, содержащая m строк и n столбцов, задается командой >A:=matrix(m,n,0);

4) единичная матрица n n задается командой >Е:=array(1..n,1..n,identity);

5) матрица может быть задана функцией от номера строки mи номера столбцаn

>F:=(m,n)–> 10*m+n:

>A:=matrix(2,3,F); .

Примечание.Для произвольной матрицы А можно вывести на экран командами

>A[m,n]; элементm-й строки иn-го столбца,

>row(A,n); полностьюn-ю строку,

>col(A,n); пполностьюn-й столбец .

Полностью матрица Aвыводится на экран командой >print(A);

Основные задачи линейной алгебры

ВЕКТОРЫ

1) Линейные операции над векторами, задаваемыми без слова vector, можно производить без подгрузки пакетаlinalg.

>a:=[1,2,3]; >b:=[1,1,1];

>c:=2*a–3*b; Ответ: c:=[–1,1,3]

Для линейных операций над векторами a:=vector([1,2,3]); >b:=vector([1,1,1]); следует подгрузить пакетlinalgи выполнять линейные операции с использованием команды оцениванияevalm

>c:=2*a–3*b; Ответ:c:=2a–3b– отложенная команда

>evalm(c); Ответ: [–1,1,3] – вычисление линейной комбинации.

2) Скалярное произведение двух векторов а иb

>dotprod(a,b);

Здесь векторы могут задаваться в форме >b:=[b1,b2,b3] , без словаvector.

3) Нахождение угла между векторами а иb

>angle(a,b);

Здесь векторы могут задаваться в форме >b:=[b1,b2,b3] , без словаvector.

4) Векторное произведение двух векторов а иb

>crossprod(a,b);

Здесь векторы могут задаваться в форме >b:=[b1,b2,b3] , без словаvector.

5) Нахождение базиса для произвольной системы векторов {a,b,c,d}

>basis({a,b,c,d});

6) Ортогонализация системы {a,b,c,d} линейно независимых векторов

>GramSchmidt({a,b,c,d}); [e1,e2,e3,e4] – система ортогональных векторов.

7) Норма вектора и его нормализация (координаты вектора делятся на его длину)

>a:=[3, 4];a:=[3, 4] задание вектора (можно без словаvector)

>norm(a,2); 5 – норма (длина) вектора

>normalize(a); нормализация вектора, ответ: [3/5 , 4/5] .

МАТРИЦЫ

1) Линейная комбинация заданных матриц А и В

>evalm(2*A–3*B); Примечание: А+5 вычисляется как А+5*Е

Умножение матриц подходящих размеров

>evalm(A&*B);

Деление на невырожденную матрицу В (умножение справа на В^–1)

>evalm(A/B); Примечание: команда >evalm(1/B); вычисляет В^–1.

Рекомендация. Удобно сначала провести все выкладки с матрицами без команды оценивания, а затем выполнить команду оценивания >evalm(…); Например:

>((2*A+3)&*B)/C; (при делении ставить скобки!)

>evalm(%);

2) Вычисление определителя квадратной матрицы А >det(A);

3) Транспонирование матрицы А >transpose(A);

4) Для данной квадратной матрицы А вычисляется присоединенная матрица В (т.е. транспо­нированная матрица из алгебраических дополнений)

>B:=adj(A);

5) Вычисление обратной матрицы для квадратной матрицы А , если det(A)0

>inverse(A);

6) Элементарное преобразование матрицы A: поменять местамиm-йи n-йстолбцы

>swapcol(A,m,n);

Аналогичная операция со строками осуществляется командой >swaprow(A,m,n);

7) Элементарное преобразование матрицы A: Умножениеn-го столбца на числох

>mulcol(A,n,x);

Аналогичная операция со строкой производится командой >mulrow(A,n,x);

8) Элементарное преобразование матрицы A: столбец с номеромm умножается на числох и прибавляется к столбцу с номеромn

>addcol(A, m, n, x);

Аналогичную операцию со строками производит команда >addrow(A,m,n,x);

9) В матрице А выбирается ненулевой элемент A[m,n] и во всех строках над ним и под ним делаются нули при помощи элементарных преобразований

>pivot(A,m,n);

10) Вычеркивание из матрицы А столбцов с номерами от m доn

>delcols(A,m..n);

Если m=n, то удаляется только один столбец. Аналогичная команда для строк имеет вид

>delrows(A,m..n);

11) Приведение матрицы А к ступенчатому виду

>A:=matrix(3, 3, [9,8,7,6,5,4,3,2,1]); 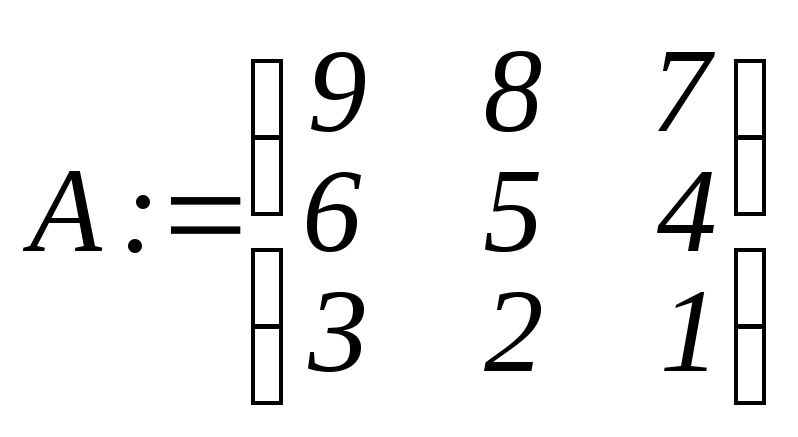задание матрицы.

>gausselim(A); 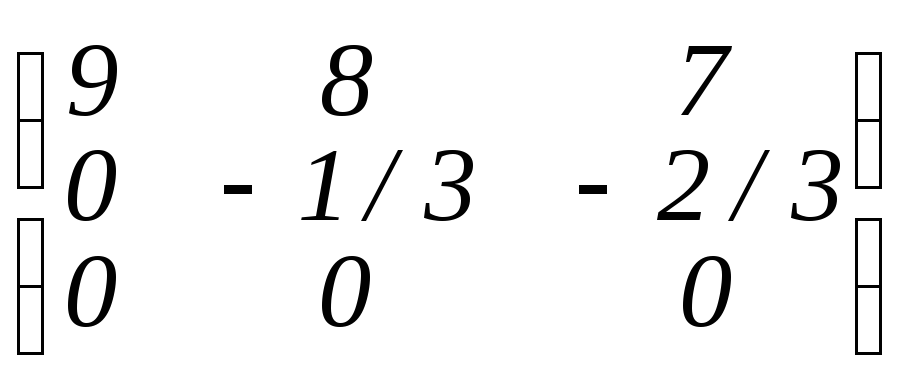(в ответе возможны дроби).

>ffgausselim(A); 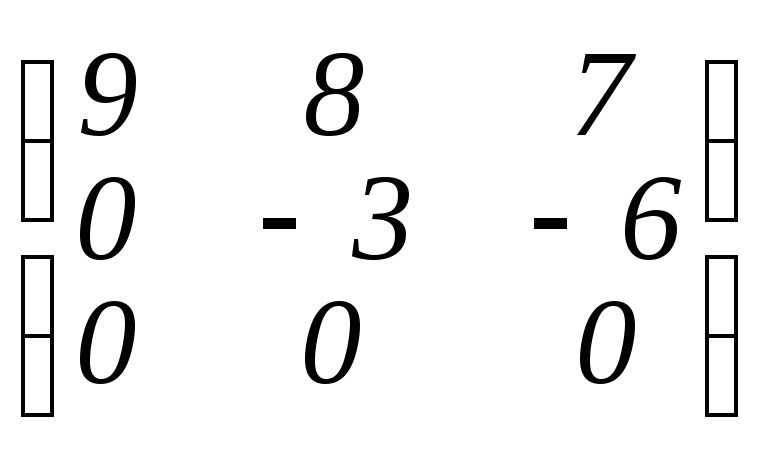(в ответе дроби отсутствуют).

>gaussjord(A); приведение матрицы к главному ступенчатому виду.

12) Ранг матрицы А >rank(A);

13) Нахождение характеристического многочлена для квадратной матрицы А

>P:=charpoly(A,lambda); (вместоможно употребить любую другую букву). Команда вычис­ляет характеристический многочлен матрицы А.

Собственные числа матрицы А (корни этого характеристического многочлена) находятся затем командой

>solve(P,lambda);

14) Вычисление собственных значений матрицы А >eigenvals(A);

Ответ записывается в точном виде, если элементы матрицы заданы точно. Если же элементы матрицы заданы в десятичном виде, то собственные значения будут вычисляться приближенно.

15) Вычисление собственных значений (с указанием кратности) и соответствующих собствен­ных векторов

>A:=matrix(2, 2, [5,4,3,9]): задание матрицы А

>eigenvects(A); [3, 1, {[–2, 1]}] , [11, 1, {[1, 3/2]}] .

Здесь 3 – собственное значение , 1 – его кратность, [–2, 1] – собственный вектор.

СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

1) По данной системе Sсформировать матрицу системы и расширенную матрицу системы

>S:=[2*x+3*y+4*z+5*t=6, x+y+z+t+a, x–y+z–t]; задание системы. Отсутствие знака = означает равенство выражения нулю, квадратные скобки можно заменить фигурными

>V:=[x,y,z,t]; список (list) неизвестных.

>genmatrix(S,V); 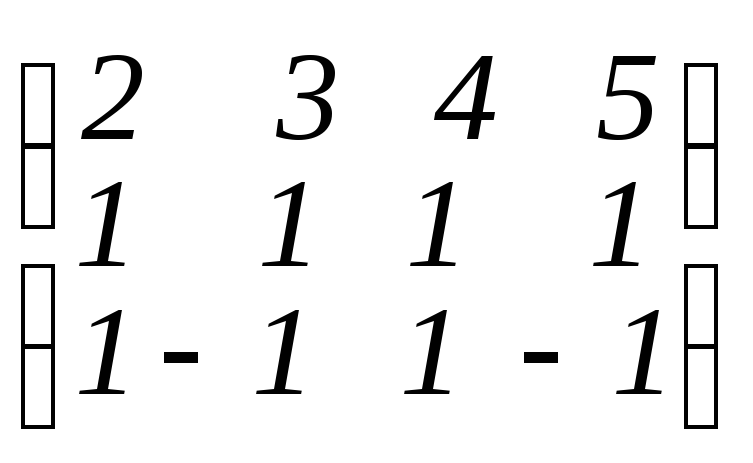матрица системы. Элементы матрицы соответствует порядку неизвестных в списке

>genmatrix(S,V,flag); расширенная матрица системы.

2) По данной матрице А и неизвестным X:=[…] написать однородную систему уравнений

>A:=matrix(2,3,[1,2,3,4,5,6]); >X:=[u,v,w]; Число неизвестных равно числу столбцов!

>geneqns(A,X); ответ: {u+2v+3w=0 , 4u+5v+6w=0}

Если неизвестные не задавать, то команда

>geneqns(A,z); составляет систему {z₁+2z₂+3z₃=0 , 4z₁+5z₂+6z₃=0}

Если задать ещё вектор b правых частей, то можно составить неоднородную систему

>b:=vector([7,8]); Число координат вектораbравно числу строк!

>geneqns(A,x,b); ответ: {4x₁+5x₂+6x₃=8 , x₁+2x₂+3x₃=7}

3)Нахождение общего решения (с параметрами x1,x2,x3, …) для системы линейных уравне­ний с заданной расширенной матрицей Аступенчатоговида

>X:=backsub(A,false,x); (вместох можно использовать другую букву)

Пример.

>A:=matrix(2, 5, [1,2,3,4,10,0,0,1,2,3]);

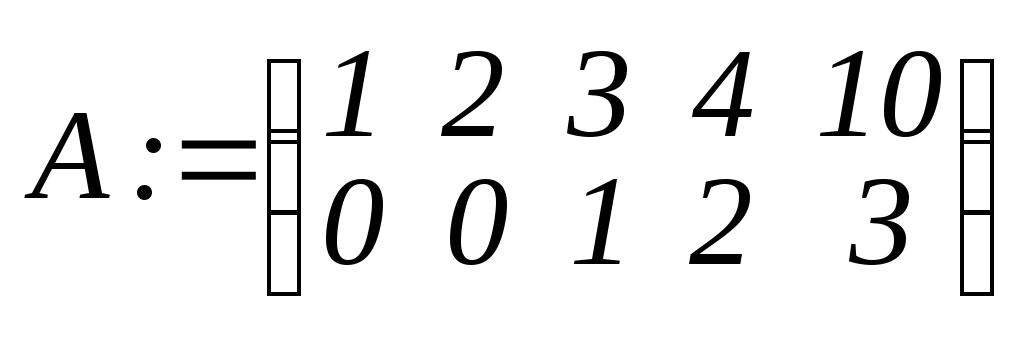
>P:=backsub(A,false,x); P: = [–2x₂+2x₁+1 , x₂ , –2x₁+3 , x₁].

Для получения какого-нибудь частного решения нужно придать свободным неизвестным (т.е. параметрам x[1] ,x[2]) какие-нибудь значения, т.е. выполнить, например, команду

>subs(x[1]=1,x[2]=1,%); [1,1,1,1]

Тот же результат можно получить командами

>x[1]:=1:x[2]:=1: [P[n]$n=1..4]; [1,1,1,1]

4) Решение линейной системы Ax=b(здесь векторbзадается без словаvector)

>linsolve(A,b);

Если система несовместна, то нет никакого ответа. При совместности выдается решение сис­темы в параметрическом виде, где параметры имеют неудобный вид _t₁ , _t₂ ,...

>A:=matrix([[1,2,3],[4,5,6],[7,8,9]]);

>b:=[6,15,24];

>linsolve(A,b); Ответ: [_t₁ 3–2_t₁ _t₁]

К сожалению, с такими параметрами нельзя использовать команду subs(...) (см. предыдущий пример) для получения частного решения. Поэтому эту команду лучше применять для случая, когда существует единственное решение системы. В данном же случае для решения системы следует использовать команду

>linsolve(A,b,’r’,u); [u₁3–2u₁u₁] общее решение с параметромu₁

>subs(u[1]=2,%); [2 –1 2] частное решение

5) Матричное уравнение АХ=В решается такой же командой >linsolve(A,В);

Для решения матричного уравнения ХА=В нужно решить командой linsolveтранспониро­ванное уравнение А^ТХ^Т=В^Т и затем транспонировать результат. Если матрицы А и В квадрат­ные, то уравнение ХА=В решается командой >X:=evalm(B/A); а уравнение АХ=В решается командой >X:=evalm(1/A&*B);

6) Решение переопределенной системы Ах = bпо методу наименьших квадратов

>A:=matrix(3, 2, [2,3,1,1,1,–1]); 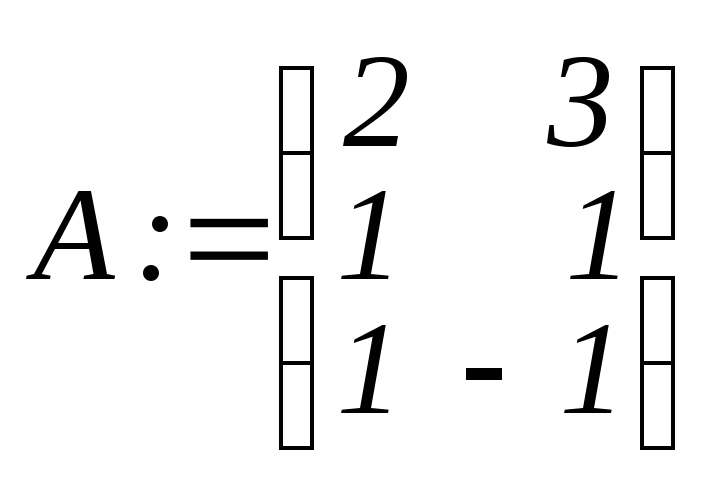задание матрицы А системы уравнений.

>b:=[4,2,3]; задание правых частей векторомb(можно без словаvector),

>leastsqrs(A,b); нахождение решения системы, ответ: [77/30, –2/5].

ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ

1) Вычисление ротора векторного поля

>F:=[x*y,y*z,z*x]; задание пространственного векторного поля,

>u:=[x,y,z]; задание переменных, по которым будет вычисляться ротор,

>rotF:=curl(F,u); вычисление ротора, ответ:rotF:=[–y,–z,–x].

2) Вычисление дивергенции векторного поля

>F:=[x*y,y*z,z*x]; задание пространственного векторного поля,

>u:=[x,y,z]; задание переменных, по которым будет вычисляться дивергенция,

>divF:=diverge(F,u); вычисление дивергенции, ответ:divF: =y+z+x

3) Вычисление градиента скалярной функции

>F:=x*y*z; задание скалярной функции,

>V:=[x,y,z]; задание переменных, по которым будет вычисляться градиент,

>gradF:=grad(F,V); вычисление градиента, ответ:gradF: = [yz,zx,xy].

4) Матрица Вронского от функций f(x),g(x),h(x) находится по команде

>A:=Wronskian([f(x), g(x), h(x)],x);

Определитель Вронского вычисляется затем по команде >det(A);

5) Оператор Лапласа от данной функции F(x,y,z)по данным переменным[x,y,z]

>laplacian(F(x,y,z),[x,y,z]);

6) Якобиан от данной системы функций [ u(x,y,z) , v(x,y,z) , w(x,y,z)] по переменным[x,y,z]

>jacobian([u(x,y,z) , v(x,y,z) , w(x,y,z)] , [x,y,z]);

7) Нахождение потенциала векторного поля.

>f: = [P(x,y),Q(x,y)]; – задание векторного поля,

>potential(f, [x,y],’F’); – проверка поля на потенциальность (true,false) и вычисление

потенциала Fвекторного поляf,

>F; – вывод потенциала на экран.

Аналогичным образом находится потенциал для трехмерного поля.

>f:=[P(x,y,z),Q(x,y,z),R(x,y,z)];

>potential(f, [x,y,z], ‘F’);

>F;

ЛИНЕЙНЫЕ СТРУКТУРЫ НА ПЛОСКОСТИ

Задание точки.

Точка на плоскости задается двумя координатами в квадратных скобках

>a:=[3, 5];B1:=[–5, 2/3]; и т.д.

Названия точек – это произвольные сочетания букв и цифр. Запрещены названия D,I,O. Вместо них можно писатьd,i,o. Координаты точек должны быть рациональными или десятичными. Запрещены координаты типа,ln(5) . Следует писать в таких случаях,ln(5.0).

Точка наносится на плоскость в виде кружочка командой

>PLOT(POINTS(a, B1, [2, 3]), OPTIONS);

Здесь a, В1 – ранее заданные точки, [2, 3] – точка, которая ранее не была определена.

Цвет точки определяется опцией COLOR(HUE,n), где числоп задает цвет положением на «радужной» шкале

красный оранжевый желтый зелёный голубой синий фиолетовый малиновый

n= 0.0 0.1 0.15 0.3 0.45 0.6 0.8 0.9

Примечание. Можно сначала заранее задать множество точек командой

>W:=POINTS(a,B1, [2, 3]);

а уже затем нанести их на плоскость командой

>PLOT(W);

ПРИМЕЧАНИЕ. Опции точки (цвет,форма) и других объектов можно заранее не задавать, а щелкать по объектам правой мышью и выбирать опцию из появившейся таблицы.

Ломаная линия.

Ломаная линия задается командой

>P:=CURVES([a,b,c,d]); гдеa,b,c,d– ранее заданные точки.

На плоскость ломаная линия наносится командой

>PLOT(P,OPTIONS);

В качестве опций можно рассматривать толщину линии – THICKNESS(n). Чем большеп, тем больше толщина ломаной. Наряду с опцией цветаCOLOR(HUE,n) можно определять цвет, задавая интенсивности цветов: красного (r), зеленого (g), синего (b) –COLOR(RGB,r,g,b).

Примечание. Можно сразу задать несколько ломаных

>P:=CURVES([a,b,c,d], [p,q,r,s]);

а затем построить их одной командой.

>PLOT(P,OPTIONS);

Многоугольник (замкнутая ломаная линия).

Пусть заданы точки a,b,c,d. Тогда многоугольник, образованный отрезками [a,b], [b,c], [c,d], [d,a] задается командой

>Q:=POLYGONS([a,b,c,d]);

На плоскости этот многоугольник рисуется командой

>PLOT(Q,OPTIONS);

Граница многоугольника рисуется черным цветом, толщина границы задается опцией THICKNESS(n). Опция цвета дает заливку многоугольника этим цветом, границы остаются черными.

Этот же многоугольник можно нарисовать командой

>PLOT(CURVES([a,b,c,d,a]), OPTIONS);

В этом случае опция цвета не дает заливку, а раскрашивает только границу многоугольника.

Примечание. Можно сразу задать несколько многоугольников

>Q:=POLYGONS([a,b,c], [p,q,r,]);

а затем построить их одной командой.

>PLOT(Q,OPTIONS);

Надпись в данной точке.

Текст “KANT” в точке [3, 5] задается командой

>R:=TEXT([3, 5],KANT,OPTIONS);

После этого текст наносится на плоскость командой

PLOT(R);

В качестве опций можно брать опцию цвета надписи, а также опции горизонтального и вертикального выравнивания текста:

ALIGNLEFT,ALIGNRIGHT– надпись слева или справа от точки

ALIGNABOVE,ALIGNBELOW– надпись сверху или снизу от точки.

Опции горизонтального и вертикального выравнивания можно применять одновременно

Совмещение объектов на одном рисунке.

Ранее заданные объекты P,Q,Rсовмещаются на одном рисунке командой

>PLOT(P,Q,R);

ЛИНЕЙНЫЕ СТРУКТУРЫ В ПРОСТРАНСТВЕ

Задание точки.

Точка в пространстве задается тремя координатами в квадратных скобках

>a:=[3, 5, –1];B1:=[–5, 2/3, 0]; и т.д.

Названия точек – это произвольные сочетания букв и цифр. Запрещены названия D,I,O. Вместо них можно писатьd,i,o. Координаты точек должны быть рациональными или десятичными. Запрещены координаты типа,ln(5) . Следует писать в этом случае,ln(5.0).

Точка наносится на плоскость в виде кружочка командой

>PLOT(POINTS(a, B1, [2, 3,5]), OPTIONS);

где a, В1 – ранее заданные точки, [2, 3, 5] – точка, которая ранее не была определена.

Отрезки определяются двумя точками.

Множество отрезков задается командой

>P:=CURVES([a,b],[c,d],[e,f]);

Затем эти отрезки строятся в пространстве командой

>PLOT3D(P,OPTIONS);

Многоугольники.

Множество многоугольников определяется командой

>Q:=POLYGONS([a,b,c],[p,q,r]);

Затем эти многоугольники строятся в пространстве командой

>PLOT3D(Q,OPTIONS);

Совмещение объектов на одном рисунке.

PLOT3D(P, Q, OPTIONS);

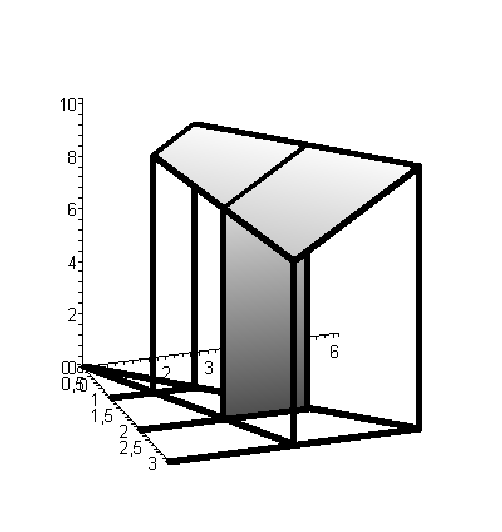
Задача. Построить плоскостьz=10 – 2x + y над областью {1 ≤ x ≤ 3 , x  y  2x } и сечение соответствующей усеченной призмы плоскостьюх = 2.

> a:=[1,0,0]:b:=[2,0,0]:c:=[3,0,0]:

a1:=[1,1,0]:b1:=[2,2,0]:c1:=[3,3,0]:

a2:=[1,2,0]:b2:=[2,4,0]:c2:=[3,6,0]:

A1:=[1,1,9]:B1:=[2,2,8]:C1:=[3,3,7]:

A2:=[1,2,10]:B2:=[2,4,10]:C2:=[3,6,10]:o:=[0,0,0]:

> P:=CURVES([o,c1],[o,c2],[a,a2],[b,b2],[c,c2],

[a1,A1],[a2,A2],[c1,C1],[c2,C2]):

> Q:=POLYGONS([A1,A2,C2,C1],[b1,B1,B2,b2]):

> PLOT3D(P,Q,THICKNESS(4),COLOR(RGB,0,0,1));

plottools – пакет для изображения некоторых геометрических объектов

подгрузка пакета >with(plottools):

1. Дуга окружности с центром в точке (Xc, Yc) , радиуса R, охватывающая угол ().

>L:=arc([Xc,Yc],R,..): задание дуги.

>plots[display](L,options); изображение этой дуги

Примечание. Если произвести ещё подгрузку with(plots), то вместо последней команды можно выполнить команду

>display(L,options);

Другие объекты изображаются аналогично.

2. Окружность с центром в точке (Xc, Yc) , радиуса R.

>C:=circle([Xc,Yc],R): задание окружности.

>plots[display](C,options); изображение этой окружности

Примечание. Если произвести ещё подгрузку with(plots), то вместо последней команды можно выполнить команду

>display(С,options);

3. Конус с вершиной и точке (a,b,c), с радиусом основания R и высотой Н (возможно H<0) .

>C:=cone([a,b,c],R,H): задание конуса.

>plots[display](C,options); изображение этого конуса.

Примечание. Если произвести ещё подгрузку with(plots), то вместо последней команды можно выполнить команду

>display(С,options);

4. Отрезок между точками А(a1,a2) , B(b1,b2)

>L:=line([a1,a2] , [b1,b2]): задание отрезка.

>plots[display](L,options); изображение этого отрезка.

Примечания. а)Если произвести ещё подгрузку with(plots), то вместо последней команды можно выполнить команду

>display(L,options);

б) Если точки задаются тремя координатами, то отрезок изображается в пространстве.

5. Многоугольник ABCD

P:=polygon([[a1,a2],[b1,b2],[c1,c2],[d1,d2]]): задание многоугольника.

>plots[display](Р,options); изображение этого многоугольника.

Примечания. а)Если произвести ещё подгрузку with(plots), то вместо последней команды можно выполнить команду

>display(Р,options);

б) Если точки задаются тремя координатами, то многоугольник изображается в пространстве.

в) Опция color дает цвет заливки многоугольника.

6. Точки A(a1,a2), B(b1,b2)

>P:=point([a1,a2],options), point([b1,b2],options): задание точек. В качестве опций можно задавать

цвет (color=...) , форму точки (symbol=circle, box, diamond) , размер точки (symbolsize=30).

>plots[display](P); изображение этих точек.

Примечание. Если произвести ещё подгрузку with(plots), то вместо последней команды можно выполнить команду

>display(Р);

Если заданы несколько объектов, то они изображаются командой

>plots[display]([P,Q,L]);

Другте фигуры см. в пакете plottools.