2 Семестр, вариант – 13

1. Для функции проверить справедливость теоремы Шварца.

2. В уравнении сделать замену переменных.

3. Функция y(x) удовлетворяет функциональному уравнению x⁵y⁴+7x–x³y⁵+2y+1 = 0. Найти y’(x) и написать уравнение касательной к графику этой функции в точке его пересечения с осью Х.

4. Написать уравнение касательной плоскости к графику функции в точке (1, 1). Вычислив дифференциал функции, найти её приближенное значение в точке

(0,98; 1,04).

К

КАНТ-99

ОНТРОЛЬНАЯ РАБОТА (функции многих переменных)

2 Семестр, вариант – 14

1. Для функции проверить справедливость теоремы Шварца.

2. В уравнении сделать замену переменных.

3. Функция y(x) удовлетворяет функциональному уравнению 5x³y⁴+x+7x⁴y³–2y–6 = 0. Найти y’(x) и написать уравнение касательной к графику этой функции в точке его пересечения с осью Y.

4. Написать уравнение касательной плоскости к графику функции в точке

(3, 4). Вычислив дифференциал функции, найти её приближенное значение в точке

(2,98; 4,04).

К

КАНТ-99

ОНТРОЛЬНАЯ РАБОТА (функции многих переменных)

2 Семестр, вариант – 15

1. Для функции проверить справедливость теоремы Шварца.

2. В уравнении сделать замену переменных.

3. Функция y(x) удовлетворяет функциональному уравнению 4x³y⁴+3x–x²y³+8y+4 = 0. Найти y’(x) и написать уравнение касательной к графику этой функции в точке его пересечения с осью Х.

4. Написать уравнение касательной плоскости к графику функции в точке

(1, 4). Вычислив дифференциал функции, найти её приближенное значение в точке

(0,98; 4,04).

К

КАНТ-99

ОНТРОЛЬНАЯ РАБОТА (функции многих переменных)

2 Семестр, вариант – 16

1. Для функции проверить справедливость теоремы Шварца.

2. В уравнении сделать замену переменных.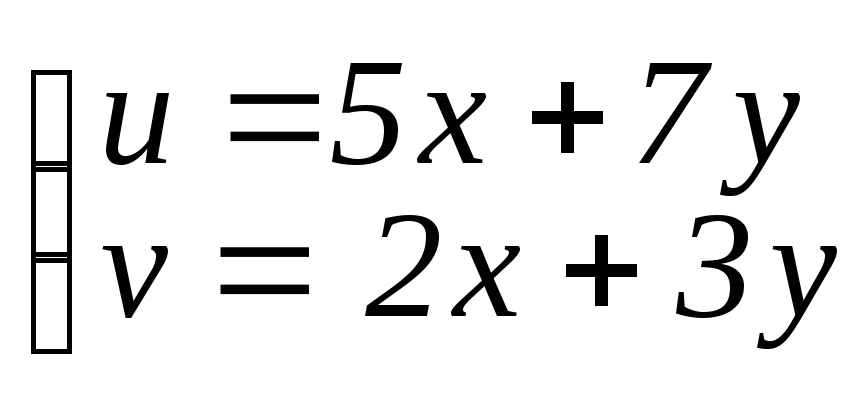

3. Функция y(x) удовлетворяет функциональному уравнению 8x⁵y⁶+7x–x⁶y⁵+8y+9 = 0. Найти y’(x) и написать уравнение касательной к графику этой функции в точке его пересечения с осью Y.

4. Написать уравнение касательной плоскости к графику функции в точке

(1, 3). Вычислив дифференциал функции, найти её приближенное значение в точке

(0,98; 3,04).

К

КАНТ-99

ОНТРОЛЬНАЯ РАБОТА (функции многих переменных)

2 Семестр, вариант – 17

1. Для функции проверить справедливость теоремы Шварца.

2. В уравнении сделать замену переменных.

3. Функция y(x) удовлетворяет функциональному уравнению 6x⁶y⁶+6x–x⁵y⁵–5y+4 = 0. Найти y’(x) и написать уравнение касательной к графику этой функции в точке его пересечения с осью Х.

4. Написать уравнение касательной плоскости к графику функции в точке

(4, 1). Вычислив дифференциал функции, найти её приближенное значение в точке

(3,98; 1,04).

К

КАНТ-99

ОНТРОЛЬНАЯ РАБОТА (функции многих переменных)

2 Семестр, вариант – 18

1. Для функции проверить справедливость теоремы Шварца.

2. В уравнении сделать замену переменных.

3. Функция y(x) удовлетворяет функциональному уравнению 3x³y³+2x+x⁴y⁴–9y+4 = 0. Найти y’(x) и написать уравнение касательной к графику этой функции в точке его пересечения с осью Y.

4. Написать уравнение касательной плоскости к графику функции в точке

(9, 4). Вычислив дифференциал функции, найти её приближенное значение в точке

(8,98; 4,04).

К

КАНТ-99

ОНТРОЛЬНАЯ РАБОТА (функции многих переменных)