(1 Семестр)

ЗАДАЧА 1. Применение формул табличного дифференцирования, которые, конечно же, надо знать наизусть.

ЗАДАЧА 2. Левая часть уравнения. Продифференцировать данную функцию и подставить полученную производную в левую часть уравнения.

Правая часть уравнения. Подставить данную функцию в правую часть уравнения (определитель ). Убедиться, что левая часть равна правой.

ЗАДАЧА 3. Асимптотическая формула линеаризации для функции y=f(x) в точке х₀ имеет вид f(x)=f(x₀)+f’(x₀)(x–x₀)+o(x–x₀) , x x₀ . Из нее легко получаются уравнение касательной у_кас = f(x₀)+f’(x₀)(x–x₀) в точке х=х₀ , и приближенная формула линеаризации f(x)  f(x₀)+f’(x₀)(x–x₀) при х х₀ , которая используется для приближенного вычисления значения функции при х  х₀ .

ЗАДАЧА 4. Определение. Дифференциалом функции y=f(x) на отрезке [x, x+x] называется величина dy=f’(x)x. Эта величина характеризует погрешность функции y=f(x) при заданной погрешности х аргумента.

Пусть дана функция . Найдем её значение прих=2 0,001.

Вычисляем основное значение функции при х=2. Получаем у=1. Для вычисления погрешности этой величины находим дифференциал и подставляем сюдах=2, х=0,001. Получим dy=0,006. Это и есть погрешность значения функции. Ответ: Значение функции в точке х=2 0,001 равно у=10,006.

Примечание. Знак означает, что если у аргумента х мы ошибаемся в большую сторону, то у функции у мы ошибаемся в меньшую сторону

ЗАДАЧА 5. Для вычисления предела нужно произвести линеаризацию (см. задачу 3) числителя и знаменателя в точке, к которой стремится х.

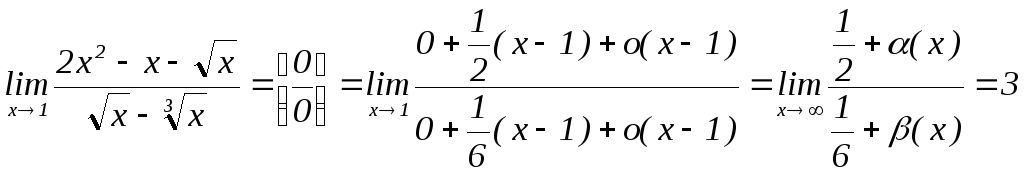
Примечание. Если группа плохонькая, то вместо АФЛ можно пользоваться приближенной формулой линеаризации (без о-малого).

ДР-3. Полное исследование функции с построением графика.

(1 Семестр)

План исследования.

1. Исследование ФУНКЦИИ, т.е. нахождение области определения, точек пересечения с осями, определение знака, исследование поведения на бесконечности и в точках разрыва, нахождение асимптот. Если имеются бесконечные разрывы, то при построении графика с помощью MAPLE обязательно делать ограничения по оси Y (опция y=a..b ), а также применять опцию discont=true.

2. Исследование 1-й ПРОИЗВОДНОЙ. При помощи MAPLE найти корни 1-й производной командой >solve(diff(f(x),x),x);.Добавить к ним точки, в которых производная не существует. Отложить все эти точки на прямой и определить знак производной в промежутках между точками. Изобразить стрелочками интервалы монотонности, указать точки экстремума и найти значения функции в этих точках.

3. Исследование 2-й ПРОИЗВОДНОЙ, т.е. нахождение интервалов выпуклости и вогнутости, а также точек перегиба. Для нахождения корней 2-й производной можно пользоваться командой >solve(diff(f(x),x,х),x);

4. Нахождение асимптот.

А) Вертикальные асимптоты. Находим точки, в которых функция не определена, и пределы в этих точках. Если пределы равны бесконечности, то в этих точках имеем вертикальные асимптоты.

Б) Горизонтальные асимптоты. Если существует , то прямаяу=Н является ПРАВОЙ горизонтальной асимптотой. Аналогично (при х – ) находим ЛЕВУЮ горизонтальную асимптоту.

В) Наклонные асимптоты. Правая асимптота y=kx+b существует, если существуют два предела: . Аналогично (при х – ) находим ЛЕВУЮ наклонную асимптоту.

5. Построение графика функции с указанием на нем точек экстремума и точек перегиба. Асимптоты (если они существует) строить на этом же графике.

КР-3. Правило Лопиталя, формула Тейлора, асимптотика.