(1 Семестр)

ЗАДАЧА 1. Нахождение производной по определению.

а) Задание функции

> f:=x->(2*x+3)/(4*x+5);

б) Нахождение приращения функции и приведение к общему знаменателю

> dy:=f(x+dx)-f(x);

> dy:=normal(dy); (приведение к общему знаменателю)

в) Нахождение отношения приращений

> dy/dx;

г) Вычисление предела от отношения dy/dx при dx0

> limit(dy/dx,dx=0);

Ответ: Производная данной функции, найденная по определению, равна

Примечание. Эту задачу можно решить и безMAPLE . Если всё же задача решается с применением программыMAPLE , то каждую команду следует сопровождать словесными объяснениями по пунктам а)…г).

ЗАДАЧА 2. Нахождение угла между кривыми.

а) Задание кривых уравнениями

> f:=x->1/x; g:=x->sqrt(x);

б) Нахождение точки пересечения кривых

> x0:=solve(f(x)=g(x),x);

в) Нахождение угловых коэффициентов и запись уравнений касательных для каждой из двух кривых

> k1:=subs(x=x0,diff(f(x),x)); y1:=f(x0)+k1*(x-x0);

> k2:=subs(x=x0,diff(g(x),x)); y2:=g(x0)+k2*(x-x0);

Построение на одном чертеже четырех графиков кривых и касательных к ним. Указать на чертеже искомый угол

> plot({f(x),g(x),y1,y2},x=0.3..2,color=black);

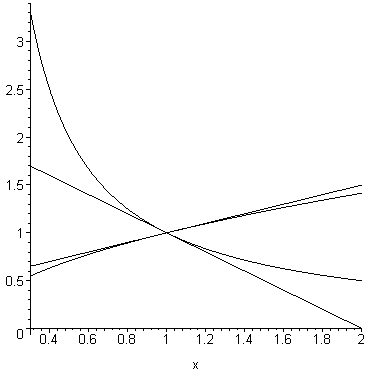
г) Нахождение угла между касательными и перевод этого значения в градусы

> phi:=arctan((k1-k2)/(1+k1*k2));

> evalf(abs(phi)*180/Pi)*degrees;

ЗАДАЧА 3. Определить при каких А и В данная функция является решением данного дифференциального уравнения.

а) Подставляем предполагаемое решение в уравнение.

б) Сокращаем, если нужно на экспоненту.

в) Приравниваем коэффициенты слева и справа при синусах и косинусах либо при одинаковых степенях переменной х.

г) Получаем систему двух уравнений, из которых находим А и В.

д) Пишем ответ: Функция … является решением дифференциального уравнения…

Пример. Определить, при каких значенияхАиВфункцияy = (Ax + B) e^–x является решением дифференциального уравненияy’’– 2y’ + 3y = (12x + 10) e^–x .

Решение. Находим y’ иy” и подставляем их в уравнение. Получим

Сокращая на е^–х и приравнивая коэффициенты прих и свободные члены, получим систему 6А=12 , –4А+6В=10 . Отсюда находим А=2 , В=3 .

Ответ. Решением уравнения является функция y = (2x + 3) e^–x.

Для проверки можно воспользоваться следующими командами пакетаMAPLE

а) Задаем уравнение

> eq:=diff(y(x),x,x)-2*diff(y(x),x)+3*y(x)=(12*x+10)*exp(-x);

б) Задаем предполагаемое решение

> y(x):=(A*x+B)*exp(-x);

в) Определяем, при каких А и В уравнение eq превратиться в тождество

> solve(identity(eq,x),{A,B});

ЗАДАЧА 4. Вычисление пределов ВРУЧНУЮ.

Для вычисления первого предела нужно произвести линеаризацию числителя и знаменателя по формуле f(x)  f(x₀) + f’(x₀)(x – x₀) .

.

Для вычисления второго предела следует воспользоваться эквивалентностями

sin ~  , ln(1+) ~  , exp()–1 ~  , exp()–exp()~ – , (1+)ⁿ–1 ~ n при  .

а также правилом сохранения главных слагаемых

.

Здесь учтено, что приa < 0 .

Результаты вычислений следует проверить на MAPLE командой

>limit(f(x),x=x₀);

ЗАДАЧА 5. Решение уравнения с малым параметром.

Пусть требуется решить уравнение f(x)=(x²+x³)+lnx=0 .Т.к. параметрмал, то первое слагаемое можно отбросить и решать уравнениеlnx=0 , откудах=1 .Это первое приближение корня уравнения. Для получения второго, более точного приближения следует произвести линеаризацию данного уравнения в полученной точкех₀=1. Линеаризация данного уравнения дает уравнение2+(5+1)(х–1)=0 .

Решая это уравнение, найдем приближенное решение исходного уравнения

ЗАДАЧА 6. В данной задаче мы ищем решение уравнения f(x)=0 по методу Ньютона. Для этого мы используем рекуррентную формулу Ньютона. По этой формуле мы, зная начальное приближениех₀найдем более точное приближениех₁. Затем, знаях₁, найдем более точное значениих₂, и т.д.

Возникают два вопроса: а) Где взять начальное приближение х₀ , б) На каком приближении остановиться.

Рассмотрим пример. Пусть требуется найти корень уравнения .

1. Строим график левой части командой

> plot(1/x-ln(x), x=1..2);

2. Выясняем, что на отрезке [1; 2] функция обращается в ноль. Один из концов этого отрезка можно принять за х₀ . Какой?

3. Строим график второй производной и определяем графически её знак – плюс.

4. Определяем, какой из концов отрезка [1; 2] следует взять за х₀ (на него указывает вы­пуклость кривой). В данном случае х₀ = 1.

5. Для определения условия окончания расчета следует задать точность  = 0,000001. Расчет следует продолжать, если разность двух приближений будет больше этого  , и остановить, если

Итак, для расчета по формуле Ньютона мы задаем точность, начальное приближение (обязательно в десятичном виде), функцию и её производную

>eps:=0.000001; x[0]:=1.0;

f:=x->1/x-ln(x); f1:=x->-1/x^2-1/x;

Затем составляем циклическую программу с условием на окончание: «Для п начиная от нуля с шагом 1 до тех пор, пока делать расчет по формуле Ньютона, а затем закончить расчет.

> for n from 0 by 1 while abs(f(x[n])/f1(x[n]))>eps do x[n+1]:=x[n]-f(x[n])/f1(x[n]) end do;

Программа выдаст несколько последовательных приближений для корня уравнения. Последнее принимается за приближенное значение корня данного уравнения.

После получения приближенного значения корня по методу Ньютона вычисляем для проверки точное значение этого корня командой

>fsolve(f(x),x);

ЗАДАЧА 7. Найти точную оценку функции на данном отрезке. Точной оценкой непрерывной функции y=f(x) на отрезке [a,b] называется двойное неравенство m  f(x)  M , где т и М – наименьшее и наибольшее значения функции на данном отрезке (они существуют по 2-й теореме Вейерштрасса).

Найдем оценку функции у=(х³–х²–х+1)е^х на отрезке [–2 ; 1,2]. Для этого

а) Находим критические точки функции командой

> solve(diff((x^3-x^2–x+1)*exp(x),x),x);

б) Выбираем из них точки, лежащие на данном отрезке, т.е. точки х=0 их=1.

в) Вычисляем значения функции в этих точках и на концах отрезка командой подстановки

>subs(x=a,f(x));

г) Из полученных значений выбираем наименьшее т и наибольшееМ.

д) Пишем оценку.

–9е^–2(х³–х²–х+1)е^х 1 для всехх [–2; 1,3].

Примечание. Для проверки можно использовать метод нахождения наибольшего и наименьшего значений функции на данном отрезке при помощи команд

> m:=minimize(f(x),x=a..b);

> M:=maximize(f(x),x=a..b);

е) На одном чертеже строим три графика

> plot({m,f(x),M}, x=a..b);

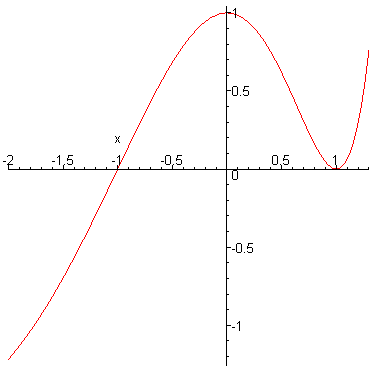
и убеждаемся, что кривая лежит между горизонтальными прямыми (см. рис.).

Что означают слова «ТОЧНАЯ ОЦЕНКА»? Это значит, что расстояние между горизонтальными прямыми нельзя уменьшить.

Точная оценка Просто оценка

ЗАДАЧА 8. Текстовые задачи на экстремум.

В текстовых задачах на экстремум требуется найти максимум или минимум какой-то величины. Для этого эту величину нужно выразить через однупеременную, т.е. представить в виде функции одной переменной, а затем исследовать эту функцию на максимум и минимум.

Задача. Из данного количестваSжести изготовить воронку наибольшего объёма, т.е. найти размеры конуса максимального объема при заданной боковой поверхностиS.

Дано: Боковая поверхность конуса равна ху=S ,гдех – радиус конуса,у –длина образующей. Объем конуса будет равенV=(1/3) x². Из первого условия найдемy=S/x и подставим его во второе равенство. Получим функцию,

, которую нужно исследовать на экстремум.

Ответ: Конус будет иметь наибольший объем при радиусе основания и длине образующей.

КР-2. Табличное дифференцирование, линеаризация, дифференциал.