КР+ДР+MAPLE(1) 13 КАНТ- 2005

КР+ДР+Maple

ОТЧЕТНОСТИ ЗА ПЕРВЫЙ СЕМЕСТР

(инструкция по выполнению)

ФИТ , группы АП-11 и АП-12

КР-1. Элементарные свойства функций. Числовые последовательности.

(1 Семестр)

ЗАДАЧА 1. Графические примеры функций с заданными элементарными свойствами. Использовать «определения».

а) f(x)>0 – график выше оси Х, f(x)<0 – график ниже оси Х.

б) f(x) возрастает – график идет «в гору»,

f(x) убывает – график идет «под гору»,

f(x) не возрастает – график идет «под гору» или горизонтально,

f(x) не убывает – график идет «в гору» или горизонтально.

в) f(x) ограничена сверху – график не поднимается выше прямой у = В,

f(x) ограничена снизу – график не опускается ниже прямой у = А.

г) f(a)=b – график проходит через точку с координатами (a, b).

ЗАДАЧА 2. Построить графики функций с модулями и определить характер монотонности.

Правило. Модуль – это просто скобка, перед которой стоит знак плюс, если величина в скобке  0, и знак минус, если величина в скобке  0.

Сначала расписываем модуль

Пример. y=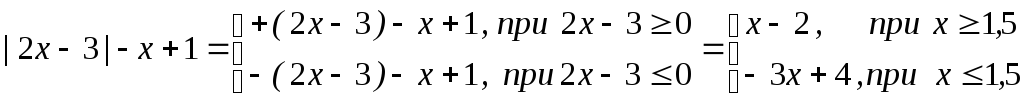

Затем строим график функции у = х – 2 и берем его правее точки х=1,5. На том же чертеже строим график функции у = –3х+4 и берем его левее точки х=1,5 .Построенный график должен быть НЕПРЕРЫВНЫМ (части графика должны «стыковаться»). После построения графика определяем характер монотонности функции, следуя указаниям б) из задачи № 1.

ВНИМАНИЕ!!!

При работе над ошибками по задаче 2 следует расписать каждую из данных функций с модулем на две функции и затем задать функцию, используя команду для кусочно заданной функции

> f:=x->piecewise(x<=1.5,-3*x+4,x–2);

После этого построить график этой функции командой

> plot(f(x),x=-2..3);

и охарактеризовать характер монотонности функции.

ЗАДАЧА 3. Исследовать последовательность на монотонность.

Определения.

Если а_п+1>a_n для любого номера п , то последовательность является возрастающей;

если а_п+1<a_n для любого номера п, то последовательность является убывающей;

если а_п+1 a_n для любого номера п, то последовательность является невозрастающей;

если а_п+1 a_n для любого номера п , то последовательность является неубывающей.

Для выяснения характера монотонности можно применять следующие методы:

а) Найти производную и исследовать её знак: Если а_п' < 0 , то последовательность убывает; если a_n' > 0 , то последовательность возрастает. Примеры

б) Для положительных последовательностей можно рассмотреть величину . Если она больше единицы, то последовательность возрастающая, если меньше единицы – убывающая. Примеры..

в) Знакопеременная последовательность не является монотонной. Примеры.

г) Исследовать знак разности а_п+1 – а_п . Пример. а_п=8п+(–1)^п4 .

Решение. а_п+1–а_п=8(п+1)–(–1)^п4–8п–(–1)^п4=8–(–1)^п80 . Следовательно, последовательность неубывающая.

И ещё два очень «дубовых» метода, для особо «одаренных». Но с ними можно «наколоться».

г) Построить «график» последовательности (это ломаная линия) и по характеру графика («в гору» , «под гору») определить характер монотонности.

д) Составить таблицу значений последовательности и определить характер монотонности по этой таблице.

Исследование на ограниченность.

Определение ограниченности: Если для любого п

a_n  A , то последовательность ограничена СНИЗУ числом А;

a_n  B , то последовательность ограничена СВЕРХУ числом В;

A  a_n  B , то последовательность просто ОГРАНИЧЕНА числами А и В..

Полезные замечания.

а) Возрастающая последовательность всегда ограничена СНИЗУ первым членом.

б) Убывающая последовательность всегда ограничена СВЕРХУ первым членом.

в) Последовательность, имеющая предел, всегда просто ОГРАНИЧЕНА по теореме.

г) Если а_п+ , то она ограничена снизу, если а_п – , то она ограничена сверху.

В прочих случаях полезно рассмотреть график последовательности и убедиться в наличии (или отсутствии) «потолка» либо «пола».

ВНИМАНИЕ!

При работе над ошибками по задаче № 3 следует использовать MAPLE:

Задать последовательность

> a[n]:=f(n);

Вычислить несколько членов последовательности командой

> seq(f(n), n=1..7); или >f(n)$n=1..7;

Построить график последовательности (ломаная линия)

> with(plots):

>listplot([f(n)$n=1..10]);

Сделать выводы.

ЗАДАЧА 4. Доказать данный предел по определению.

Пример. Доказать по определению, что .

Сначала пишем определение (значки  и  не использовать).

Для любого    найдется номер N( ) , начиная с которого (т.е. для всех nN( ) ) будет выполняться неравенство .

Решение задачи Пусть дано произвольное   . Найдем номер N( ) . Для этого решим неравенство . Таким образом для любого    мы нашли номер , начиная с которого выполняется неравенство , что и требовалось доказать.

Примечание. Квадратные скобки [А] обозначают целую часть числа А.

ЗАДАЧА 5. Используя символы о(…) и  , сравнить последовательности.

Для сравнения двух последовательностей a_n и b_n следует найти предел

.

Если L=1, то последовательности эквивалентны, т.е. a_n b_n .

ЕслиL=0, тоa_n=o(b_n) .

Если L= ,то b_n=o(a_n) .

ВНИМАНИЕ!

При работе над ошибками по задаче № 5 следует использовать программу сравнения последовательностей, составленную на языке MAPLE: