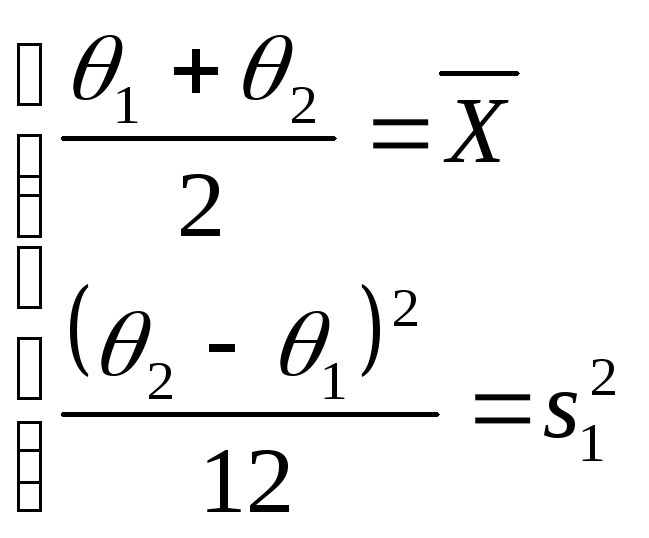Достаточные статистики и оптимальные оценки.
Если для любой оценки
![]() из
класса
из
класса
![]()
![]() ,
для любого
,
для любого
![]() ,
то оценку Т* называют оценкой с
равномерно минимальной дисперсией.
Такая оценка
называется оптимальной
оценкой.
,
то оценку Т* называют оценкой с
равномерно минимальной дисперсией.
Такая оценка
называется оптимальной
оценкой.
Итак, T*
- оптимальная оценка для параметрической
функции
![]() ,
если
,
если
![]() ,
,
![]() ,
,
![]() .
.
Статистика
![]() называется
достаточной
для
параметрического семейства распределений
P=
называется
достаточной
для
параметрического семейства распределений
P=![]() (или
достаточной для параметра
(или
достаточной для параметра
![]() ),
если условный закон распределения
выборки при условии, что статистика
T(X)
приняла некоторое фиксированное значение
t,
не зависит от параметра
),
если условный закон распределения
выборки при условии, что статистика
T(X)
приняла некоторое фиксированное значение
t,
не зависит от параметра
![]() .
.
Теорема Рао-Блекуэлла-Колмогорова: Оптимальная оценка, если она существует, является функцией от достаточной статистики.
Теорема: Если существует полная достаточная статистика, то всякая функция от неё является оптимальной оценкой своего математического ожидания.
То есть оптимальная
оценка однозначно определяется уравнением
![]() ,
где Т – полная достаточная статистика,
H(T)
– произвольная функция от Т.
,
где Т – полная достаточная статистика,
H(T)
– произвольная функция от Т.
Функция
![]() ,
рассматриваемая при фиксированной
реализации выборки
,
рассматриваемая при фиксированной
реализации выборки
![]() как
функция от
как
функция от
![]() ,
называется функцией
правдоподобия.
,
называется функцией
правдоподобия.
Критерий факторизации.
Для того, чтобы
статистика была достаточной для
параметрического семейства распределений
P,
необходимо и достаточно, чтобы функция
правдоподобия выборки
![]() в
нём допускала следующее представление:
в
нём допускала следующее представление:
![]()
Где множитель h(x)
от
![]() не зависит, а функция g(.)
от реализации выборки
не зависит, а функция g(.)
от реализации выборки
![]() зависит
через функцию T(x).
зависит
через функцию T(x).
-
Пусть
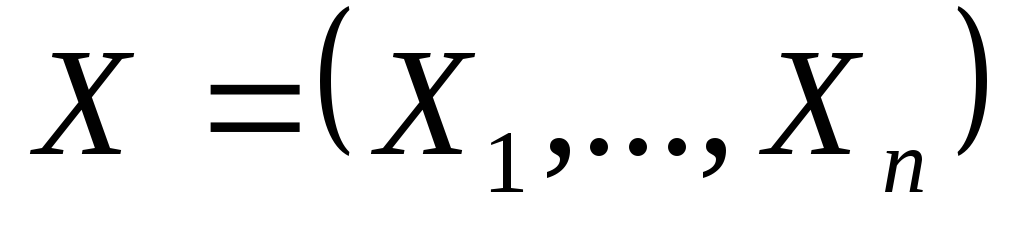 - выборка из распределения
- выборка из распределения
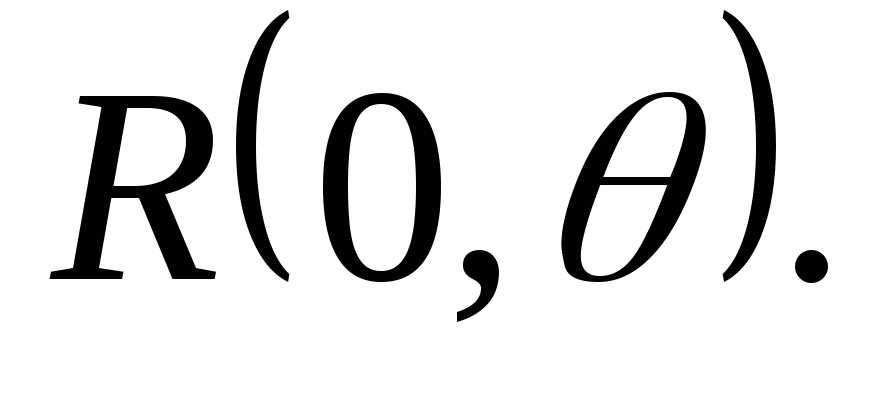 Тогда
Тогда
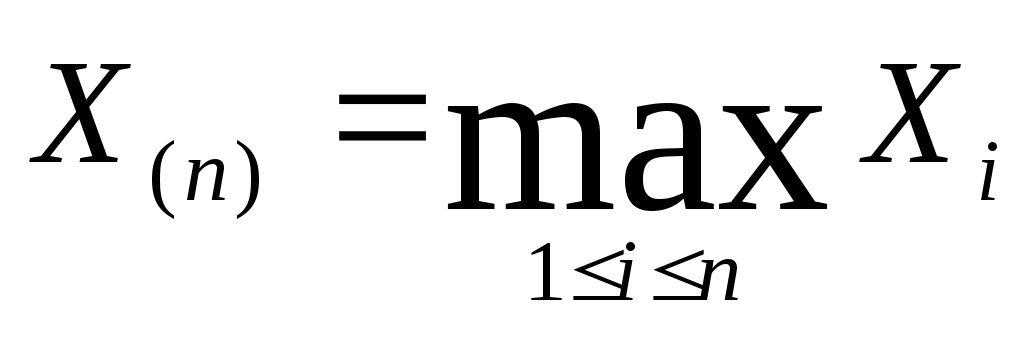 - полная достаточная статистика для
θ. Тогда
- полная достаточная статистика для
θ. Тогда
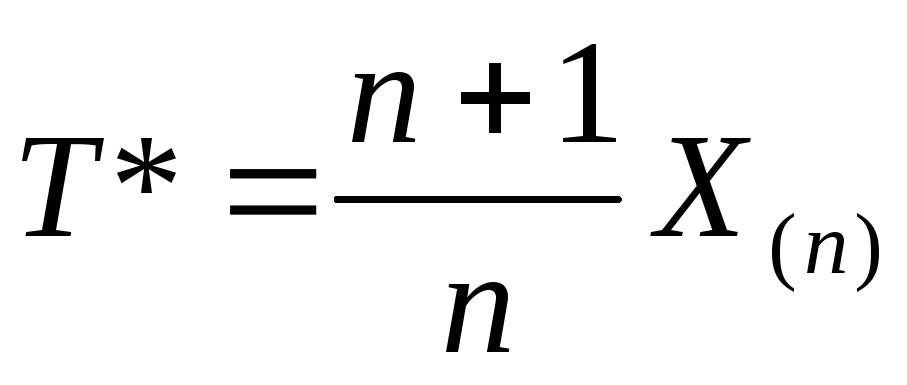 - оптимальная несмещённая оценка θ, и
вообще,
- оптимальная несмещённая оценка θ, и
вообще,
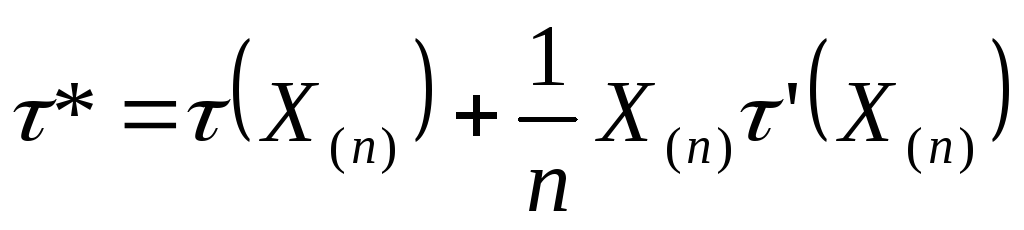 - оптимальная оценка любой дифференцируемой
функции
- оптимальная оценка любой дифференцируемой
функции
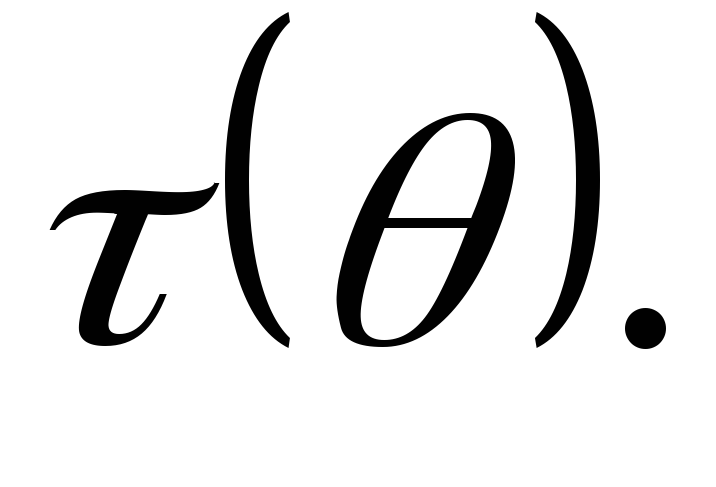
-
Пусть теперь
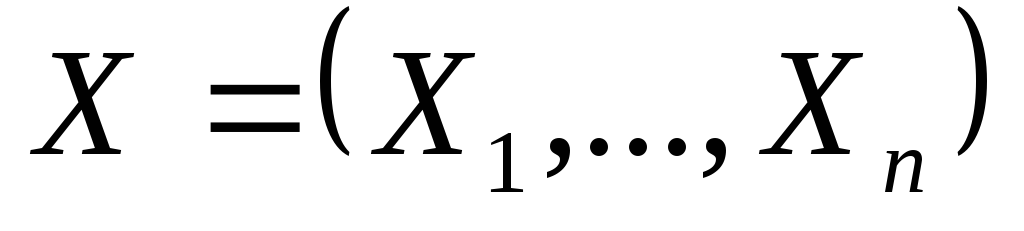 - выборка из распределения
- выборка из распределения
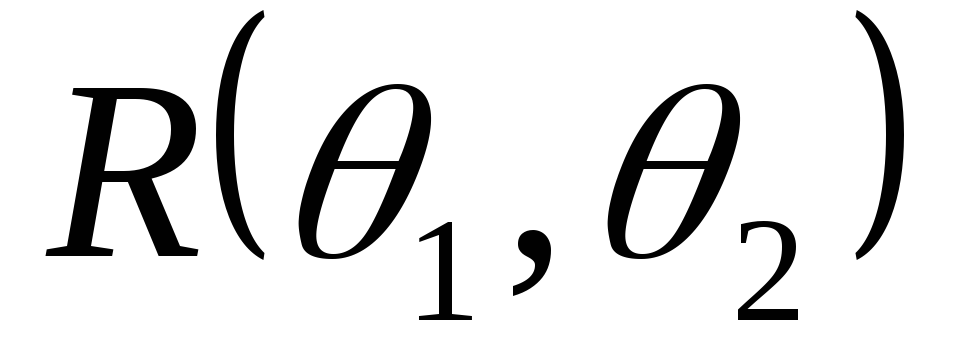 .
Тогда достаточная статистика
.
Тогда достаточная статистика
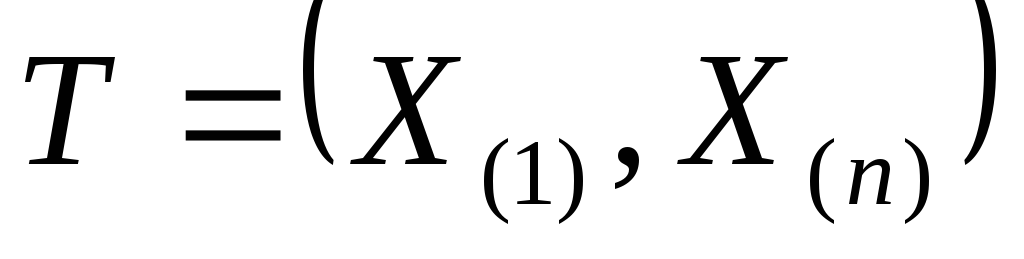 является полной. Кроме того, оценки
является полной. Кроме того, оценки
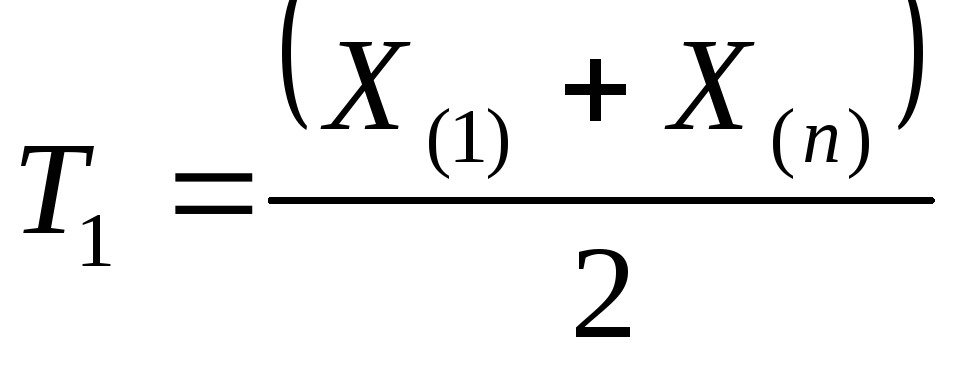 и
и
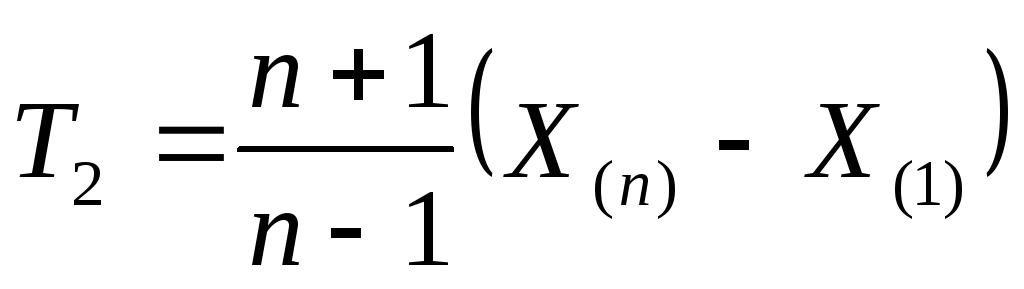 являются оптимальными. Наконец,
статистики
являются оптимальными. Наконец,
статистики
 и
и
 являются
несмещёнными, следовательно, и
оптимальными оценками для параметров
являются
несмещёнными, следовательно, и
оптимальными оценками для параметров
 и
и
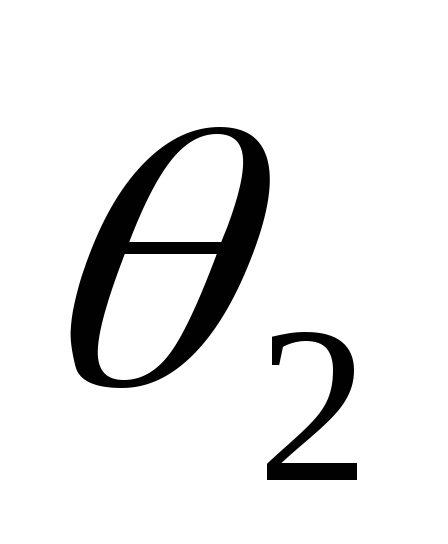 соответственно.
соответственно.
-
Статистика
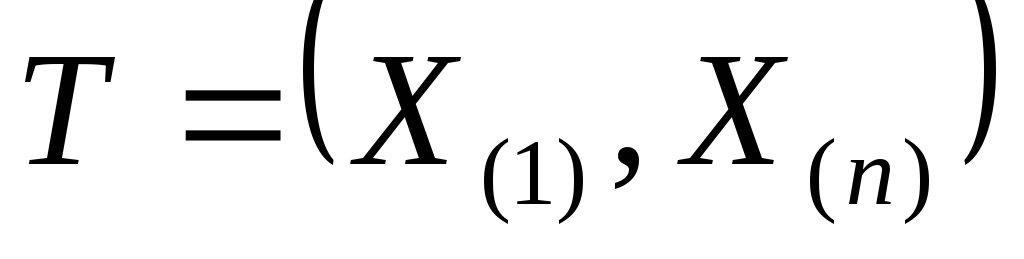 - достаточная для модели
- достаточная для модели
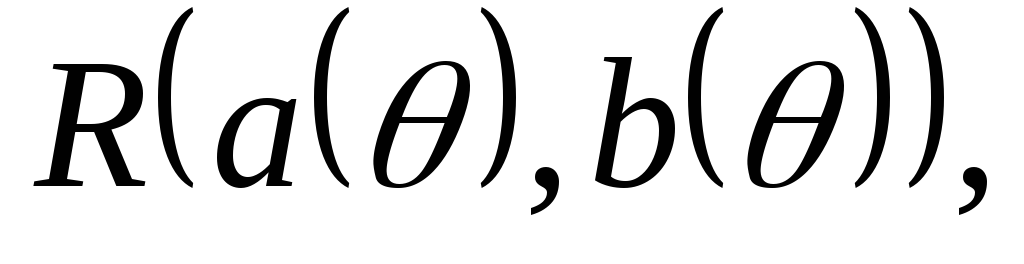 где
где
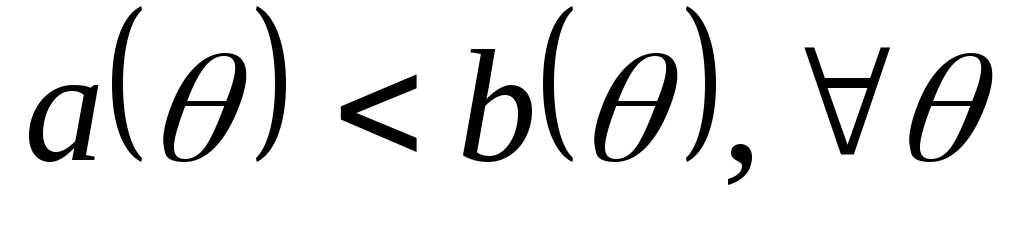 - заданные непрерывные функции скалярного
параметра θ.
- заданные непрерывные функции скалярного
параметра θ.
Если
![]() при
возрастании θ, то в этом случае существует
одномерная достаточная статистика
при
возрастании θ, то в этом случае существует
одномерная достаточная статистика
![]()
Аналогично, если
![]() при
возрастании θ, то одномерная достаточная
статистика существует и имеет вид
при
возрастании θ, то одномерная достаточная
статистика существует и имеет вид
![]()
Этими двумя случаями
исчерпываются ситуации, когда в модели
![]() существует одномерная достаточная
статистика.
существует одномерная достаточная
статистика.
Для модели
![]() достаточной
статистикой является
достаточной
статистикой является
![]() ,
а для моделей
,
а для моделей
![]() и
и
![]() минимальной
достаточной статистикой является T.
минимальной
достаточной статистикой является T.
Оценка методом моменов .
Пусть неизвестный
параметр распределения наблюдаемой
случайной величины
![]() векторный:
векторный:
![]() и у случайной величины
и у случайной величины
![]() существует
конечный r-ый
момент:
существует
конечный r-ый
момент:
![]()
Оценкой неизвестного
параметра
![]() ,
полученной методом моментов (ОММ),
называется вектор
,
полученной методом моментов (ОММ),
называется вектор
![]() ,
где
,
где
![]() есть решение системы
уравнений:
есть решение системы
уравнений:
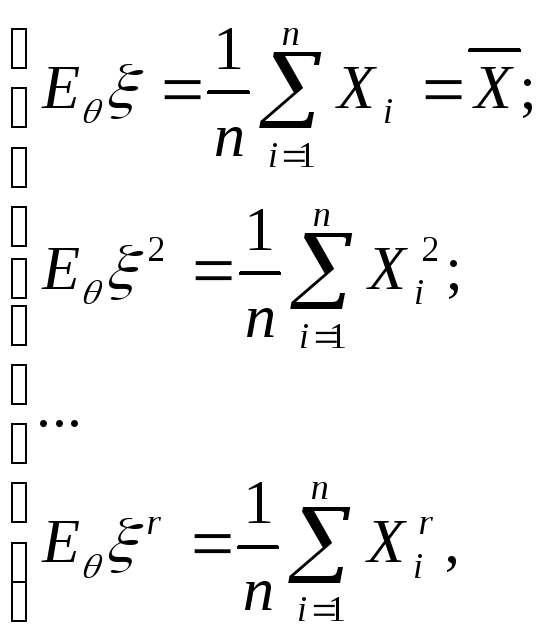
Теоретические
моменты, являющиеся функциями от
неизвестных параметров
![]() ,
приравниваются к
их статистическим аналогам – выборочным
моментам. Полученная система – это
система r
уравнений с r
переменными. Если решения системы
уравнений нет, оценки по методу моментов
не существует. Если имеется несколько
решений, то существует несколько таких
оценок. Если система уравнений имеет
единственное решение, то оценка по
методу моментов является состоятельной
оценкой параметра
,
приравниваются к
их статистическим аналогам – выборочным
моментам. Полученная система – это
система r
уравнений с r
переменными. Если решения системы
уравнений нет, оценки по методу моментов
не существует. Если имеется несколько
решений, то существует несколько таких
оценок. Если система уравнений имеет
единственное решение, то оценка по
методу моментов является состоятельной
оценкой параметра
![]() .
.
-
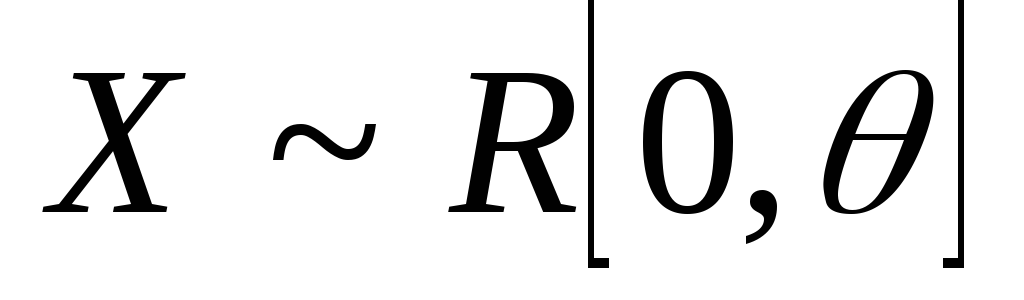
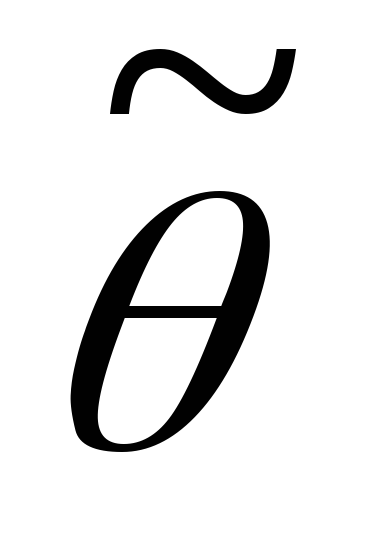 находят
из условия:
находят
из условия:
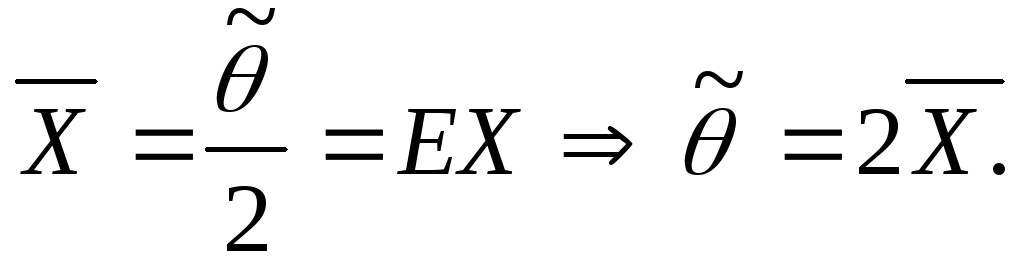
-

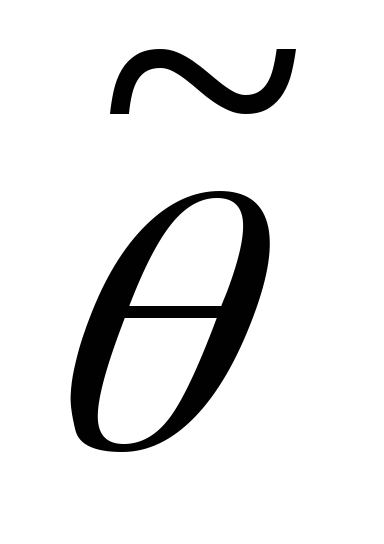 находят из условия:
находят из условия:
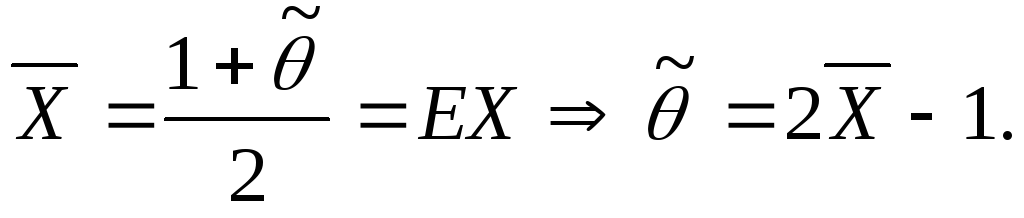
-
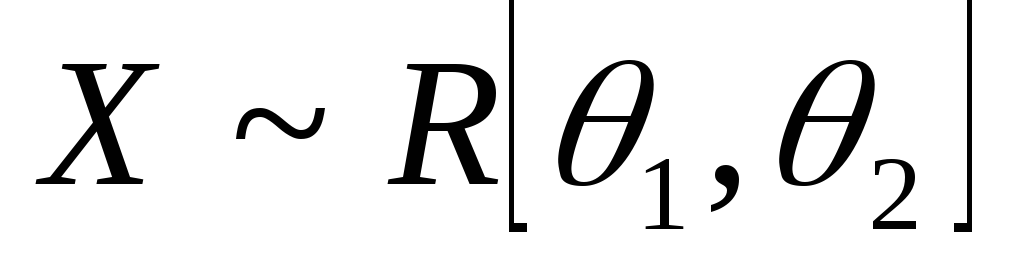
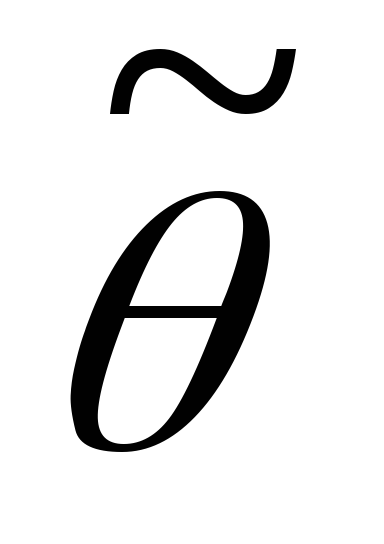 находят
из условий:
находят
из условий: