
Значение
С помощью линейного преобразования приводится к равномерному распределению на отрезке [0,1]. Равномерное распределение является непрерывным аналогом распределений классической теории вероятностей, описывающих случайные эксперименты с равновероятными исходами.
Погрешность, происходящая от округления числа, удовлетворительно описывается равномерным распределением на отрезке [ − 1 / 2,1 / 2].
Если случайная
величина ζ имеет непрерывную функцию
распределения
![]() ,
то случайная величина
,
то случайная величина
![]() имеет равномерное распределение на
отрезке [0,1]. Этим объясняется широкое
использование равномерного распределения
в статистическом моделировании (методы
Монте-Карло).
имеет равномерное распределение на
отрезке [0,1]. Этим объясняется широкое
использование равномерного распределения
в статистическом моделировании (методы
Монте-Карло).
Моделирование
Обозначим буквой
![]() случайную величину с равномерным
распределением на отрезке
случайную величину с равномерным
распределением на отрезке
![]() . Для этой случайной величины функция
распределения и плотность распределения
вероятностей соответственно имеют вид:
. Для этой случайной величины функция
распределения и плотность распределения
вероятностей соответственно имеют вид:
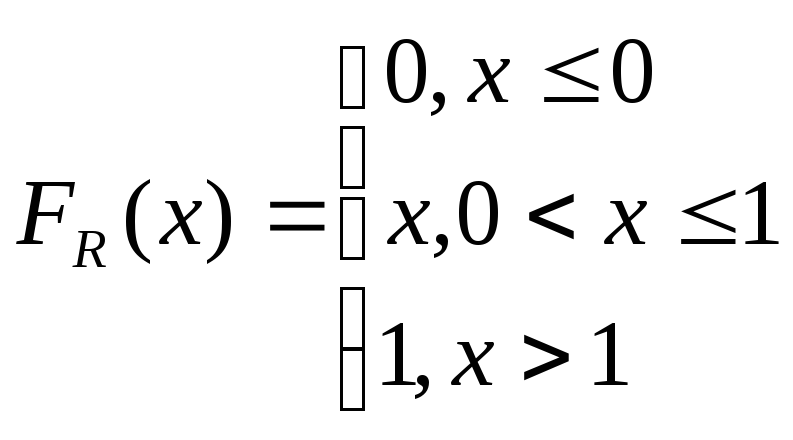
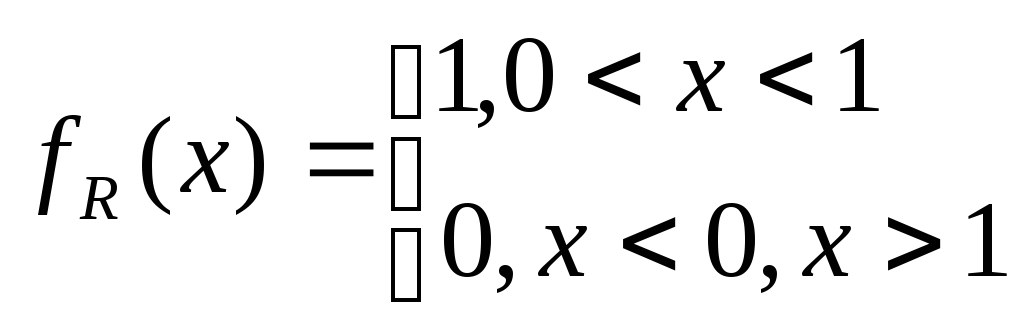
Если
![]()
![]() ,
то вероятность
,
то вероятность
![]()
Моделировать
случайную величину
![]() можно
многими способами.
можно
многими способами.
Мы рассмотрим метод
псевдослучайных последовательностей,
который наиболее просто реализуется в
компьютере. Для получения псевдослучайной
последовательности используем алгоритм,
который называется методом середины
квадратов. Поясним его на примере.
Возьмем некоторое число
![]() .
Пусть
.
Пусть
![]() Возведем его в квадрат:
Возведем его в квадрат:
![]() .Выберем
четыре средние цифры этого числа и
положим
.Выберем
четыре средние цифры этого числа и
положим
![]() . Затем возводим
. Затем возводим
![]() в квадрат:
в квадрат:
![]() и снова выбираем четыре средние цифры.
Получаем
и снова выбираем четыре средние цифры.
Получаем
![]() .
Далее находим
.
Далее находим
![]() и т. д. Последовательность чисел
и т. д. Последовательность чисел
![]() принимают за последовательность
значений случайной величины
принимают за последовательность
значений случайной величины
![]() ,
имеющей равномерное распределение на
отрезке
,
имеющей равномерное распределение на
отрезке
![]() . Для оценки степени приближения
последовательности
. Для оценки степени приближения
последовательности
![]() к последовательности случайных чисел
с равномерным распределением используют
статистические критерии.
к последовательности случайных чисел
с равномерным распределением используют
статистические критерии.
Метод обратных функций.
Пусть случайная
величина
![]() имеет
монотонно возрастающую функцию
распределения
имеет
монотонно возрастающую функцию
распределения
![]() .
Известно, что
.
Известно, что
![]() ,
значит, случайная величина
,
значит, случайная величина
![]() с
монотонно возрастающей функцией
распределения
с
монотонно возрастающей функцией
распределения
![]() связана со случайной величиной
связана со случайной величиной
![]() соотношением:
соотношением:
![]()
Отсюда следует, что
значение
![]() случайной
величины
случайной
величины
![]() является
решением уравнения:
является
решением уравнения:
![]() где
где
![]() значение
случайной величины
значение
случайной величины
![]() ,
то есть:
,
то есть:
![]()
Последовательности
значений
![]() случайной
величины
случайной
величины
![]() соответствует
последовательность
соответствует
последовательность
![]() значений
случайной величины
значений
случайной величины
![]() с
функцией распределения
с
функцией распределения
![]() .
.
Моделирование
случайной величины с равномерным
распределением на отрезке
![]()
Пусть случайная
величина
![]() имеет равномерное распределение на
отрезке
имеет равномерное распределение на
отрезке
![]() .
Тогда её
функция распределения имеет описанный
выше вид. Тогда по методу обратных
функций получаем:
.
Тогда её
функция распределения имеет описанный
выше вид. Тогда по методу обратных
функций получаем:
Составляем уравнение
![]() ,
откуда
,
откуда
![]()
Последовательности
значений
![]() случайной величины
случайной величины
![]() соответствует
последовательность значений:
соответствует
последовательность значений:
![]() случайной величины
случайной величины
![]() ,
равномерно распределённой на отрезке
,
равномерно распределённой на отрезке
![]() .
.
Порядковые статистики.
Случайная величина
![]() ,
которая при каждой реализации выборки
,
которая при каждой реализации выборки
![]() принимает значение
принимает значение
![]() ,
называется k-ой
порядковой статистикой.
,
называется k-ой
порядковой статистикой.
Для случая
![]() распределения
порядковых статистик имеют вид:
распределения
порядковых статистик имеют вид:
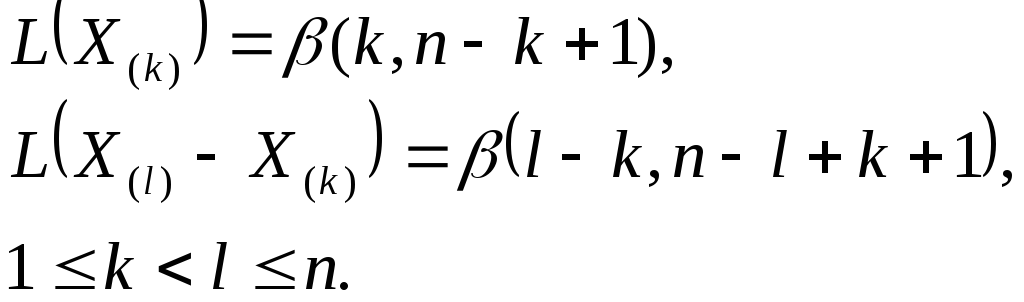
При этом:
![]()
![]()
![]()
![]()
А также:
![]()
Если же
![]() ,
то плотность совместного распределения
экстремальных значений выборки
,
то плотность совместного распределения
экстремальных значений выборки
![]() и
и
![]() имеет
вид:
имеет
вид:
![]()
![]()
А также:
![]()
![]()
![]()
![]()
Отметим далее, что
если
![]() и
и
![]() -
независимые равномерно распределённые
величины на отрезке [0,1], то величины
-
независимые равномерно распределённые
величины на отрезке [0,1], то величины
![]()
![]() - независимы и нормально распределены
с параметрами (0,1).
- независимы и нормально распределены
с параметрами (0,1).
Оценивание параметров в равномерном распределении.
Введём статистический
аналог теоретического математического
ожидания случайной величины
![]() :
:
![]() - выборочное среднее.
- выборочное среднее.
Введём статистический
аналог теоретической дисперсии случайной
величины
![]() :
:
![]() -
выборочная дисперсия.
-
выборочная дисперсия.
Любая измеримая
функция от выборки
![]() называется статистикой.
называется статистикой.
Статистика
![]() называется
несмещённой
оценкой для
заданной параметрической функции
называется
несмещённой
оценкой для
заданной параметрической функции
![]() если
она удовлетворяет условию:
если
она удовлетворяет условию:
![]()
Статистика
![]() для заданной параметрической функции
для заданной параметрической функции
![]() называется
состоятельной,
если
называется
состоятельной,
если
![]()
То есть для любого
![]() при
при
![]()
![]() для любого
для любого
![]() .
.
-
Возьмём выборку
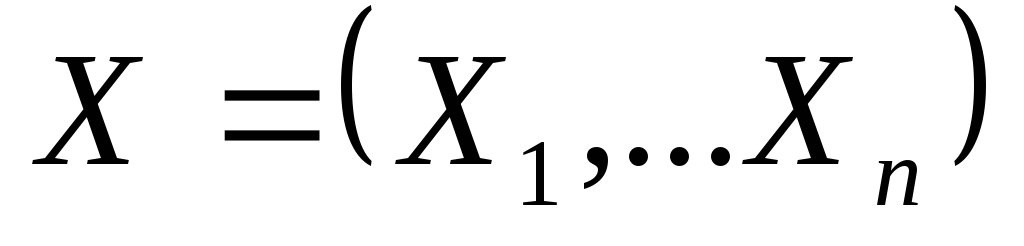 из распределения
из распределения
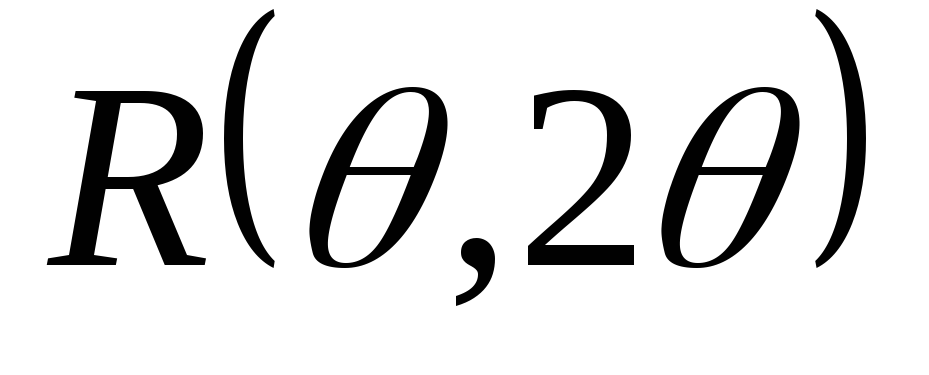 и оценим параметр θ. Рассмотрим класс
оценок вида
и оценим параметр θ. Рассмотрим класс
оценок вида
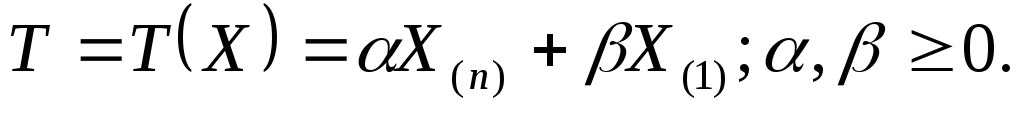
Оптимальной несмещённой оценкой θ в данном классе оценок является:
![]()
Её дисперсия:
![]() .
.
-
Оценим теперь параметр θ равномерного распределения
 по выборке
по выборке
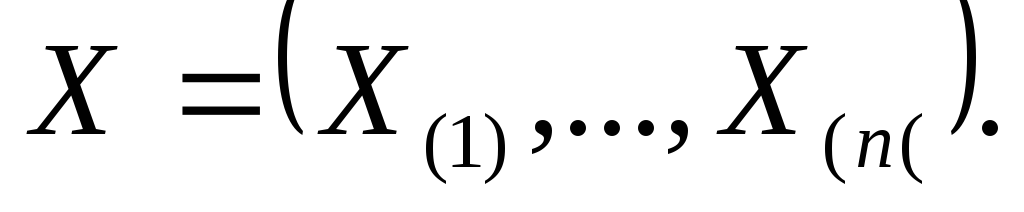 Тогда:
Тогда:
Статистики
![]() и
и
![]() -
несмещённые.
-
несмещённые.
Кроме того, имеем:
![]() то есть оценка
то есть оценка
![]() точнее. Более того,
точнее. Более того,
![]() при
при
![]() то
есть оценка
то
есть оценка
![]() состоятельная.
Оценка же
состоятельная.
Оценка же
![]() не обладает этим свойством.
не обладает этим свойством.
-
Пусть теперь
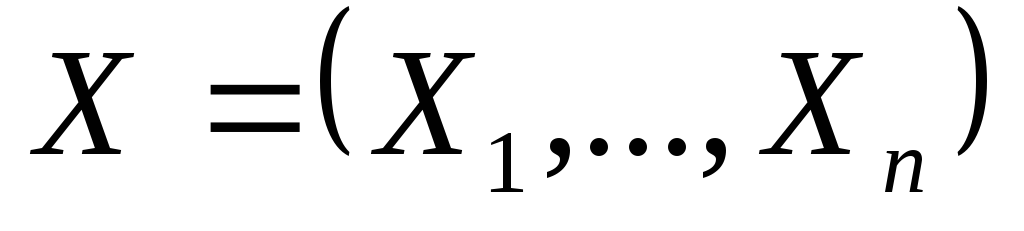 - выборка из
- выборка из
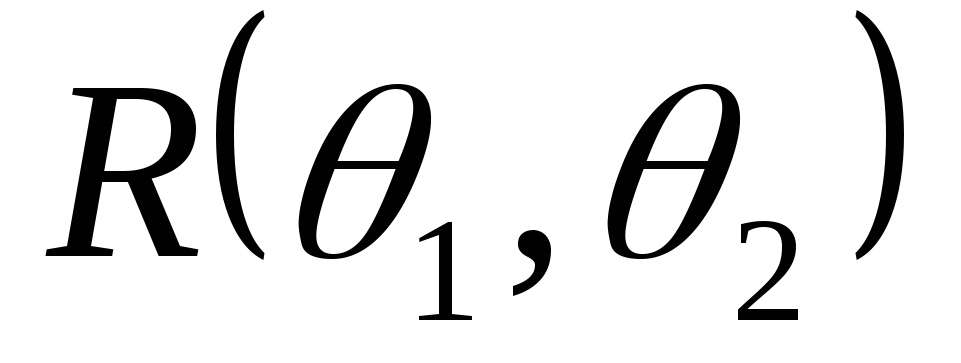 .
Тогда статистики
.
Тогда статистики
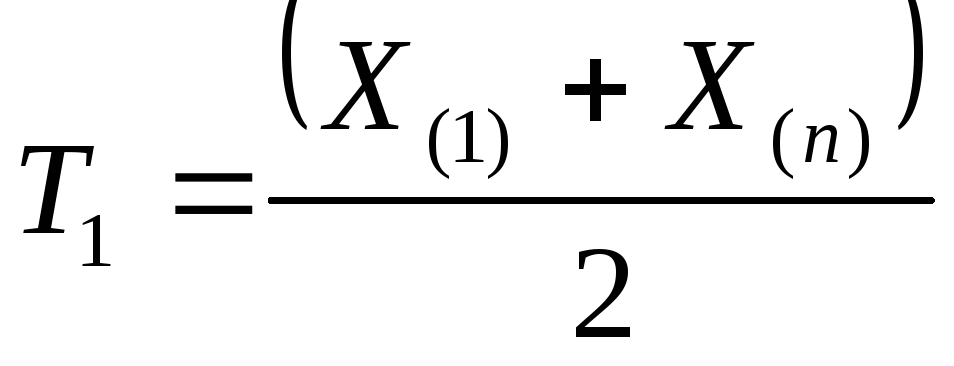 и
и
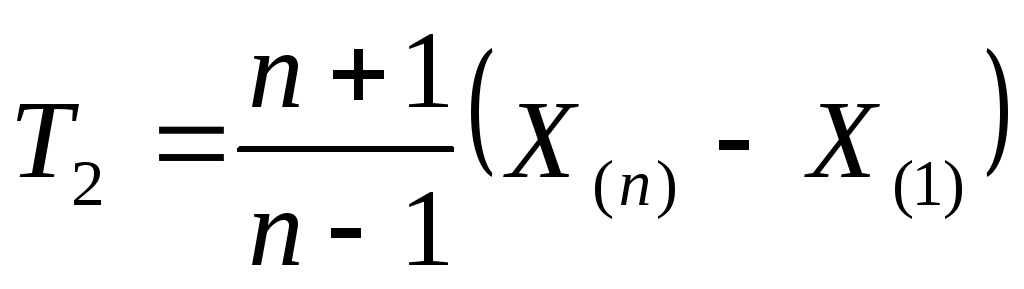 несмещённые и состоятельные оценки
функций
несмещённые и состоятельные оценки
функций
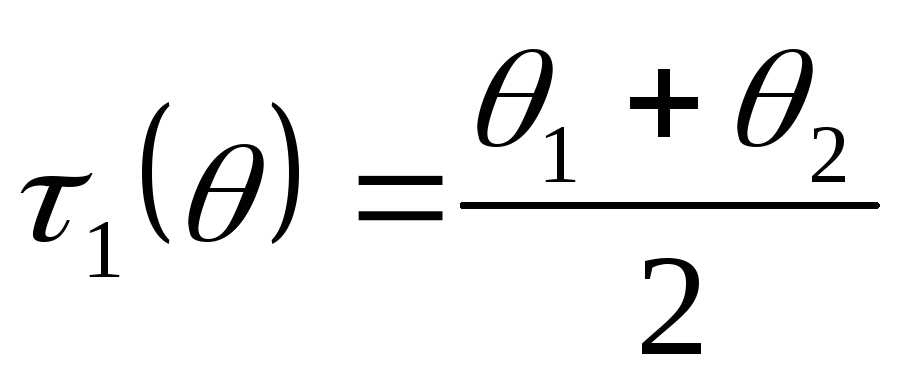 и
и
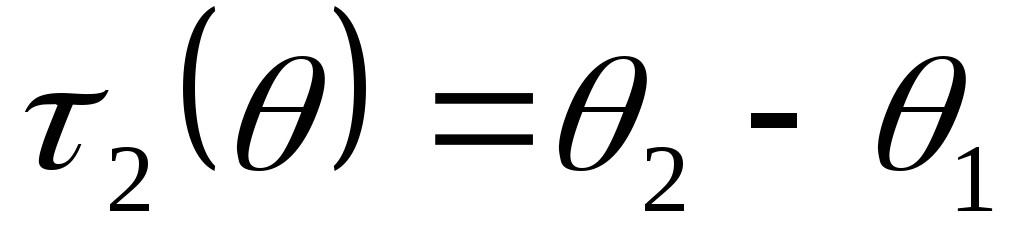 соответственно.
соответственно.
