МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ИНСТИТУТ ЭЛЕКТРОНИКИ И МАТЕМАТИКИ

Кафедра теории вероятностей и математической статистики

РЕФЕРАТ

по математической статистике

на тему:

«Равномерное распределение»

Выполнил: студенты группы М-65

Ражева А.А.

Кнутова А.С.

Проверил: Заведующий Кафедрой

Ивченко Г. И.

Москва 2012 г.

Непрерывное равномерное распределение — в теории вероятностей распределение, характеризующееся тем, что вероятность любого интервала зависит только от его длины.

Равномерное распределение полезно при описании переменных, у которых каждое значение равновероятно, иными словами, значения переменной равномерно распределены в некоторой области.

Определение

Говорят, что случайная величина имеет непрерывное равномерное распределение на отрезке [a,b], где , если её плотность имеет вид:

Пишут: X ~ U (a,b) или

Иногда значения плотности в граничных точках x = a и x = b меняют на другие, например 0 или . Так как интеграл Лебега от плотности не зависит от поведения последней на множествах меры нуль, эти вариации не влияют на вычисления связанных с этим распределением вероятностей.

Если L(ξ) = U(a,b), то

Равномерное распределение U (a,b) описывает процесс «выбора точки наудачу» в интервале [a,b]. Так, если [a,b] – интервал между последовательными отправлениями автобуса от остановки, то время ожидания пассажира, не знающего расписания и пришедшего на остановку, есть случайная величина с распределением U (0,1). Распределение U (0,1) играет особую роль в методах моделирования с помощью компьютеров случайных величин с заранее заданными распределениями. Такие методы широко используют для приближенных вычислений интегралов, решений дифференциальных и интегральных уравнений и т.д.

Пример (Гипотеза случайности).

В некоторых случаях априори предполагается (постулируется), что исходные данные представляют собой случайную выборку из некоторого распределения, т.е. компоненты вектора данных X=(независимы и одинаково распределены. Как правило, это предположение бывает оправдано, так как вытекает из самого характера задачи, и не подвергается сомнению. Но иногда это исходное предположение само нуждается в проверке, т.е. оно рассматривается как статистическая гипотеза , называемая гипотезой случайности. Формализуется такая гипотеза следующим образом. Пусть обозначает функцию распределения выборки , тогда подлежащая проверки гипотеза означает утверждение : , где - некоторая одномерная функция распределения (она может быть полностью задана, либо задано семейство, которому она принадлежит, либо никак не специфицируется). Типичным примером ситуации, когда возникает необходимость проверки гипотезы случайности, является работа генератора (датчика) случайных чисел. Под случайными числами понимается последовательность независимых и равномерно распределённых на отрезке [0,1] случайных величин. Такие числа широко используются в различных областях: в статистике – для моделирования случайных выборок из различных распределений, в криптографии – при получении ключей для шифрования информации, в численном анализе и т.д. В практических задачах последовательность строят либо с использованием готовых таблиц случайных чисел, либо генерируют с помощью специальных датчиков, встроенных непосредственно в ЭВМ, либо получают программным способом по некоторому вспомогательному алгоритму (в последнем случае получаются так называемые псевдослучайные числа т.е. «очень похожие» на случайные). Во всех случаях (особенно в последнем) требуется осуществлять контроль за «качеством» вырабатываемой последовательности (т.е. чтобы эти числа были практически неотличимы от независимых одинаково распределенных чисел), что в математическом плане сводится к проверке гипотезы случайности.

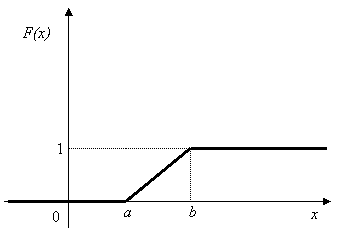
Функция распределения

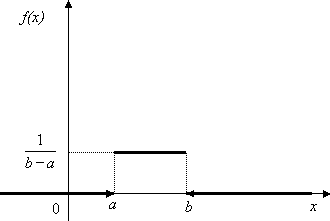
Интегрируя определённую выше плотность, получаем:

Так как плотность равномерного распределения разрывна в граничных точках отрезка [a,b], то функция распределения в этих точках не является дифференцируемой. В остальных точках справедливо стандартное равенство:

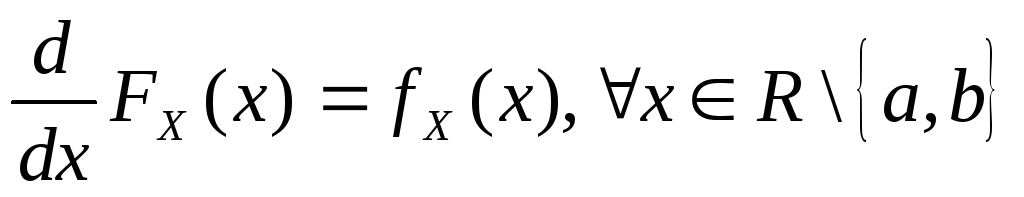
Характеристическая функция случайной величины X ~ U(a,b):

Математическое ожидание и дисперсия по определению равны:

Вообще,

Стандартное равномерное распределение

Если a = 0, а b = 1, то есть X ~ U[0,1], то такое непрерывное равномерное распределение называют стандартным. Имеет место элементарное утверждение:

Если случайная величина X ~ U[0,1], и Y = a + (b − a)X, где a < b, тo Y ~ U[0,1].

Таким образом, имея генератор случайной выборки из стандартного непрерывного равномерного распределения, легко построить генератор выборки любого непрерывного равномерного распределения.

Более того, имея такой генератор и зная функцию обратную к функции распределения случайной величины, можно построить генератор выборки любого непрерывного распределения (не обязательно равномерного) с помощью метода обратного преобразования. Поэтому, стандартно равномерно распределённые случайные величины иногда называют базовыми случайными величинами.

Линейное преобразование

переводит СВ X ~ R(a,b) в СВ Y ~ R(0,1). Действительно,

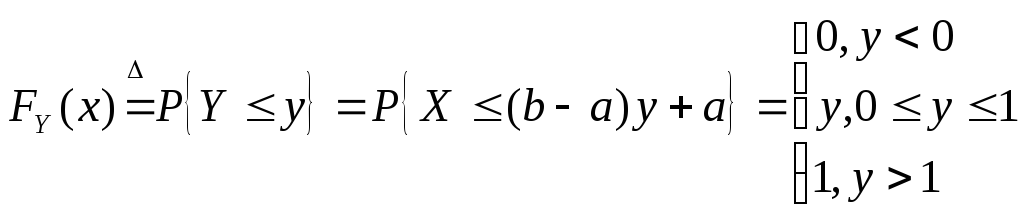
Равномерное распределение является непрерывным аналогом дискретного распределения вероятностей для опытов с равновероятными исходами.