МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
Государственное образовательное учреждение высшего
профессионального образования
«Московский государственный институт электроники
и математики (технический университет)»
Кафедра «Управление и информатика
в технических системах »
ИССЛЕДОВАНИЕ ВРЕМЕННЫХ, ЧАСТОТНЫХ И ЛОГАРИФМИЧЕСКИХ ХАРАКТЕРИСТИК РАЗОМКНУТЫХ И ЗАМКНУТЫХ САУ НА ЭВМ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ЛАБОРАТОРНОЙ РАБОТЕ
по дисциплине
«ОСНОВЫ ТЕОРИИ УПРАВЛЕНИЯ»
Москва 2012
Составители: к.т.н., проф. Казанский И.Н.
к.т.н., доцент Денисова Т.С.
к.т.н., докторант Володин С.М.
Методические указания к лабораторной работе « Исследование времен-
ных, частотных и логарифмических характеристик разомкнутых и замкнутых САУ на ЭВМ » являются составной частью учебно-методического комплекса по дисциплине «Основы теории управления», изучаемой студентами 3 курса специальности 230104 – « Системы автоматизированного проектирования ».
Лабораторная работа выполняется в объеме 8 часов. Студенты проводят исследование временных, частотных и логарифмических характеристик разомкнутой и замкнутой систем автоматического управления (САУ), частотных показателей качества, а также проводят оценку устойчивости САУ с помощью частотных критериев с использованием ЭВМ.
Авторы выражают большую благодарность к.т.н. Тарану А.Н. за предоставленные материалы, которые были использованы в настоящих методических указаниях и при разработке лабораторной работы.
УДК 681.5
Методические указания к лабораторной работе «Исследование временных, частотных и логарифмических характеристик разомкнутых и замкнутых САУ на ЭВМ» по курсу «Основы теории управления», Моск. гос. институт электро-ники и математики; сост. И.Н. Казанский, Т.С. Денисова, С.М. Володин, 2012,
21 с., 19 рис., 1 табл.
СОДЕРЖАНИЕ
|
|
|
Стр. |
|
1. |
Цель лабораторной работы |
4 |
|
2. |
Теоретические сведения |
4 |
|
2.1 |
Частотные характеристики САУ |
4 |
|
2.2 |
Частотные показатели (оценки) качества САУ |
9 |
|
2.3 |
Оценка устойчивости САУ по ее частотным и логарифмическим частотным характеристикам |
12 |
|
3. |
Порядок выполнения лабораторной работы |
16 |
|
4. |
Содержание отчета о лабораторной работе |
20 |
|
|
Литература |
20 |
1. Цель работы
Целью данной лабораторной работы является изучение и исследование студентами временных, частотных и логарифмических характеристик разомкнутой и замкнутой систем автоматического управления (САУ), частотных показателей качества этих систем, а также проведение оценок устойчивости САУ с помощью частотных критериев с применением ЭВМ. Для исследования влияния параметров передаточной функции разомкнутой и замкнутой систем на изменение частотных характеристик, а также на устойчивость систем, в ходе лабораторной работы выполняется моделирование различных характеристик САУ на ЭВМ и расчет соответствующих показателей качества исследуемых систем.
2. Теоретические сведения.
2.1. Частотные характеристики сау
Частотные характеристики обыкновенной линейной САУ (рис.1) могут быть представлены формулами и графиками, характеризующими реакцию системы на гармоническое входное воздействие в установившемся режиме.
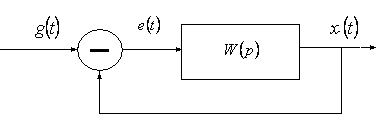
Рис. 1. Обыкновенная линейная САУ
Гармоническое
входное воздействие
- это функция времени, описываемая
линейными комбинациями функций
![]() и
и
![]() .
Если на вход системы подать гармоническое
воздействие
.
Если на вход системы подать гармоническое
воздействие
|
|
(1) |
где
![]() –
амплитуда воздействия;
–
амплитуда воздействия;
![]() - угловая частота воздействия, то на
выходе системы в установившемся режиме
будет также гармоническая функция той
же частоты
- угловая частота воздействия, то на
выходе системы в установившемся режиме
будет также гармоническая функция той
же частоты
![]() ,
но в общем случае сдвинутая по фазе
относительно входной величины на угол
,
но в общем случае сдвинутая по фазе
относительно входной величины на угол
![]() ,
т.е.
,
т.е.
|
|
(2) |
где
![]() -
амплитуда выходной величины;
-
амплитуда выходной величины;
![]() - сдвиг фаз между выходной и входной
величинами.
- сдвиг фаз между выходной и входной
величинами.
Одной
из важнейших характеристик разомкнутой
САУ является ее частотная передаточная
функция (ЧПФ)
![]() ,
которая легко получается из обычной
передаточной функции разомкнутой
системы
,
которая легко получается из обычной
передаточной функции разомкнутой
системы
![]() подстановкой
подстановкой
![]() .
Она
представляет собой комплексное число,
модуль
.
Она
представляет собой комплексное число,
модуль
![]() которого равен отношению амплитуды
выходной величины
которого равен отношению амплитуды
выходной величины
![]() и амплитуде входной величины
и амплитуде входной величины
![]() ,
а аргумент
,
а аргумент
![]() - сдвигу фаз выходной величины по
отношению к входной на каждой частоте
- сдвигу фаз выходной величины по
отношению к входной на каждой частоте
![]() .
.
|
|
(3) |
|
|
(4) |
ЧПФ
![]() может быть представлена в виде:(5)
может быть представлена в виде:(5)
|
|
(5) |
где
![]() и
и
![]() - вещественная и мнимая составляющие
ЧПФ. Для нахождения зависимостей
- вещественная и мнимая составляющие
ЧПФ. Для нахождения зависимостей
![]() ,
,
![]() ,
,
![]() ,
,
![]() используются следующие формулы:
используются следующие формулы:
|
|
(6) |
|
|
(7) |
|
|
(8) |
|
|
(9) |
если
![]() .
Для
наглядного представления частотных
свойств САУ используются следующие
частотные характеристики:
.
Для
наглядного представления частотных
свойств САУ используются следующие
частотные характеристики:
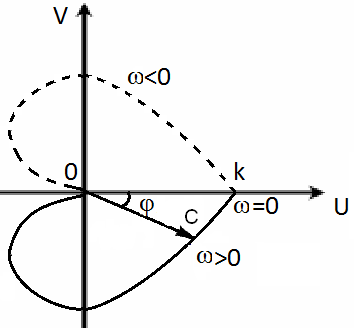
1)
Амплитудно-фазовая
частотная характеристика (АФЧX)
![]() -это кривая, описываемая концом вектора
-это кривая, описываемая концом вектора
![]() на комплексной плоскости U-V
(годограф вектора
на комплексной плоскости U-V
(годограф вектора
![]() )
при изменении частоты входного воздействия
)
при изменении частоты входного воздействия
![]() от -
до +
(рис.2). Длина вектора, проведенного из
начала координат в точку АФЧК,
соответствующую какой-либо выбранной
частоте
от -
до +
(рис.2). Длина вектора, проведенного из
начала координат в точку АФЧК,
соответствующую какой-либо выбранной
частоте
![]() ,
равна модулю
,
равна модулю
![]() ЧПФ.
ЧПФ.
Угол
между этим вектором и положительным
направлением вещественной оси равен
аргументу или фазе
![]() ЧПФ. АФЧХ соответствует выражение (5).
ЧПФ. АФЧХ соответствует выражение (5).
|
|
|
|
|
Рис. 2. Амплитудно-фазовая частотная характеристика |
Рис.3. Амплитудная частотная характеристика |
Рис. 4. Фазовая частотная характеристика |
Амплитудная частотная характеристика (АЧХ)
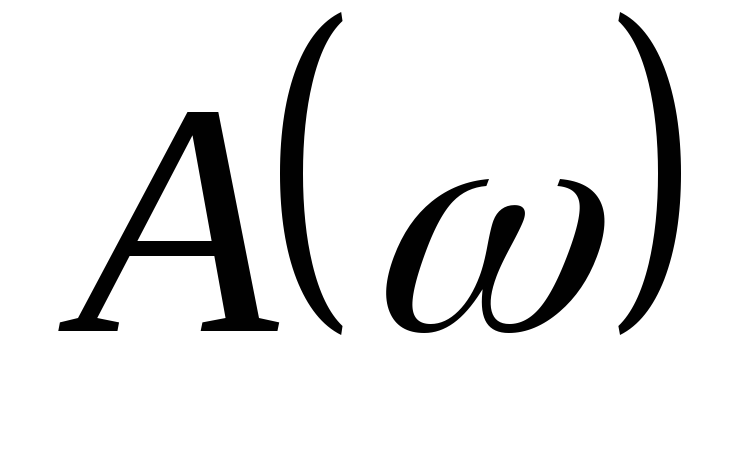 -
это кривая
изменения отношения
амплитуд выходной и входной величин в
зависимости от частоты
-
это кривая
изменения отношения
амплитуд выходной и входной величин в
зависимости от частоты
 (рис.3). Она показывает, как пропускает
САУ сигнал различной частоты. АЧХ
соответствует выражение (8).
(рис.3). Она показывает, как пропускает
САУ сигнал различной частоты. АЧХ
соответствует выражение (8).Фазовая частотная характеристика (ФЧХ)
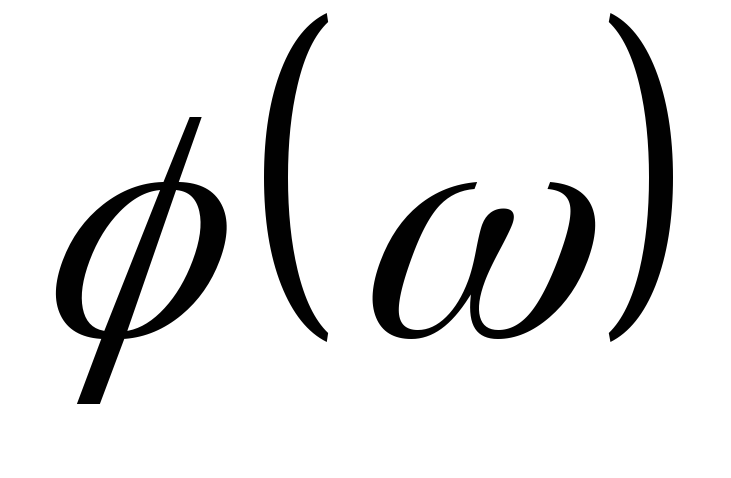 - это кривая изменения сдвига фаз
выходной величины по отношению к входной
в зависимости от частоты
- это кривая изменения сдвига фаз
выходной величины по отношению к входной
в зависимости от частоты
 (рис.4). Она показывает фазовые сдвиги,
вносимые САУ на различных частотах.
ФЧХ соответствует выражение (9).
(рис.4). Она показывает фазовые сдвиги,
вносимые САУ на различных частотах.
ФЧХ соответствует выражение (9).Вещественная частотная характеристика (ВЧК)
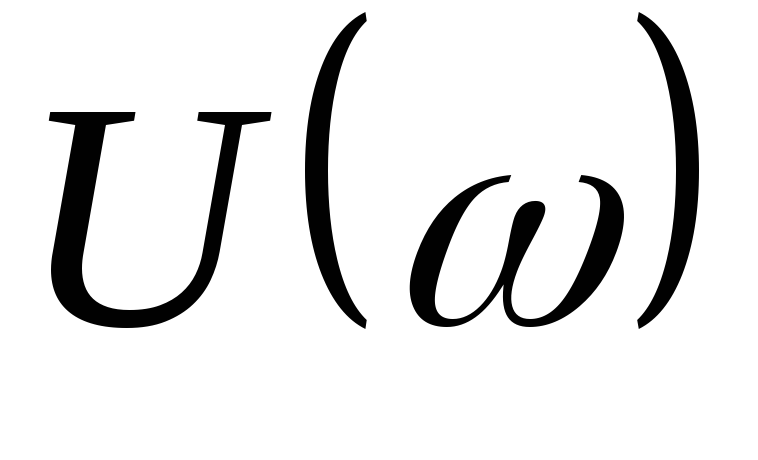 - это кривая, которой соответствует
вещественная составляющая ЧПФ (рис.5)
и выражение (6).
- это кривая, которой соответствует
вещественная составляющая ЧПФ (рис.5)
и выражение (6).Мнимая частотная характеристика (МЧХ)
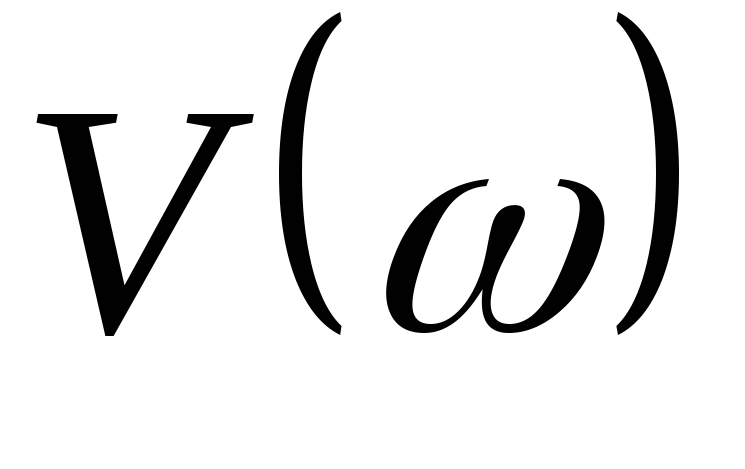 - это кривая, которой
соответствует
мнимая составляющая ЧПФ (рис.6) и выражение
(7).
- это кривая, которой
соответствует
мнимая составляющая ЧПФ (рис.6) и выражение
(7).
|
|
|
|
Рис.5. Вещественная частотная характеристика – ВЧХ |
Рис.6. Мнимая частотная характеристика – МЧХ |
Кривые АФЧХ, ФЧХ,
ВЧХ, МЧХ обладают свойством симметрии.
Поэтому по результатам вычисления
кривых для положительных частот можно
построить кривые для всего диапазона
частот
![]() ,
так как
,
так как
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
В связи с этим исследование звеньев
(систем) можно проводить только в
положительном диапазоне частот, тем
более, что отрицательные частоты реально
не существуют.
.
В связи с этим исследование звеньев
(систем) можно проводить только в
положительном диапазоне частот, тем
более, что отрицательные частоты реально
не существуют.
Исследование САУ значительно упрощается при использовании логарифмических частотных характеристик.
Логарифмическая
амплитудная частотная характеристика
(ЛАЧХ)
![]() – это кривая
(рис.7), построенная в логарифмическом
масштабе
частот
в соответствии с выражением:
– это кривая
(рис.7), построенная в логарифмическом
масштабе
частот
в соответствии с выражением:
|
|
(10) |
Единицей измерения
величины
![]() ,
которая
откладывается по оси ординат, является
децибел. По оси абсцисс откладывается
частота
,
которая
откладывается по оси ординат, является
децибел. По оси абсцисс откладывается
частота
![]() в логарифмическом масштабе
в логарифмическом масштабе
![]() .
Равномерной единицей по оси абсцисс
является декада – это любой отрезок,
на котором значение частоты увеличивается
в 10 раз.
.
Равномерной единицей по оси абсцисс
является декада – это любой отрезок,
на котором значение частоты увеличивается
в 10 раз.
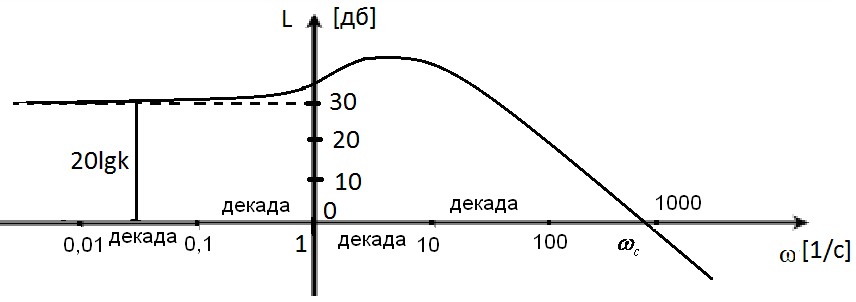
Рис.7. Логарифмическая амплитудная частотная характеристика.
Точка пересечения
ЛАЧХ с осью абсцисс называется частотой
среза
![]() .
Она определяется из условия
.
Она определяется из условия
|
|
(11) |
Ось
абсцисс (![]() )
соответствует значению
)
соответствует значению
![]() =l,
т.е. прохождению амплитуды сигнала через
САУ без изменения. Верхняя полуплоскость
ЛАЧХ соответствует значениям
=l,
т.е. прохождению амплитуды сигнала через
САУ без изменения. Верхняя полуплоскость
ЛАЧХ соответствует значениям
![]() ,
т.е. усилению амплитуды, а нижняя
полуплоскость – значениям
,
т.е. усилению амплитуды, а нижняя
полуплоскость – значениям
![]() ,
т.е. ослаблению амплитуды. ЛАЧХ может
быть приближенно построена в виде
асимптотической
ЛАЧХ,
представляющей собой совокупность
отрезков прямых линий (асимптот) с
наклонами, кратными величине 20 дб/дек.
,
т.е. ослаблению амплитуды. ЛАЧХ может
быть приближенно построена в виде
асимптотической
ЛАЧХ,
представляющей собой совокупность
отрезков прямых линий (асимптот) с
наклонами, кратными величине 20 дб/дек.
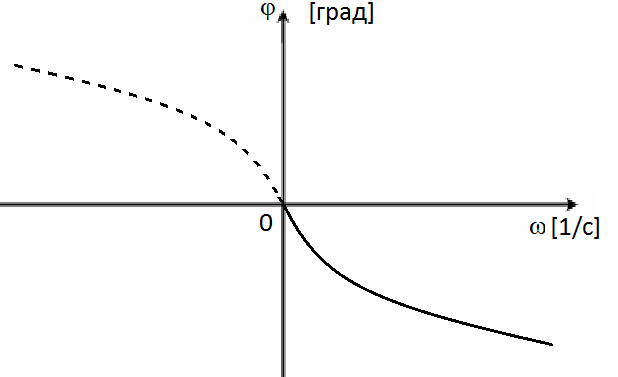
Логарифмическая
фазовая частотная характеристика (ЛФЧХ)
- это кривая ФЧХ
![]() ,
построенная в логарифмическом масштабе
частот (рис.8). Как и при построении ЛАЧХ
по оси абсцисс откладывают значение
частоты
,
построенная в логарифмическом масштабе
частот (рис.8). Как и при построении ЛАЧХ
по оси абсцисс откладывают значение
частоты
![]() в логарифмическом масштабе
в логарифмическом масштабе
![]() ,
а записывают действительное значение
частоты. По оси ординат откладывают
значении функции
,
а записывают действительное значение
частоты. По оси ординат откладывают
значении функции
![]() .
Таким образом, ЛФЧХ – это зависимость
.
Таким образом, ЛФЧХ – это зависимость
![]() от логарифма частоты
от логарифма частоты![]() .
.
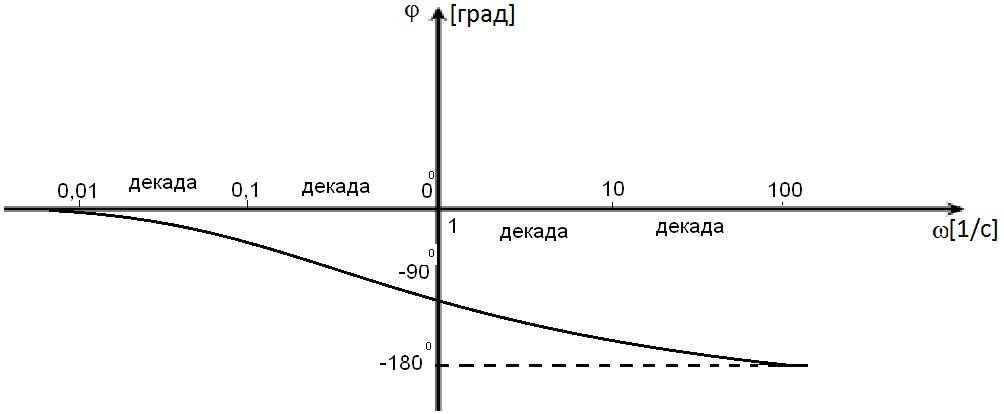
Рис.8. Логарифмическая фазовая частотная характеристика.
Для исследования замкнутой системы с передаточной функцией
|
|
(12) |
используются понятия, формулы и характеристики, аналогичные тем, что рассмотрены выше для разомкнутой системы.